中职数学高教版（2021）拓展模块二 下册第6章 三角计算6.4 解三角形6.4.3 余弦定理课文内容ppt课件

这是一份中职数学高教版（2021）拓展模块二 下册第6章 三角计算6.4 解三角形6.4.3 余弦定理课文内容ppt课件，共27页。PPT课件主要包含了教学目标，教学重难点，情境2，还有其他推导方式吗，余弦定理，同理得，余弦定理的变形，小组合作等内容，欢迎下载使用。
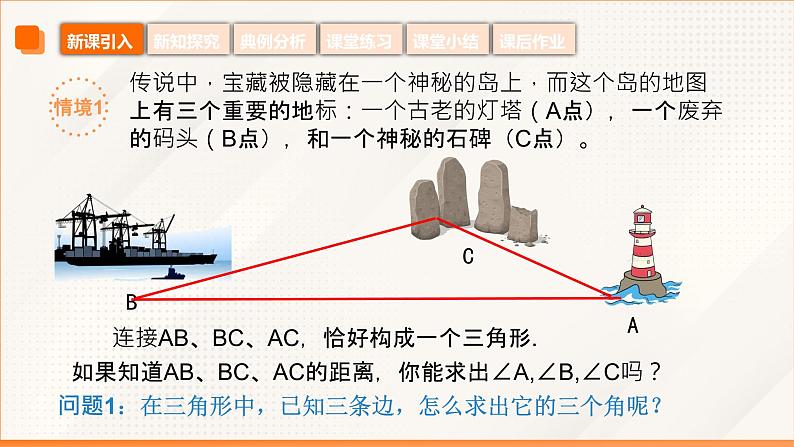
传说中，宝藏被隐藏在一个神秘的岛上，而这个岛的地图上有三个重要的地标：一个古老的灯塔（A点），一个废弃的码头（B点），和一个神秘的石碑（C点）。
连接AB、BC、AC，恰好构成一个三角形.
如果知道AB、BC、AC的距离，你能求出∠A,∠B,∠C吗？
问题1：在三角形中，已知三条边，怎么求出它的三个角呢？
园林工人在修建花圃的过程中，需在墙角的对面建造一道篱笆墙，问所建篱笆墙的长度为多少(不考虑其他因素)？
问题2：在三角形中，已知两边及其夹角，怎么求出此角的对边？
如图所示，以ΔABC的顶点A为坐标原点、射线AB的方向为x轴的正方向，建立平面直角坐标系，则点A、B的坐标分别为 A(0，0)，B(c，0)．
根据两点间距离公式可得，
即 a²=b²+c²-2bccsA.
同理得，b²=a²+c²-2accsB ， c²=a²+b²-2abcsC．
对任意三角形，这个定理是否都成立吗？
在∆ABC中，作CD⊥AB于点D
可以证明，对于任意三角形上述结论都成立.
三角形中任意一边的平方等于其余两边的平方和减这两边与其夹角余弦乘积的两倍.
观察余弦定理公式的结构特征，辅助记忆。另外，公式中共有四个变量,我们可以知三求一，利用余弦定理可以解决“在三角形中，已知两边及其夹角，求其他元素”的问题.
如何利用三角形三条边长求解三角形内角的角度大小？
用余弦定理判断三角形的类型
在△ABC中，a=4，b=6，∠C=60°，求c ．
由于a＜b＜c，故∠C最大．
因为0°＜∠C＜180° ，所以∠C=120° ．
我们可以知三求一，利用余弦定理可以解决“在三角形中，已知两边及其夹角，求其他元素”的问题.