




所属成套资源:中考数学一轮复习真题分点训练 (2份,原卷版+解析版)
中考数学一轮复习真题分点训练第二十二讲 与圆有关的计算(2份,原卷版+解析版)
展开
这是一份中考数学一轮复习真题分点训练第二十二讲 与圆有关的计算(2份,原卷版+解析版),文件包含中考数学一轮复习真题分点训练第二十二讲与圆有关的计算原卷版doc、中考数学一轮复习真题分点训练第二十二讲与圆有关的计算解析版doc等2份试卷配套教学资源,其中试卷共26页, 欢迎下载使用。
类型一 弧长的计算
1.(2022•丹东)如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠A=30°,则的长为( )
A.6πB.2πC.πD.π
【答案】D
【解答】解:∵直径AB=6,
∴半径OB=3,
∵圆周角∠A=30°,
∴圆心角∠BOC=2∠A=60°,
∴的长是=π,
故选:D.
2.(2022•广西)如图,在△ABC中,CA=CB=4,∠BAC=α,将△ABC绕点A逆时针旋转2α,得到△AB′C′,连接B′C并延长交AB于点D,当B′D⊥AB时,的长是( )
A.πB.πC.πD.π
【答案】B
【解答】解:∵CA=CB,CD⊥AB,
∴AD=DB=AB′.
∴∠AB′D=30°,
∴α=30°,
∵AC=4,
∴AD=AC•cs30°=4×=2,
∴,
∴的长度l==π.
故选:B.
3.(2022•甘肃)如图,一条公路(公路的宽度忽略不计)的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,半径OA=90m,圆心角∠AOB=80°,则这段弯路()的长度为( )
A.20πmB.30πmC.40πmD.50πm
【答案】C
【解答】解:∵半径OA=90m,圆心角∠AOB=80°,
∴这段弯路()的长度为:=40π(m),
故选:C.
类型二 扇形面积的计算
4.(2022•湖北)一个扇形的弧长是10πcm,其圆心角是150°,此扇形的面积为( )
A.30πcm2B.60πcm2C.120πcm2D.180πcm2
【答案】B
【解答】解:根据题意可得,
设扇形的半径为rcm,
则l=,
即10π=,
解得:r=12,
∴S===60π(cm2).
故选:B.
5.(2021•柳州)如图所示,点A,B,C对应的刻度分别为1,3,5,将线段CA绕点C按顺时针方向旋转,当点A首次落在矩形BCDE的边BE上时,记为点A′,则此时线段CA扫过的图形的面积为( )
A.4B.6C.D.
【答案】D
【解答】解:由题意,知AC=4,BC=4﹣2=2,∠A′BC=90°.
由旋转的性质,得A′C=AC=4.
在Rt△A′BC中,cs∠ACA′==.
∴∠ACA′=60°.
∴扇形ACA′的面积为=π.
即线段CA扫过的图形的面积为π.
故选:D.
命题点2 与扇形有关的阴影部分面积计算
类型一 直接和差法
6.(2022•贵港)如图,在▱ABCD中,AD=AB,∠BAD=45°,以点A为圆心、AD为半径画弧交AB于点E,连接CE,若AB=3,则图中阴影部分的面积是 .
【答案】 5﹣π
【解答】解:过点D作DF⊥AB于点F,
∵AD=AB,∠BAD=45°,AB=3,
∴AD=×3=2,
∴DF=ADsin45°=2×=2,
∵AE=AD=2,
∴EB=AB−AE=,
∴S阴影=S▱ABCD−S扇形ADE−S△EBC
=3×2﹣﹣××2
=5﹣π,
故答案为:5﹣π.
7.(2022•河南)如图,将扇形AOB沿OB方向平移,使点O移到OB的中点O′处,得到扇形A′O′B′.若∠O=90°,OA=2,则阴影部分的面积为 .
【答案】+
【解答】解:如图,设O′A′交于点T,连接OT.
∵OT=OB,OO′=O′B,
∴OT=2OO′,
∵∠OO′T=90°,
∴∠O′TO=30°,∠TOO′=60°,
∴S阴=S扇形O′A′B′﹣(S扇形OTB﹣S△OTO′)
=﹣(﹣×1×)
=+.
故答案为:+.
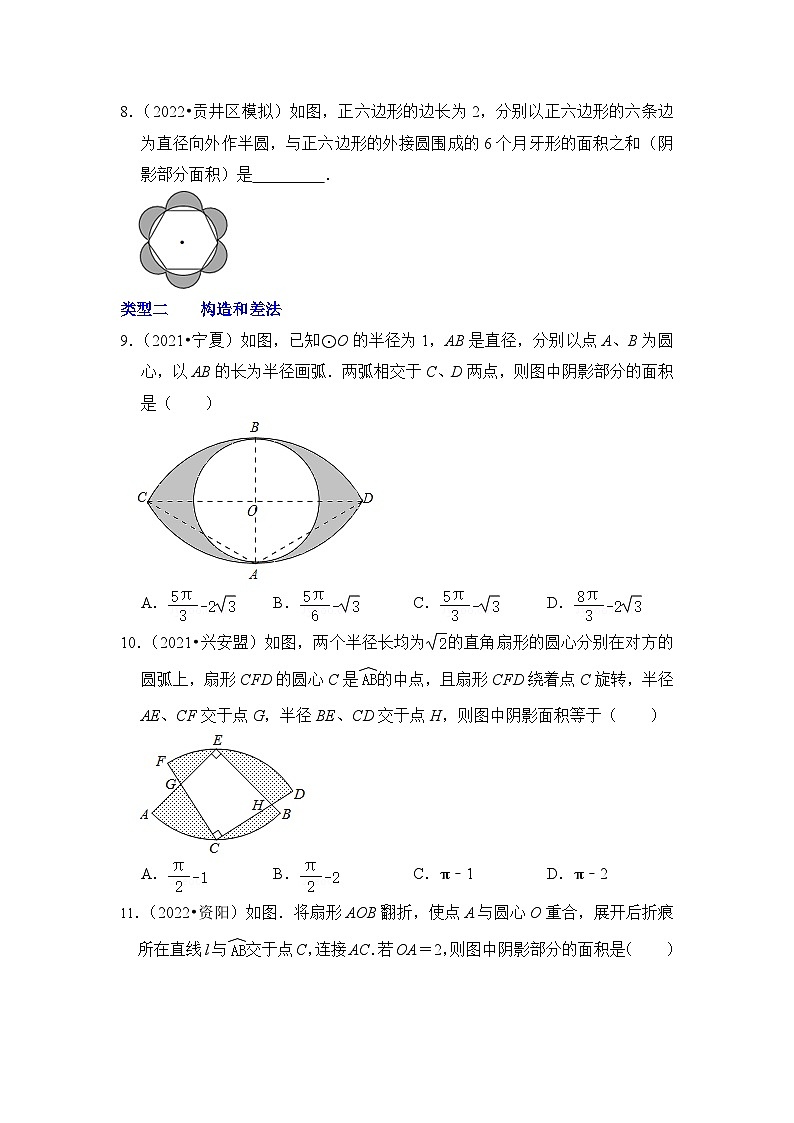
8.(2022•贡井区模拟)如图,正六边形的边长为2,分别以正六边形的六条边为直径向外作半圆,与正六边形的外接圆围成的6个月牙形的面积之和(阴影部分面积)是 .
【答案】(6﹣π)
【解答】解:6个月牙形的面积之和=3π﹣(22π﹣6××2×)=6﹣π,
故答案为:6﹣π.
类型二 构造和差法
9.(2021•宁夏)如图,已知⊙O的半径为1,AB是直径,分别以点A、B为圆心,以AB的长为半径画弧.两弧相交于C、D两点,则图中阴影部分的面积是( )
A.B.C.D.
【答案】A
【解答】解:连接BC,如图,
由作法可知AC=BC=AB=2,
∴△ACB为等边三角形,
∴∠BAC=60°,
∴S弓形BC=S扇形BAC﹣S△ABC,
∴图中阴影部分的面积=4S弓形BC+2S△ABC﹣S⊙O
=4(S扇形BAC﹣S△ABC)+2S△ABC﹣S⊙O
=4S扇形BAC﹣2S△ABC﹣S⊙O
=4×﹣2××22﹣π×12
=π﹣2.
故选:A.
10.(2021•兴安盟)如图,两个半径长均为的直角扇形的圆心分别在对方的圆弧上,扇形CFD的圆心C是的中点,且扇形CFD绕着点C旋转,半径AE、CF交于点G,半径BE、CD交于点H,则图中阴影面积等于( )
A.B.C.π﹣1D.π﹣2
【答案】D
【解答】解:两扇形的面积和为:=π,
过点C作CM⊥AE,作CN⊥BE,垂足分别为M、N,
则四边形EMCN是矩形,
∵点C是的中点,
∴EC平分∠AEB,
∴CM=CN,
∴矩形EMCN是正方形,
∵∠MCG+∠FCN=90°,∠NCH+∠FCN=90°,
∴∠MCG=∠NCH,
在△CMG与△CNH中,
,
∴△CMG≌△CNH(ASA),
∴中间空白区域面积相当于对角线是的正方形面积,
∴空白区域的面积为:××=1,
∴图中阴影部分的面积=两个扇形面积和﹣2个空白区域面积的和=π﹣2.
故选:D.
11.(2022•资阳)如图.将扇形AOB翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接AC.若OA=2,则图中阴影部分的面积是( )
A.B.C.D.
【答案】B
【解答】解:连接CO,直线l与AO交于点D,如图所示,
∵扇形AOB中,OA=2,
∴OC=OA=2,
∵点A与圆心O重合,
∴AD=OD=1,CD⊥AO,
∴OC=AC,
∴OA=OC=AC=2,
∴△OAC是等边三角形,
∴∠COD=60°,
∵CD⊥OA,
∴CD===,
∴阴影部分的面积为:=﹣,
故选:B.
12.(2022•赤峰)如图,AB是⊙O的直径,将弦AC绕点A顺时针旋转30°得到AD,此时点C的对应点D落在AB上,延长CD,交⊙O于点E,若CE=4,则图中阴影部分的面积为( )
A.2πB.2C.2π﹣4D.2π﹣2
【答案】C
【解答】解:连接OE,OC,BC,
由旋转知AC=AD,∠CAD=30°,
∴∠BOC=60°,∠ACE=(180°﹣30°)÷2=75°,
∴∠BCE=90°﹣∠ACE=15°,
∴∠BOE=2∠BCE=30°,
∴∠EOC=90°,
即△EOC为等腰直角三角形,
∵CE=4,
∴OE=OC=2,
∴S阴影=S扇形OEC﹣S△OEC=﹣×=2π﹣4,
故选:C.
类型三 等积转化法
13.(2021•泰安)若△ABC为直角三角形,AC=BC=4,以BC为直径画半圆如图所示,则阴影部分的面积为 .
【答案】4
【解答】解:设AB交半圆于点D,连接CD.
∵BC是直径,
∴∠BDC=90°,即CD⊥AB;
又∵△ABC为等腰直角三角形,
∴CD垂直平分斜边AB,
∴CD=BD=AD,
∴=,
∴S弓形BD=S弓形CD,
∴S阴影=SRt△ABC﹣SRt△BCD;
∵△ABC为等腰直角三角形,CD是斜边AB的垂直平分线,
∴SRt△ABC=2SRt△BCD;
又SRt△ABC=×4×4=8,
∴S阴影=4;
故答案为:4.
14..(2020•朝阳)如图,点A,B,C是⊙O上的点,连接AB,AC,BC,且∠ACB=15°,过点O作OD∥AB交⊙O于点D,连接AD,BD,已知⊙O半径为2,则图中阴影面积为 .
【答案】
【解答】解:∵∠ACB=15°,
∴∠AOB=30°,
∵OD∥AB,
∴S△ABD=S△ABO,
∴S阴影=S扇形AOB=.
故答案为:.
命题点3 圆切线与阴影部分求面积结合
15.(2021•扬州)如图,四边形ABCD中,AD∥BC,∠BAD=90°,CB=CD,连接BD,以点B为圆心,BA长为半径作⊙B,交BD于点E.
(1)试判断CD与⊙B的位置关系,并说明理由;
(2)若AB=2,∠BCD=60°,求图中阴影部分的面积.
【答案】(1) CD与⊙B相切 (2)
【解答】解:(1)过点B作BF⊥CD,垂足为F,
∵AD∥BC,
∴∠ADB=∠CBD,
∵CB=CD,
∴∠CBD=∠CDB,
∴∠ADB=∠CDB.
在△ABD和△FBD中,
,
∴△ABD≌△FBD(AAS),
∴BF=BA,则点F在圆B上,
∴CD与⊙B相切;
(2)∵∠BCD=60°,CB=CD,
∴△BCD是等边三角形,
∴∠CBD=60°
∵BF⊥CD,
∴∠ABD=∠DBF=∠CBF=30°,
∴∠ABF=60°,
∵AB=BF=,
∴AD=DF=AB·tan30°=2,
∴阴影部分的面积=S△ABD﹣S扇形ABE
=
=.
命题点4 圆锥、圆柱的相关计算
16.(2022•东营)用一张半圆形铁皮,围成一个底面半径为4cm的圆锥形工件的侧面(接缝忽略不计),则圆锥的母线长为( )
A.4cmB.8cmC.12cmD.16cm
【答案】B
【解答】解:设半圆形铁皮的半径为rcm,
根据题意得:πr=2π×4,
解得:r=8,
所以围成的圆锥的母线长为8cm,
故选:B.
17.2022•济宁)已知圆锥的母线长8cm,底面圆的直径6cm,则这个圆锥的侧面积是( )
A.96πcm2B.48πcm2C.33πcm2D.24πcm2
【答案】D
【解答】解:∵底面圆的直径为6cm,
∴底面圆的半径为3cm,
∴圆锥的侧面积=×8×2π×3=24πcm2.
故选:D.
18.(2022•牡丹江)圆锥的底面圆半径是1,母线长是3,它的侧面展开图的圆心角是( )
A.90°B.100°C.120°D.150°
【答案】C
【解答】解:圆锥侧面展开图的弧长是:2π×1=2π,
设圆心角的度数是n度.
则=2π,
解得:n=120.
故选:C.
19.(2022•广安)蒙古包可以近似地看作由圆锥和圆柱组成.下图是一个蒙古包的示意图,底面圆半径DE=2m,圆锥的高AC=1.5m,圆柱的高CD=2.5m,则下列说法错误的是( )
A.圆柱的底面积为4πm2
B.圆柱的侧面积为10πm2
C.圆锥的母线AB长为2.25m
D.圆锥的侧面积为5πm2
【答案】C
【解答】解:∵底面圆半径DE=2m,
∴圆柱的底面积为4πm2,所以A选项不符合题意;
∵圆柱的高CD=2.5m,
∴圆柱的侧面积=2π×2×2.5=10π(m2),所以B选项不符合题意;
∵底面圆半径DE=2m,即BC=2m,圆锥的高AC=1.5m,
∴圆锥的母线长AB==2.5(m),所以C选项符合题意;
∴圆锥的侧面积=×2π×2×2.5=5π(m2),所以D选项不符合题意.
故选:C.
20.(2021•广西)如图,从一块边长为2,∠A=120°的菱形铁片上剪出一个扇形,这个扇形在以A为圆心的圆上(阴影部分),且圆弧与BC,CD分别相切于点E,F,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径是 .
【答案】
【解答】解:连接AC、AE,如图,
∵四边形ABCD为菱形,
∴∠BAC=∠BAD=×120°=60°,AB=BC,
∴△ABC为等边三角形,
∵圆弧与BC相切于E,
∴AE⊥BC,
∴BE=CE=1,
∴AE===,
设圆锥的底面圆半径为r,
根据题意得2πr=,解得r=,
即圆锥的底面圆半径为.
故答案为.
命题点5 圆与正多边形的相关计算
21.(2022•绵阳)在2022年北京冬奥会开幕式和闭幕式中,一片“雪花”的故事展现了“世界大同、天下一家”的主题,让世界观众感受了中国人的浪漫.如图,将“雪花”图案(边长为4的正六边形ABCDEF)放在平面直角坐标系中,若AB与x轴垂直,顶点A的坐标为(2,﹣3),则顶点C的坐标为( )
A.(2﹣2,3)B.(0,1+2)C.(2﹣,3)D.(2﹣2,2+)
【答案】A
【解答】解:如图,连接BD交CF于点M,则点B(2,1),
在Rt△BCM中,BC=4,∠BCM=×120°=60°,
∴CM=BC=2,BM=BC=2,
∴点C的横坐标为﹣(2﹣2)=2﹣2,纵坐标为1+2=3,
∴点C的坐标为(2﹣2,3),
故选:A.
22.(2022•雅安)如图,已知⊙O的周长等于6π,则该圆内接正六边形ABCDEF的边心距OG为( )
A.3B.C.D.3
【答案】C
【解答】解:连接OC,OD,
∵正六边形ABCDEF是圆的内接多边形,
∴∠COD=60°,
∵OC=OD,OG⊥CD,
∴∠COG=30°,
∵⊙O的周长等于6π,
∴OC=3,
∴OG=3cs30°=,
故选:C.
相关试卷
这是一份中考数学一轮复习知识梳理+考点精讲专题27 与圆有关的计算(2份,原卷版+解析版),文件包含中考数学一轮复习知识梳理+考点精讲专题27与圆有关的计算原卷版doc、中考数学一轮复习知识梳理+考点精讲专题27与圆有关的计算解析版doc等2份试卷配套教学资源,其中试卷共35页, 欢迎下载使用。
这是一份中考数学一轮复习题型归纳训练专题16 与圆有关的计算(2份,原卷版+解析版),文件包含中考数学一轮复习题型归纳训练专题16与圆有关的计算原卷版doc、中考数学一轮复习题型归纳训练专题16与圆有关的计算解析版doc等2份试卷配套教学资源,其中试卷共42页, 欢迎下载使用。
这是一份中考数学第一轮专题复习真题分点透练(全国通用)第二十二讲与圆有关的计算(原卷版+解析),共23页。试卷主要包含了是 等内容,欢迎下载使用。








