2025年中考数学一轮复习分层精练专题24 正方形的性质与判定（2份，原卷版+解析版）

这是一份2025年中考数学一轮复习分层精练专题24 正方形的性质与判定（2份，原卷版+解析版），文件包含2025年中考数学一轮复习分层精练专题24正方形的性质与判定原卷版doc、2025年中考数学一轮复习分层精练专题24正方形的性质与判定解析版doc等2份试卷配套教学资源，其中试卷共25页， 欢迎下载使用。

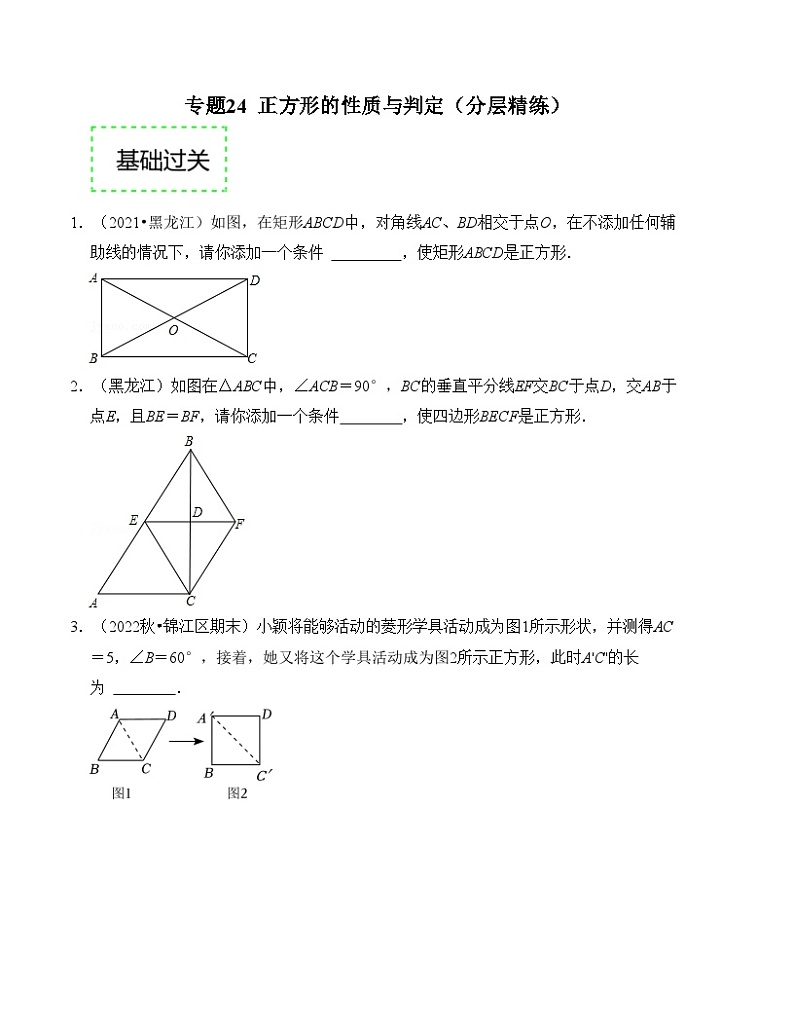
1．（2021•黑龙江）如图，在矩形ABCD中，对角线AC、BD相交于点O，在不添加任何辅助线的情况下，请你添加一个条件 ，使矩形ABCD是正方形．
【答案】 AB＝AD（或AC⊥BD答案不唯一）
【解答】解：AB＝AD（或AC⊥BD答案不唯一）．
理由：∵四边形ABCD是矩形，
又∵AB＝AD，
∴四边形ABCD是正方形．
或∵四边形ABCD是矩形，
又∵AC⊥BD，
∴四边形ABCD是正方形，
故答案为：AB＝AD（或AC⊥BD答案不唯一）．
2．（黑龙江）如图在△ABC中，∠ACB＝90°，BC的垂直平分线EF交BC于点D，交AB于点E，且BE＝BF，请你添加一个条件 ，使四边形BECF是正方形．
【答案】AC＝BC
【解答】解：添加条件：AC＝BC．理由如下：
∵EF垂直平分BC，
∴BE＝EC，BF＝CF，
∵BF＝BE，
∴BE＝EC＝CF＝BF，
∴四边形BECF是菱形；
当BC＝AC时，
∵∠ACB＝90°，
则∠A＝45°时，菱形BECF是正方形．
∵∠A＝45°，∠ACB＝90°，
∴∠EBC＝45°
∴∠EBF＝2∠EBC＝2×45°＝90°
∴菱形BECF是正方形．
故答案为AC＝BC．
3．（2022秋•锦江区期末）小颖将能够活动的菱形学具活动成为图1所示形状，并测得AC＝5，∠B＝60°，接着，她又将这个学具活动成为图2所示正方形，此时A'C'的长为 ．
【答案】5
【解答】解：∵四边形ABCD是菱形，
∴AB＝BC，
∵∠B＝60°，
∴△ABC是等边三角形，
∴AB＝BC＝AC，
∵AC＝5，
∴AB＝BC＝5，
∵四边形A′B′C′D′为正方形，
∴∠A′B′C′＝90°，
由旋转的性质得出A′B′＝B′C′＝AB＝5，
∴A′C′＝＝5，
故答案为：5．
4．（2020•呼伦贝尔）已知：如图，在正方形ABCD中，对角线AC，BD相交于点O，点E，F分别是边BC，CD上的点，且∠EOF＝90°．
求证：CE＝DF．
【解答】证明：∵四边形ABCD为正方形，
∴OD＝OC，∠ODF＝∠OCE＝45°，∠COD＝90°，
∴∠DOF+∠COF＝90°，
∵∠EOF＝90°，即∠COE+∠COF＝90°，
∴∠COE＝∠DOF，
∴△COE≌△DOF（ASA），
∴CE＝DF．
5．（2020•西宁）如图，E是正方形ABCD对角线BD上一点，连接AE，CE，并延长CE交AD于点F．
（1）求证：△ABE≌△CBE；
（2）若∠AEC＝140°，求∠DFE的度数．
【解答】（1）证明：∵四边形ABCD是正方形，
∴AB＝CB，∠ABC＝∠ADC＝90°，，
在△ABE和△CBE中，
，
∴△ABE≌△CBE（SAS）；
（2）∵△ABE≌△CBE，
∴∠AEB＝∠CEB，
又∵∠AEC＝140°，
∴∠CEB＝70°，
∵∠DEC+∠CEB＝180°，
∴∠DEC＝180°﹣∠CEB＝110°，
∵∠DFE+∠ADB＝∠DEC，
∴∠DFE＝∠DEC﹣∠ADB＝110°﹣45°＝65°．
6．（2021•邵阳）如图，在正方形ABCD中，对角线AC，BD相交于点O，点E，F是对角线AC上的两点，且AE＝CF．连接DE，DF，BE，BF．
（1）证明：△ADE≌△CBF．
（2）若AB＝4，AE＝2，求四边形BEDF的周长．
【解答】（1）证明：由正方形对角线平分每一组对角可知：∠DAE＝∠BCF＝45°，
在△ADE和△CBF中，
，
∴△ADE≌△CBF（SAS）．
（2）解：∵AB＝AD＝，
∴BD＝＝＝8，
由正方形对角线相等且互相垂直平分可得：AC＝BD＝8，DO＝BO＝4，OA＝OC＝4，
又AE＝CF＝2，
∴OA﹣AE＝OC﹣CF，
即OE＝OF＝4﹣2＝2，
故四边形BEDF为平行四边形．
∵∠DOE＝90°，
∴四边形BEDF是菱形，
∴DE＝＝＝2．
∴4DE＝，
故四边形BEDF的周长为8．
7．（上海）已知：如图，四边形ABCD中，AD∥BC，AD＝CD，E是对角线BD上一点，且EA＝EC．
（1）求证：四边形ABCD是菱形；
（2）如果BE＝BC，且∠CBE：∠BCE＝2：3，求证：四边形ABCD是正方形．
【解答】证明：（1）在△ADE与△CDE中，
，
∴△ADE≌△CDE，
∴∠ADE＝∠CDE，
∵AD∥BC，
∴∠ADE＝∠CBD，
∴∠CDE＝∠CBD，
∴BC＝CD，
∵AD＝CD，
∴BC＝AD，
∴四边形ABCD为平行四边形，
∵AD＝CD，
∴四边形ABCD是菱形；
（2）∵BE＝BC
∴∠BCE＝∠BEC，
∵∠CBE：∠BCE＝2：3，
∴∠CBE＝180×＝45°，
∵四边形ABCD是菱形，
∴∠ABE＝45°，
∴∠ABC＝90°，
∴四边形ABCD是正方形
8．（2022•遵义）将正方形ABCD和菱形EFGH按照如图所示摆放，顶点D与顶点H重合，菱形EFGH的对角线HF经过点B，点E，G分别在AB，BC上．
（1）求证：△ADE≌△CDG；
（2）若AE＝BE＝2，求BF的长．
【解答】（1）证明：∵四边形ABCD是正方形，四边形HEFG是菱形，
∴AD＝CD，ED＝GD，∠A＝∠C＝90°，
在Rt△ADE和Rt△CDG中，
，
∴Rt△ADE≌Rt△CDG（HL）；
（2）解：过E作EQ⊥DF于Q，则∠EQB＝90°，
∵四边形ABCD是正方形，
∴∠A＝90°，AD＝AB＝AE+BE＝2+2＝4，∠EBQ＝∠CBD＝45°，
∴∠QEB＝45°＝∠EBQ，
∴EQ＝BQ，
∵BE＝2，
∴2EQ2＝22，
∴EQ＝BQ＝（负数舍去），
在Rt△DAE中，由勾股定理得：DE＝＝＝2，
∵四边形EFGH是菱形，
∴EF＝DE＝2，
∴QF＝＝＝3，
∴BF＝QF﹣QB＝3﹣＝2．
9．（2019•玉林）如图，在正方形ABCD中，分别过顶点B，D作BE∥DF交对角线AC所在直线于E，F点，并分别延长EB，FD到点H，G，使BH＝DG，连接EG，FH．
（1）求证：四边形EHFG是平行四边形；
（2）已知：AB＝2，EB＝4，tan∠GEH＝2，求四边形EHFG的周长．
【解答】解：（1）∵四边形ABCD是正方形，
∴AB＝CD，AB∥CD，
∴∠DCA＝∠BAC，
∵DF∥BE，
∴∠CFD＝∠BEA，
∵∠BAC＝∠BEA+∠ABE，∠DCA＝∠CFD+∠CDF，
∴∠ABE＝∠CDF，
在△ABE和△CDF中，
∵，
∴△ABE≌△CDF（AAS），
∴BE＝DF，
∵BH＝DG，
∴BE+BH＝DF+DG，
即EH＝GF，
∵EH∥GF，
∴四边形EHFG是平行四边形；
（2）如图，连接BD，交EF于O，
∵四边形ABCD是正方形，
∴BD⊥AC，
∴∠AOB＝90°，
∵AB＝2，
∴OA＝OB＝2，
Rt△BOE中，EB＝4，
∴∠OEB＝30°，
∴EO＝2，
∵OD＝OB，∠EOB＝∠DOF，
∵DF∥EB，
∴∠DFC＝∠BEA，
∴△DOF≌△BOE（AAS），
∴OF＝OE＝2，
∴EF＝4，
∴FM＝2，EM＝6，
过F作FM⊥EH于M，交EH的延长线于M，
∵EG∥FH，
∴∠FHM＝∠GEH，
∵tan∠GEH＝tan∠FHM＝＝2，
∴，
∴HM＝1，
∴EH＝EM﹣HM＝6﹣1＝5，FH＝＝＝，
∴四边形EHFG的周长＝2EH+2FH＝2×5+2＝10+2．
10．（2021•牡丹江）如图1，四边形ABCD是正方形，点E是边BC的中点，∠AEF＝90°，且EF交正方形外角的平分线CF于点F，过点F作FG⊥BC于点G，连接AC．易证：AC＝（EC+FG）．（提示：取AB的中点M，连接EM）
（1）当点E是BC边上任意一点时，如图2；当点E在BC延长线上时，如图3．请直接写出AC，EC，FG的数量关系，并对图2进行证明；
（2）已知正方形ABCD的面积是27，连接AF，当△ABE中有一个内角为30°时，则AF的长为 ．
【解答】解：（1）如图2中，结论：AC＝（FG+EC）．
理由：在AB上截取BM＝BE，连接EM，
∵四边形ABCD是正方形，
∴∠B＝∠BCD＝90°，AB＝BC，
∴∠DCG＝90°，∠EAM+∠AEB＝90°，
∵BM＝BE，
∴AB﹣BM＝BC﹣BE，∠BME＝∠BEM＝45°，
∴AM＝EC，∠AME＝135°，
∵CF平分∠DCG，
∴∠FCG＝45°，
∴∠ECF＝135°，
∴∠AME＝∠ECF，
∵∠AEF＝90°，
∴∠FEC+∠AEB＝90°，
∴∠EAM＝∠FEC，
∴在△AEM和△EFC中，
，
∴△AEM≌△EFC（ASA），
∴EM＝CF，
∵EM＝BE，CF＝FG，
∴BE＝FG，
∵AC＝BC＝（BE+EC），
∴AC＝（FG+EC）．
如图3中，结论：AC＝（FG﹣EC）．
（2）如图1中，当∠BAE＝30°时，
∵正方形的面积为27，
∴AB＝3，∠B＝90°，
∴BE＝AB•tan30°＝3×＝3，
∴AE＝2BE＝6，
∵△AEM≌△EFC
∴AE＝EF＝6，
∴AF＝6，
如图3中，当∠AEB＝30°时，同法可得AE＝EF＝2AB＝6，
∴AF＝AE＝6，
综上所述，AF的长为6或6．
11．（2022•大庆三模）如图，已知四边形ABCD为正方形AB＝2，点E为对角线AC上一点，连接DE，过点E作EF⊥DE，交BC延长线于点F，以DE、EF为邻边作矩形DEFG，连接CG．在下列结论中：①矩形DEFG是正方形； ②2CE+CG＝AD；③CG平分∠DCF；④CE＝CF．其中正确的结论有（ ）
A．①③B．②④C．①②③D．①②③④
【答案】A
【解答】解：过E作EM⊥BC于M点，过E作EN⊥CD于N点，如图所示：
∵四边形ABCD是正方形，
∴∠BCD＝90°，∠ECN＝45°，
∴∠EMC＝∠ENC＝∠BCD＝90°，
∴NE＝NC，
∴四边形EMCN为正方形，
∵四边形DEFG是矩形，
∴EM＝EN，∠DEN+∠NEF＝∠MEF+∠NEF＝90°，
∴∠DEN＝∠MEF，
又∠DNE＝∠FME＝90°，
在△DEN和△FEM中，
，
∴△DEN≌△FEM（ASA），
∴ED＝EF，
∴矩形DEFG为正方形；故①正确；
∴DE＝DG，∠EDC+∠CDG＝90°，
∵四边形ABCD是正方形，
∵AD＝DC，∠ADE+∠EDC＝90°，
∴∠ADE＝∠CDG，
在△ADE和△CDG中，
，
∴△ADE≌△CDG（SAS），
∴AE＝CG，∠DAE＝∠DCG＝45°，
∵∠DCF＝90°，
∴CG平分∠DCF，故③正确；
∴AC＝AE+CE＝CE+CG＝AD，故②错误；
当DE⊥AC时，点C与点F重合，
∴CE不一定等于CF，故④错误，
故选：A．
12．（2022•城关区校级模拟）如图，在正方形ABCD中，点P在对角线BD上，PE⊥BC，PF⊥CD，E，F分别为垂足，连结AP，EF，则下列命题：①若AP＝5，则EF＝5；②若AP⊥BD，则EF∥BD；③若正方形边长为4，则EF的最小值为2，其中正确的命题是（ ）
A．①②B．①③C．②③D．①②③
【答案】A
【解答】解：延长EP交AD于Q，
∵四边形ABCD为正方形，
∴AD＝CD，∠ADC＝∠C＝90°，AD∥BC，∠BDC＝45°，
∵PF⊥CD，
∴∠DPF＝45°，
∴DF＝PF，
∵PE⊥BC，
∴PQ⊥AD，四边形CEPF为矩形，
∴∠AQP＝90°，EC＝PF＝DF，
∴∠AQP＝∠C，AQ＝FC，四边形PQDF为正方形，
∴DF＝QP，
∴CE＝QP，
在△AQP和△FCE中，
，
∴△AQP≌△FCE（SAS），
∴AP＝EF，
若AP＝5，则EF＝5，故①正确；
若AP⊥BD，则∠PAQ＝45°，
∵△AQP≌△FCE，
∴∠EFC＝∠PAQ＝45°，
∵∠BDC＝45°，
∴∠EFC＝∠BDC，
∴EF∥BD，故②正确；
当AP⊥BD时，AP有最小值，此时P为BD的中点，
∵AB＝AD＝4，
∴BD＝，
∴AP＝BD＝，
∵EF＝AP，
∴EF的最小值为，故③错误，
故选：A．
13．（2022•泰安一模）如图，AD是△ABC的角平分线，DE，DF分别是△ABD和△ACD的高，得到下列四个结论：①OA＝OD；②AD⊥EF；③当∠A＝90°时，四边形AEDF是正方形；④AE+DF＝AF+DE．其中正确的是（ ）
A．②③B．②④C．①③④D．②③④
【答案】D
【解答】解：如果OA＝OD，则四边形AEDF是矩形，没有说∠A＝90°，不符合题意，故①错误；
∵AD是△ABC的角平分线，
∴∠EAD＝∠FAD，
在△AED和△AFD中，，
∴△AED≌△AFD（AAS），
∴AE＝AF，DE＝DF，
∴AE+DF＝AF+DE，故④正确；
∵在△AEO和△AFO中，，
∴△AEO≌△AFO（SAS），
∴EO＝FO，
又∵AE＝AF，
∴AO是EF的中垂线，
∴AD⊥EF，故②正确；
∵当∠A＝90°时，四边形AEDF的四个角都是直角，
∴四边形AEDF是矩形，
又∵DE＝DF，
∴四边形AEDF是正方形，故③正确．
综上可得：正确的是：②③④，
故选：D．