江西省吉安市八校联考2024-2025学年七年级上学期12月月考 数学试题（含解析）

这是一份江西省吉安市八校联考2024-2025学年七年级上学期12月月考 数学试题（含解析），共15页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
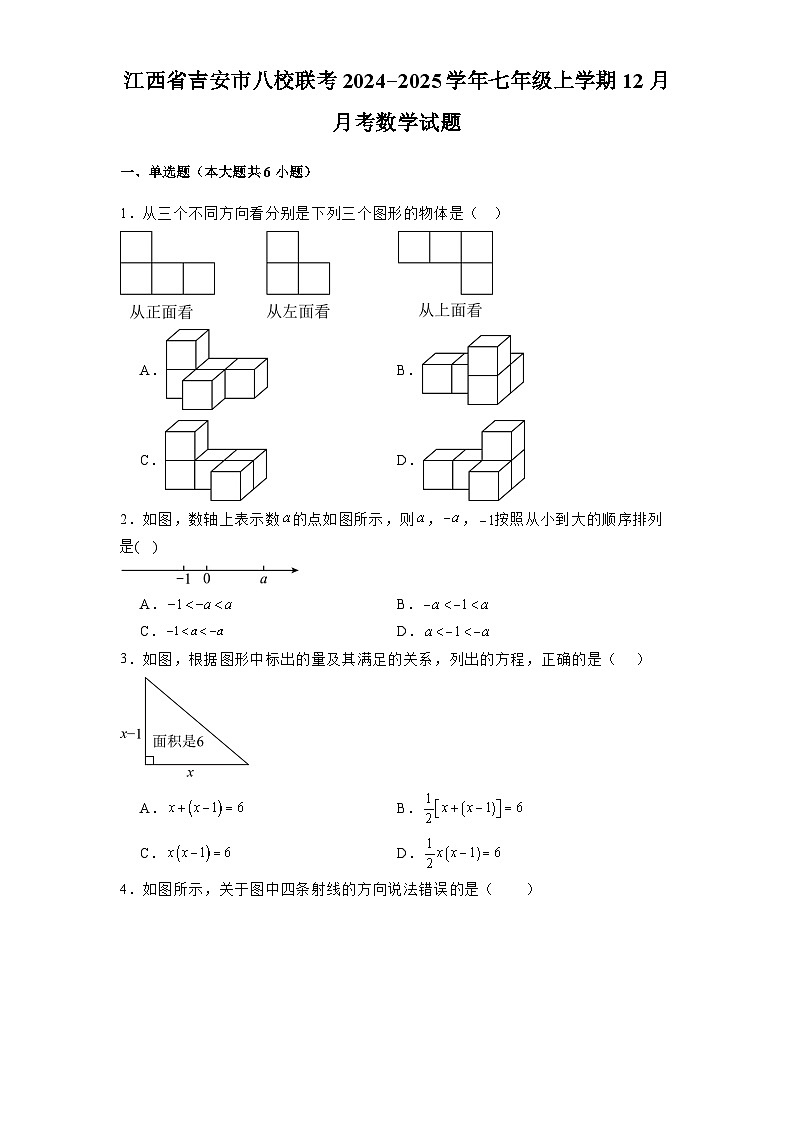
1．从三个不同方向看分别是下列三个图形的物体是（ ）
A．B．
C．D．
2．如图，数轴上表示数的点如图所示，则，，按照从小到大的顺序排列是( )
A．B．
C．D．
3．如图，根据图形中标出的量及其满足的关系，列出的方程，正确的是（ ）
A．B．
C．D．
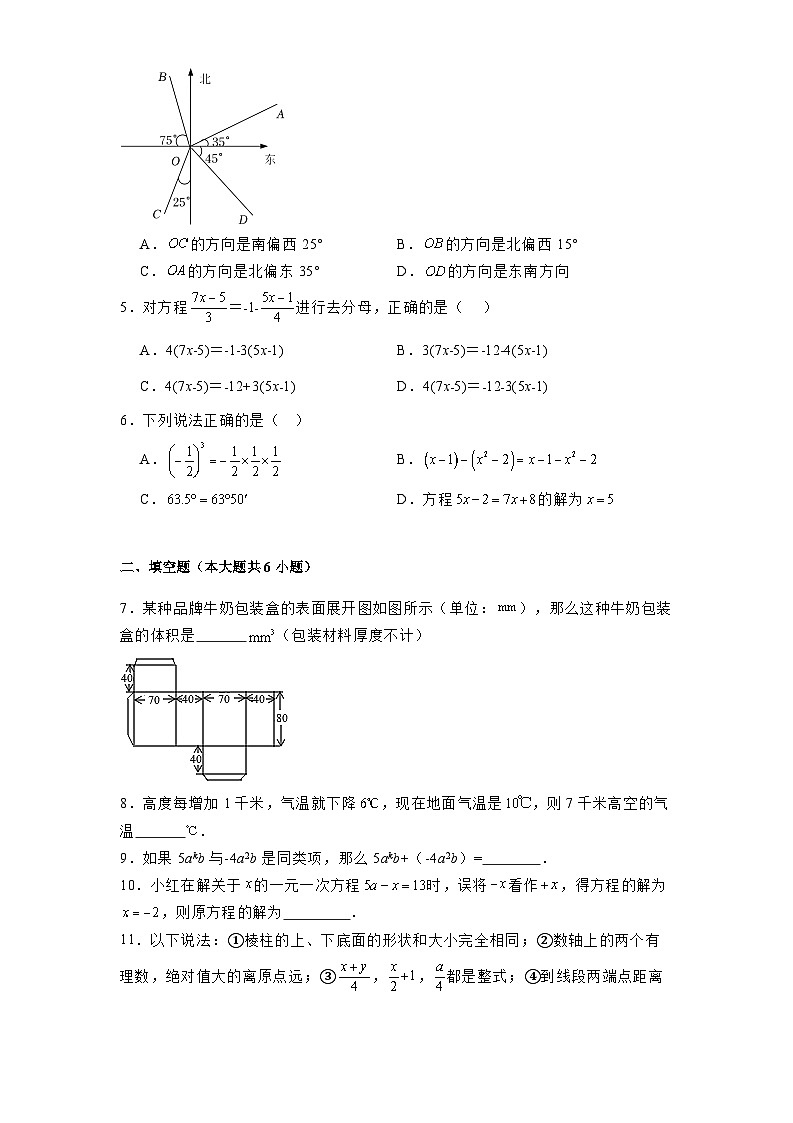
4．如图所示，关于图中四条射线的方向说法错误的是（ ）
A．的方向是南偏西25°B．的方向是北偏西15°
C．的方向是北偏东35°D．的方向是东南方向
5．对方程＝﹣1﹣进行去分母，正确的是（ ）
A．4(7x﹣5)＝﹣1﹣3(5x﹣1)B．3(7x﹣5)＝﹣12﹣4(5x﹣1)
C．4(7x﹣5)＝﹣12+3(5x﹣1)D．4(7x﹣5)＝﹣12﹣3(5x﹣1)
6．下列说法正确的是（ ）
A．B．
C．D．方程的解为
二、填空题（本大题共6小题）
7．某种品牌牛奶包装盒的表面展开图如图所示（单位：），那么这种牛奶包装盒的体积是 （包装材料厚度不计）
8．高度每增加1千米，气温就下降，现在地面气温是，则7千米高空的气温 ．
9．如果5akb与-4a2b是同类项，那么5akb+（-4a2b）= ．
10．小红在解关于的一元一次方程时，误将看作，得方程的解为，则原方程的解为 ．
11．以下说法：①棱柱的上、下底面的形状和大小完全相同；②数轴上的两个有理数，绝对值大的离原点远；③，，都是整式；④到线段两端点距离相等的点是线段的中点；⑤若，则．其中正确的是 ．（填序号）
12．如图，图中数轴的单位长度为．若原点为的四等分点，则点代表的数为 ．

三、解答题（本大题共11小题）
13．解决下面问题：
(1)计算；
(2)解方程．
14．补全解题过程．已知：如图，点是线段上一点，点是线段的中点，，．求线段AB的长度．
解：∵，（已知），∴_____________；
∵点是线段的中点（已知），∴____________（线段中点的定义）
∵，∴____________．
15．下面是小超解方程的过程．
按要求完成下面的问题：
(1)上述解方程第一步变形的依据是________；
(2)小超从第______步开始出现错误，请你完整写出正确的解答过程．
16．王先生到市行政中心大楼办事，假定乘电梯向上一楼记作，向下一楼记作，王先生从1楼出发，电梯上下楼层依次记录如下（单位：层）：．
(1)请你通过计算说明王先生最后是否回到出发点1楼；
(2)该中心大楼每层高，电梯每向上或下需要耗电度，根据王先生现在所处位置，请你算算，他办事时电梯需要耗电多少度？
17．已知有理数、、满足、、，且
(1)在数轴上将、、三个数填在相应的括号中．
(2)化简：．
18．如图，为线段上一点，为线段的中点．
(1)若，，求线段的长．
(2)延长到点，使．在图中完成作图，并写出图中所有相等的线段．（除外）
19．阅读材料：我们知道，，类似地，我们把看成一个整体，则．“整体思想”是中学教学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛．
尝试应用：
(1)把看成一个整体，合并的结果是______；
(2)已知，求的值；
拓广探索：
(3)已知，，，求的值．
20．如图，将一副直角三角板的直角顶点C叠放在一起．
（1）如图（1），若∠DCE＝33°，则∠BCD＝ ，∠ACB＝ ．
（2）如图（1），猜想∠ACB与∠DCE的大小有何特殊关系？并说明理由．
（3）如图（2），若是两个同样的直角三角板60°锐角的顶点A重合在一起，则∠DAB与∠CAE的数量关系为 ．
21．居民生活中使用天然气实行阶梯式计价，用户每月用气量在20立方米及以内的为第一级基数，按一级用气价格收取；超过20立方米且不超过30立方米的部分为第二级气量基数，按一级用气价格的1.5倍收取：超过30立方米的部分为第三级气量基数，按一级用气价格的1.8倍收取．为节约用气量，小明记录了1－7月份他家每月1号的气表读数．
（1）直接写出小明家1月份的用气量____________立方米及1－6月平均每月用气量为_______立方米．
（2）已知小明家2月份的气费为36元，试求他家6月份需交气费多少元？
（3）7月份放暑假后，小明的爷爷、奶奶及表哥来到家里和小明一起生活，并多次请客，用气量明显增加，比6月份多用气12立方米，试求小明家7月份需交纳气费多少元？
22．综合与探究
特例感知：（1）如图1，线段，C为线段AB上的一个动点，点D，E分别是AC，BC的中点．
①若，则线段DE的长为________cm．
②设，则线段DE的长为________cm．
知识迁移：（2）我们发现角的很多规律和线段一样，如图2，若，OC是内部的一条射线，射线OM平分，射线ON平分，求的度数．
拓展探究：（3）已知在内的位置如图3所示，，，且，，求的度数．（用含的代数式表示）
23．规定关于x的一元一次方程的解为，则称该方程是“差解方程”，例如：的解为，则方程就是“差解方程”，据上述规定解答下列问题：
【定义理解】
（1）判断：方程______差解方程；（填“是”或“不是”）
（2）若关于x的一元一次方程是“差解方程”，求m的值；
【知识应用】
（3）若关于x的一元一次方程是“差解方程”，求的值；
（4）已知关于x的一元一次方程和都是“差解方程”，求代数式的值．
参考答案
1．【答案】C
【分析】分别从每个选项入手进行判断即可．
【详解】解：A、从上面看不满足题意，不符合题意；
B、从正面看不满足题意，不符合题意；
C、符合题意；
D、从正面看不满足题意，不符合题意，
故此题答案为C．
2．【答案】B
【分析】利用数轴比较有理数大小等知识，先根据相反数的定义确定的在数轴上的位置，然后根据数轴比较大小即可．
【详解】解：由数轴可知，，且，
∴数，，在数轴上的位置如图所示：
∴．
故此题答案为B．
3．【答案】D
【分析】根据三角形面积公式列出方程即可．
【详解】解：根据题意直角三角形两直角边的边长分别为，面积为6，
则，
故此题答案为D．
4．【答案】C
【分析】由方向角的定义逐项进行判断即可．
【详解】解：由图中的各个方向角可知，
的方向是南偏西25°，因此选项A不符合题意；
的方向是北偏西，因此选项B 不符合题意；
的方向是北偏东，因此选项C符合题意；
OD的方向为南偏东45°，即东南方向，因此选项D不符合题意；
故此题答案为C．
5．【答案】D
【分析】利用等式的基本性质，将方程去分母得到结果，即可作出判断．
【详解】＝﹣1﹣
方程两边同乘以12，得：4(7x﹣5)＝﹣12﹣3(5x﹣1)，
故此题答案为D．
6．【答案】A
【详解】解：A选项：，故A选项正确；
B选项：，故B选项错误；
C选项：，，故C选项错误；
D选项：方程的解为，故D选项错误．
故此题答案为A．
7．【答案】224000
【分析】从展开图可得包装盒为长方体，先求出底面积，再乘以高计算即可．
【详解】解：包装盒的底面积为40×70=2800mm2，包装盒的高为80mm，
这种牛奶包装盒的体积是2800×80=224000．
8．【答案】
【分析】根据“地面气温是，高度每增加1千米，气温就下降”，即可列式计算．
【详解】解：由题意得7千米高空的气温是
9．【答案】a2b
【分析】根据同类项：所含字母相同，并且相同字母的指数也相同，可得出k的值，再合并同类项即可.
【详解】∵5akb与-4a2b是同类项，
∴k=2，
∴5akb+（-4a2b）=5a2b-4a2b=a2b.
10．【答案】
【分析】先根据“错误方程”的解求出a的值，从而可得原方程，再解一元一次方程即可．
【详解】解：由题意得：是方程的解
则，
解得，
因此，原方程为
解得
11．【答案】①②③
【分析】根据棱柱的特征、绝对值的意义、整式的定义、等式的性质，线段的特征判断即可．
【详解】解：①棱柱的上、下底面的形状和大小完全相同，故正确；
②数轴上的两个有理数，绝对值大的离原点远，故正确；
③，，都是整式，故正确；
④到线段两端点距离相等的点是线段垂直平分线上的点，故原说法错误；
⑤若，当时，则，故原说法错误．
12．【答案】或或
【分析】根据线段的四等分点有个，分三种情况并结合图形即可得出答案．
【详解】解：∵图中数轴的单位长度为，
∴，
①如图，当点靠近点时，
∵原点为的四等分点，
∴，
∴点代表的数为；

②如图，当点恰好是线段的中点时，
∵原点为的四等分点，
∴，
∴点代表的数为；

③如图，当点靠近点时，
∵原点为的四等分点，
∴，
∴点代表的数为；

综上所述，点代表的数为或或
13．【答案】(1)6
(2)
【分析】（1）先计算乘方和绝对值以及括号，再计算乘法，最后计算加减法即可．
（2）根据解一元一次方程的方法解答即可．
【详解】（1）解：
；
（2）解：
移项：，
合并：，
系数化1：，
移项：，即．
14．【答案】；10；；；；．
【分析】由，，求出，根据中点的定义，可知，再由，即可求解．
【详解】解：因为，（已知），
所以．
因为点是线段的中点（已知），
所以（线段中点的定义），
因为，
所以．
15．【答案】(1)等式的性质2；
(2)三；过程详见解析
【分析】（1）根据等式的性质解答即可；
（2）根据去分母、去括号、移项、合并同类项、未知数的系数化为1的步骤求解即可．
【详解】（1）两边都乘以4是根据等式的性质2，
故答案为：等式的性质2；
（2）第三步去掉分母后分子没加括号，故从第三步开始出现错误，
．
16．【答案】(1)王先生最后能回到出发点1楼；
(2)度
【分析】（1）把上下楼层的记录相加，根据有理数的加法运算法则进行计算，如果等于0则能回到1楼，否则不能；
（2）求出上下楼层所走过的总路程，然后乘以即可得解．
【详解】（1）解：
，
∴王先生最后能回到出发点1楼；
（2）解：王先生走过的路程是
，
他办事时电梯需要耗电（度．
答：他办事时电梯需要耗电度．
17．【答案】(1)见解析
(2)
【分析】（1）根据，，的范围，即可解答；
（2）根据，，的取值范围，判定、、的正负，根据绝对值的性质，即可解答．
【详解】（1）解：如图，
（2）解：、、，
，，，
．
18．【答案】(1)4
(2)，，
【分析】（1）将转化为再求解即可；
（2）画出图形，由，再在两段线段上分别加上相等的线段，所得线段也相等即可得出结论．
【详解】（1）解：，，
，
为线段的中点，
，
．
（2）如图，
为线段的中点，
，
，，
即，，
图中相等的线段有：，，．
19．【答案】(1)
(2)
(3)7
【分析】（1）根据合并同类项的法则计算；
（2）把整体代入计算；
（3）先去括号合并同类项，再整体代入计算．
【详解】（1）解：
（2）解：∵，
∴
；
（3）解：
，
∵，，，
∴，
∴，
∴，
即．
20．【答案】（1）57°，147°；（2）∠ACB＝180°－∠DCE，理由见解析；（3）∠DAB+∠CAE＝120°
【分析】（1）根据角的和差定义计算即可．
（2）利用角的和差定义计算即可．
（3）利用特殊三角板的性质，角的和差定义即可解决问题．
【详解】解：（1）由题意，
；
（2）∠ACB＝180°－∠DCE，
理由如下：
∵ ∠ACE＝90°－∠DCE，∠BCD＝90°－∠DCE，
∴ ∠ACB＝∠ACE＋∠DCE＋∠BCD
＝90°－∠DCE＋∠DCE＋90°－∠DCE
＝180°－∠DCE．
（3）结论：∠DAB+∠CAE=120°．
理由如下：
∵∠DAB+∠CAE=∠DAE+∠CAE+∠BAC+∠CAE=∠DAC+∠EAB，
又∵∠DAC=∠EAB=60°，
∴∠DAB+∠CAE=60°+60°=120°．
21．【答案】（1）；；（2）元；（3）元
【分析】（1）根据题意和表格中的数据，可以得出小明家月份的用气量和月份平均每月的用气量
（2）根据小明家月份的气费为元，可以计算出一级用气价格，再根据小明家月份的用气量超过立方米且不超过立方米，超过立方米的部分按第二级气量基数，结合题意，从而即可计算
（3）根据题意，可计算出小明家月的用气量，再结合题意，即可计算
【详解】（1）由表格数据可得：小明家月份的用气量为立方米；
月份平均每月的用气量为：立方米
故答案为：；
（2）小明家月份的气费为元，月份的气费量为：
一级用气价格为：（元/立方米）
月份的用气量为立方米，气量超过立方米且不超过立方米的部分按第二级气量基数，超出部分按一级用气价格的倍收取
月份小明家需交气费为：元
（3）小明家月份的用气量为：立方米，月份的用气量比月份的多立方米
月份的用气量为：立方米
气量超过立方米且不超过立方米的部分为第二级气量基数，超出部分按一级用气价格的倍收取，用气量超过立方米的部分为第三级气量基数，按一级用气价格的倍收取费用
月份小明家需交气费为：元
22．【答案】（1）①8，②8；（2）；（3）
【分析】（1）①利用求解即可；
②利用求解即可；
（2）利用角平分线的定义得到，，再利用角的和差关系进行计算即可；
（3）先求出，再利用角的和差关系进行转化即可．
【详解】解：（1）∵点D，E分别是AC，BC的中点，
∴，
∴．
（2）因为OM平分，ON平分，，
所以，．
所以．
（3）因为，，
所以．
因为，，
所以，，
所以，
所以．
23．【答案】（1）是；（2）；（3）16；（4）0
【分析】（1）根据差解方程的定义判断即可；
（2）根据差解方程的定义即可得出关于的一元一次方程，解之即可得出结论；
（3）根据差解方程的定义即可得出关于、的二元二次方程，整理即可得出；
（4）根据差解方程的概念列式得到关于、的两个方程，联立求解得到、的关系，得出，然后代入代数式进行计算即可求解．
【详解】解：（1）∵方程的解为，
∴方程是差解方程
（2）由题意可知，由一元一次方程可知，
∴，
解得；
（3）∵方程是“差解方程”，
∴，
解方程，得，
∴，
∴，即
（4）∵一元一次方程是“差解方程”，
∴，
解方程一元一次方程得
∴，整理得，
∵一元一次方程是“差解方程”，
∴，
解方程一元一次方程得，
∴，
∴，即，
∴原式．解： 第一步
第二步
第三步
第四步
第五步
1月
2月
3月
4月
5月
6月
7月
气表读数（立方米）
433
450
468
485
500
514
535