黑龙江省绥化市2024-2025学年七年级上学期12月月考 数学试题（含解析）

这是一份黑龙江省绥化市2024-2025学年七年级上学期12月月考 数学试题（含解析），共17页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
1．下列各数是无理数的是（ ）
A．0B．1C．D．
2．下列说法不正确的是（ ）
A．0.09的平方根是±0.3B．＝
C．1的立方根是±1D．0的立方根是0
3．下面四个图形中，与是对顶角的为（ ）
A．B．
C．D．
4．下列各数中，界于5和6之间的数是（ ）
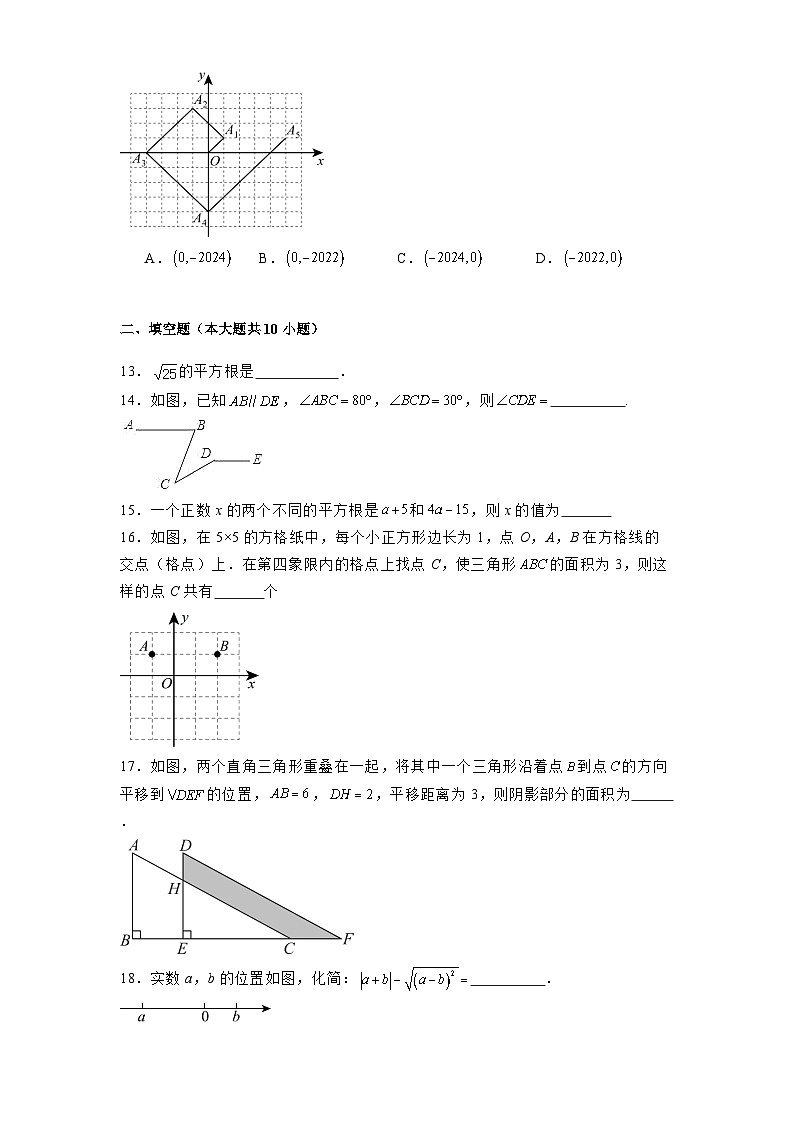
A．B．C．D．
5．如图，两条平行线，被直线所截，若，则的度数为（ ）

A．B．C．D．
6．在平面直角坐标系内，点p(x，x+3)的位置一定不在( )
A．第一象限B．第二象限C．第三象限D．第四象限
7．下列说法中①过一点有且只有一条直线与已知直线垂直；②直线外一点到这条直线的垂线段，叫做点到直线的距离；③开不尽方的数都是无理数；④过直线外一点有且只有一条直线与这条直线平行；⑤无限小数都是无理数，正确的个数是（ ）
A．1B．2C．3D．4
8．足球比赛中，每场比赛都要分出胜负每队胜1场得3分，负一场扣1分，某队在8场比赛中得到12分，若设该队胜的场数为x负的场数为y，则可列方程组为（ ）
A．B．
C．D．
9．在平面直角坐标系中，第二象限内的点P到x轴的距离是2，到y轴的距离是3，已知线段轴且，则点的坐标是（ ）
A．或B．或
C．或D．或
10．如图，将一副三角板按如图放置，则下列结论：①∠1=∠3，②如果∠2=30°时，则有ACDE，③如果∠2=30°，必有∠4=45°，④如果∠2=30°，则AB⊥DE．其中正确的有（ ）
A．①②③B．②③④C．①②④D．①②③④
11．如图，把长方形沿折叠后，点D，C分别落在，的位置．若，则是（ ）
A．B．C．D．
12．如图，在平面直角坐标系中，把一个点从原点开始，先向上平移1个单位，再向右平移1个单位，得到点；把先向上平移2个单位长度，再向左平移2个单位长度，得到点；把先向下平移3个单位长度，再向左平移3个单位长度，得到点：把先向下平移4个单位长度，再向右平移4个单位长度，得到点……按此方法进行下去，则点的坐标为（ ）
A．B．C．D．
二、填空题（本大题共10小题）
13．的平方根是 ．
14．如图，已知，，，则 .
15．一个正数x的两个不同的平方根是和，则x的值为
16．如图，在5×5的方格纸中，每个小正方形边长为1，点O，A，B在方格线的交点（格点）上．在第四象限内的格点上找点C，使三角形的面积为3，则这样的点C共有 个
17．如图，两个直角三角形重叠在一起，将其中一个三角形沿着点到点的方向平移到的位置，，，平移距离为3，则阴影部分的面积为 ．

18．实数a，b的位置如图，化简： ．
19．已知点到轴的距离为4，则点的坐标为 ．
20．已知、满足方程组，则的值为 ．
21．已知与的两边分别平行，且是的2倍少15°，那么、∠B的大小分别是 、 .
22．如图，在平面直角坐标系中，有若干个坐标分别为整数的点，其顺序按图中“”方向排列，如，，，，，，……．根据这个规律，第2024个点的坐标为 ．
三、解答题（本大题共7小题）
23．（1）计算：
（2）解方程组：
24．已知的算术平方根是2，的立方根是，c是的整数部分．
(1)求的值；
(2)求的平方根．
25．如图是由边长为的小正方形组成的网格，每个小正方形的顶点叫做格点，点均在格点上．若点的坐标分别为，请解答下列问题：
(1)直接写出点的坐标；
(2)将△ABC先向左平移2个单位长度，再向下平移1个单位长度得到，(点的对应点分别为，画出，并直接写出点的坐标；
(3)直接写出（2）中四边形的面积为 ．
26．如图，已知，平分，与相交于点，，试说明：，完成推理过程：
解：∵（已知），
∴_________，
∵平分（已知），
∴________（角平分线的定义）．
∵（已知），
∴______________（等量代换）．
∴（________________）．
27．如图，BD平分∠ABC，F在AB上，G在AC上，FC与BD相交于点H．∠GFH+∠BHC=180°，求证：．
28．某校准备组织七年级340名学生参加北京夏令营，已知用3辆小客车和1辆大客车每次可运送学生105人；用1辆小客车和2辆大客车每次可运送学生110人；
(1)每辆小客车和每辆大客车各能坐多少名学生？
(2)若学校计划租用小客车x辆，大客车y辆，一次送完，且恰好每辆车都坐满；
①请你设计出所有的租车方案；
②若小客车每辆需租金4000元，大客车每辆需租金8000元，请选出最省钱的租车方案，并求出最少租金．
29．在平面直角坐标系中，已知点，，，且满足，线段交轴于点，点是轴正半轴上的一点．

(1)求出点，的坐标；
(2)如图2，若，，且，分别平分，，求的度数；（用含的代数式表示）．
(3)如图3，坐标轴上是否存在一点，使得的面积和的面积相等？若存在，求出点坐标；若不存在，请说明理由．
参考答案
1．【答案】D
【分析】无理数包括三方面的数：①开方开不尽的根式，②含有的，③一些有规律的数，如0.010010001……等．无限不循环小数叫做无理数，根据无理数的定义逐个判断即可．
【详解】解：0，1和都是有理数，不是无理数，
是无理数，
故此题答案为D．
2．【答案】C
【分析】根据平方根，算术平方根和立方根的定义分别判断即可．
【详解】解：A、0.09的平方根是±0.3，故选项不符合题意；
B、＝，故选项不符合题意；
C、1的立方根是，错误，故选项符合题意；
D、0的立方根是0，故选项不符合题意；
故此题答案为C．
3．【答案】C
【分析】两条边互为反向延长线的两个角叫对顶角，根据定义结合图形逐个判断即可．
【详解】解：A、不符合对顶角的定义，故本选项不符合题意；
B、不符合对顶角的定义，故本选项不符合题意；
C、符合对顶角的定义，故本选项符合题意；
D、不符合对顶角的定义，故本选项不符合题意；
故此题答案为C．
4．【答案】D
【分析】找出在与之间、与之间的无理数即可求解．
【详解】∵，∴56．
故此题答案为D．
5．【答案】B
【分析】先求解，再利用平行线的性质可得答案．
【详解】解：∵，
∴，
∵，
∴，
故此题答案为B
6．【答案】D
【分析】根据题意先判断出P的横纵坐标的符号，进而判断出相应象限即可．
【详解】解：当x为0或正数的时候，x+3一定为正数，所以点P可能在第一象限，一定不在第四象限，
当x为负数的时候，x+3可能为正数，也可能为负数，所以点P可能在第二象限，也可能在第三象限，
综上可知点p(x，x+3)的位置一定不在第四象限.
故此题答案为D．
7．【答案】B
【分析】根据直线的性质，点到直线的距离的定义，线段的性质，实数的定义对各小题分析判断即可得解．
【详解】解：①过平面上的一点有且只有一条直线与已知直线垂直，原说法错误；
②直线外一点到这条直线的垂线段的长度，叫做点到直线的距离，原说法错误；
③开不尽方的数都是无理数，这个说法正确；
④过直线外一点有且只有一条直线与这条直线平行，故这个说法正确；
⑤无限不循环小数都是无理数，原说法错误；
综上所述：正确的有③④共2个．
故此题答案为B．
8．【答案】A
【分析】设这个队胜x场，负y场，根据在8场比赛中得到12分，列方程组即可．
【详解】解：设这个队胜x场，负y场，
根据题意，得 ．
故此题答案为A．
9．【答案】A
【分析】根据第二象限内点的特点及点到坐标轴的距离定义，即可判断出点P的坐标．然后根据已知条件得到点Q的坐标．
【详解】点P到x轴的距离是2，则点P的纵坐标为±2，
点P到y轴的距离是3，则点P的纵坐标为±3，
由于点P在第二象限，故P坐标为（−3，2）．
∵线段PQ∥y轴且PQ＝5，
∴点Q的坐标是（−3，7）或（−3，−3）
故此题答案为A．
10．【答案】D
【分析】先根据同角的余角相等判断①；根据平行线的判定定理判断②；然后根据平行线的判定定理及性质定理判断③；最后根据平行线的性质及垂直的定义判断④．
【详解】解：∵∠1+∠2=90°，∠3+∠2=90°，
∴∠1=∠3，故①正确；
∵∠2=30°，
∴∠1=60°，
又∵∠E=60°，
∴∠1=∠E，
∴AC∥DE，故②正确；
∵∠2=30°，
根据②得到AC∥DE，
∴∠4=∠C=45°，故③正确；
∵∠2=30°，
由③知∠4=∠C=45°，
∵∠B=45°，
∴∠B+∠4=90°，
∴AB⊥DE，故④正确；
综上，四个选项均正确，
故此题答案为D．
11．【答案】B
【分析】由折叠的性质可知，，，由，可得，根据，计算求解即可．
【详解】解：由折叠的性质可知，，，
∵，
∴，
∴，
故此题答案为B．
12．【答案】A
【分析】先根据平移规律得到第n次变换时，相当于把点的坐标向右或向左平移n个单位长度，再向右或向上平移n个单位长度得到下一个点，然后推出每四次坐标变换为一个循环，得到点的坐标为，由此求解即可．
【详解】解：∵把一个点从原点开始向上平移1个单位，再向右平移1个单位，得到点；
把点向上平移2个单位，再向左平移2个单位，得到点；
把点向下平移3个单位，再向左平移3个单位，得到点；
把点向下平移4个单位，再向右平移4个单位，得到点，
∴第n次变换时，相当于把点的坐标向右或向左平移n个单位长度，再向下或向上平移n个单位长度得到下一个点，
∵O到是向右平移1个单位长度，向上平移1个单位长度，到是向左2个单位长度，向上平移2个单位长度，到是向左平移3个单位长度，向下平移3个单位长度，到是向右平移4个单位长度，向下平移4个单位长度，到是向右平移5个单位长度，向上平移5个单位长度，
∴可以看作每四次坐标变换为一个循环，
∴点的坐标为，
∵，
∴点的坐标为，
故此题答案为A．
13．【答案】±
【分析】根据平方运算，可得平方根、算术平方根．
【详解】的平方根是±．
14．【答案】
【分析】根据两直线平行，内错角相等以及三角形外角的性质解答即可．
【详解】反向延长DE交BC于M．
∵AB∥DE，∴∠BMD=∠ABC=80°，∴∠CMD=180°﹣∠BMD=100°；
又∵∠CDE=∠CMD+∠BCD，∴∠CDE=100°+30°=130°．
15．【答案】49
【分析】根据一个数的两个平方根互为相反数即可求出a的值，从而可求出x的值．
【详解】解：∵实数的两个不同的平方根为和，
∴，
解得：，
∴．
16．【答案】3
【分析】求得的长，根据三角形的面积公式即可确定点 C所在直线，从而确定点C的位置．
【详解】解：由，使三角形的面积为3，
则边上的高为2，
即此点到所在直线的距离是2，
位置要在第四象限，且在格点上，这样的点可以是，，，共有3个．
17．【答案】15
【分析】先判断出阴影部分面积等于梯形的面积，再根据平移变化只改变图形的位置不改变图形的形状可得，然后求出，根据平移的距离求出，然后利用梯形的面积公式列式计算即可得解．
【详解】解：将三角形沿着点到点的方向平移到的位置，
，
阴影部分的面积等于梯形的面积，
由平移得，，
，，
，
阴影部分的面积为
18．【答案】
【分析】先根据数轴推出，再化简绝对值和计算算术平方根后合并同类项即可得到答案．
【详解】解：由数轴可知，
∴，
∴
19．【答案】或
【分析】根据点P到x轴的距离，可确定纵坐标为4或，从而可得答案．
【详解】∵点到x轴的距离为4，
∴或，
∴点P的坐标为或
20．【答案】1
【分析】将两式相减即可得到的值．
【详解】解：，
①②得：
21．【答案】 、， 、.
【分析】分两种情形分别构建方程组即可解决问题．
【详解】∵∠α与∠β的两边分别平行，∴α=β或α+β=180°，∴或，解得：或．
22．【答案】
【分析】根据图形推导出当n为奇数时，第n个正方形每条边上有个点，连同前边所有正方形共有个点，且终点为；当n为偶数时，第n个正方形每条边上有个点，连同前边所以正方形共有点，且终点为．而，由，解得．由规律可知，第44个正方形每条边上有个点，且终点坐标为，由图可知，再倒着推1个点的坐标即可得到答案．
【详解】解：由图可知：第一个正方形每条边上有2个点，共有个点，且终点为；
第二个正方形每条边上有3个点，连同第一个正方形共有个点，且终点为；
第三个正方形每条边上有4个点，连同前两个正方形共有个点，且终点为；
第四个正方形每条边上有5个点，连同前两个正方形共有个点，且终点为；
故当n为奇数时，第n个正方形每条边上有个点，连同前边所有正方形共有个点，且终点为；当n为偶数时，第n个正方形每条边上有个点，连同前边所以正方形共有点，且终点为．
而，
，
解得：．
由规律可知，第44个正方形每条边上有个点，且终点坐标为，由图可知，再倒着推1个点的坐标为：．
23．【答案】（1）；（2）．
【分析】（1）利用绝对值，立方根，实数的运算法则计算，然后根据运算顺序解答即可；
（2）利用加减消元法解方程即可得解．
【详解】（1）解：
；
（2）解：，
得，即，
∴③，
得，
得：，
∴方程组的解是．
24．【答案】(1)，，
(2)
【分析】（1）先估算的大小，求出它的整数部分c，再根据的算术平方根是2，的立方根是，列出关于a，b的方程，解方程求出a，b即可；
（2）把（1）中所求的a，b，c代入进行计算，从而求出它的平方根即可．
【详解】（1）解：∵，即，
∴的整数部分4，即，
∵的算术平方根是2，的立方根是，
∴，，
解得：，，；
（2）解：由（1）可知：，，，
∴
=6，
∴的平方根为．
25．【答案】(1)
(2)见解析，
(3)
【分析】（1）根据两点坐标，画出平面直角坐标系即可；
（2）利用平移变换的性质分别作出的对应点即可；
（3）把四边形面积看成矩形面积减去周围特殊特性的面积即可．
【详解】（1）解：平面直角坐标系如图所示：
（2）解：如图，即为所求，
（3）解：四边形的面积
26．【答案】；；；内错角相等，两直线平行
【分析】根据平行线的性质和判定解答即可．
【详解】解：∵（已知），
∴（两直线平行，同位角相等）．
∵平分（已知），
∴（角平分线的定义）．
∵（已知），
∴（等量代换）．
∴（内错角相等，两直线平行）．
27．【答案】见解析．
【分析】求出∠GFH＋∠FHD＝180°，根据平行线的判定得出FG∥BD，根据平行线的性质得出∠1＝∠ABD，求出∠2＝∠ABD即可．
【详解】∵∠GFH+∠BHC=180°，∠BHC=∠FHD
∴∠GFH+∠FHD =180°
∴FG//BD
∴∠1=∠ABD
∵BD平分∠ABC
∴∠2=∠ABD
∴∠1=∠2．
28．【答案】(1)每辆小客车和每辆大客车各能坐20名学生，45名学生
(2)①一共有2种租车方案：方案一，租用小客车17辆，大客车0辆；方案二：租用小客车8辆，大客车4辆；②最省钱的方案是8辆小客车，4辆大客车，租金为64000元
【分析】（1）设小客车能坐a名学生，大客车能坐b名学生，根据用3辆小客车和1辆大客车每次可运送学生105人；用1辆小客车和2辆大客车每次可运送学生110人列出方程组求解即可；
（2）①根据（1）所求可得方程，求出方程的非负整数解即可得到答案；②求出两种方案的花费即可得到答案．
【详解】（1）解：设小客车能坐a名学生，大客车能坐b名学生，
由题意得，
解得，
答：每辆小客车和每辆大客车各能坐20名学生，45名学生；
（2）解：①由题意得，，
∴，
∵x，y都是整数，
∴一定是整数，
∴一定是4的倍数，
∴或，
∴一共有2种租车方案：方案一，租用小客车17辆，大客车0辆；方案二：租用小客车8辆，大客车4辆；
②解：方案一的费用为元，
方案二的费用为元，
∵，
∴最省钱的方案是8辆小客车，4辆大客车，租金为64000元．
29．【答案】(1)，
(2)
(3)存在满足条件的点，其坐标为或或或
【分析】（1）根据非负数的性质得，，解方程即可得出和的值，从而得出答案；
（2）过点作，交轴于点，根据角平分线的定义得，，再利用平行线的性质可得答案；
（3）连接，利用两种方法表示的面积，可得点的坐标，再分点在轴或轴上两种情形，分别表示的面积，从而解决问题．
【详解】（1）解：，
，，
，，
，；
（2）解：过点作，交轴于点，如图所示：

，
，
，
，
，，
，
，分别平分，，，
，，
，，
；
（3）解：存在．
理由如下：连接，如图所示：

设，
，
，解得，
点坐标为，
，，，
∴，
当点在轴上时，设，
，
，解得或，
此时点坐标为或；
当点在轴上时，设，则，解得或，
此时点坐标为或，
综上可知存在满足条件的点，其坐标为或或或．