2024-2025学年度绵阳市北川县九年级期末数学质量监测试卷

这是一份2024-2025学年度绵阳市北川县九年级期末数学质量监测试卷，共8页。
一．选择题（共12小题，36分）
1．下列图案中是中心对称图形但不是轴对称图形的是（ ）
A．B．C．D．
2．用配方法解一元二次方程x2﹣6x﹣2＝0，配方后得到的方程是（ ）
A．（x﹣3）2＝2B．（x﹣3）2＝8C．（x﹣3）2＝11D．（x+3）2＝9
3．如图，有一圆弧形桥拱，拱形的半径OA＝10m，桥拱的跨度AB＝16m，则拱高CD为（ ）
A．4mB．6mC．8mD．10m
4．如图，正六边形ABCDEF内接于⊙O，若⊙O的周长是6π，则正六边形的边长是（ ）
A．B．3C．6D．
5．如图，电路图上有4个开关A，B，C，D和1个小灯泡，同时闭合开关A，B或同时闭合开关C，D都可以使小灯泡发光．同时闭合两个开关小灯泡发光的概率是（ ）
A．B．C．D．
6．如图，蒙古包可近似地看作由圆锥和圆柱组成，若用毛毡搭建一个底面圆面积为36πm2，圆柱高为4m，圆锥高为2m的蒙古包，则需要毛毡的面积是（ ）
A．B．144πm2
C．D．216πm2
7．已知点A是反比例函数的图象上的一个动点，连接OA，若将线段OA绕点O顺时针旋转90°得到线段OB，则点B所在图象的函数表达式是（ ）
A．y＝3x（x＞0）B．y＝﹣6x（x＜0）
C．D．
8．如图，将△ABC绕点C逆时针旋转，得到△CDE，若点A的对应点D恰好在线段AB上，且CD平分∠ACB，记线段BC与DE的交点为F．下列结论中，不正确的是（ ）
A．CA＝CDB．△CDE≌△CDAC．∠BDF＝∠ACDD．DF＝EF
9．某幢建筑物，从10米高的窗口A用水管和向外喷水，喷的水流呈抛物线（抛物线所在平面与墙面垂直），（如图）如果抛物线的最高点M离墙1米，离地面米，则水流下落点B离墙距离OB是（ ）
A．2米B．3米C．4米D．5米
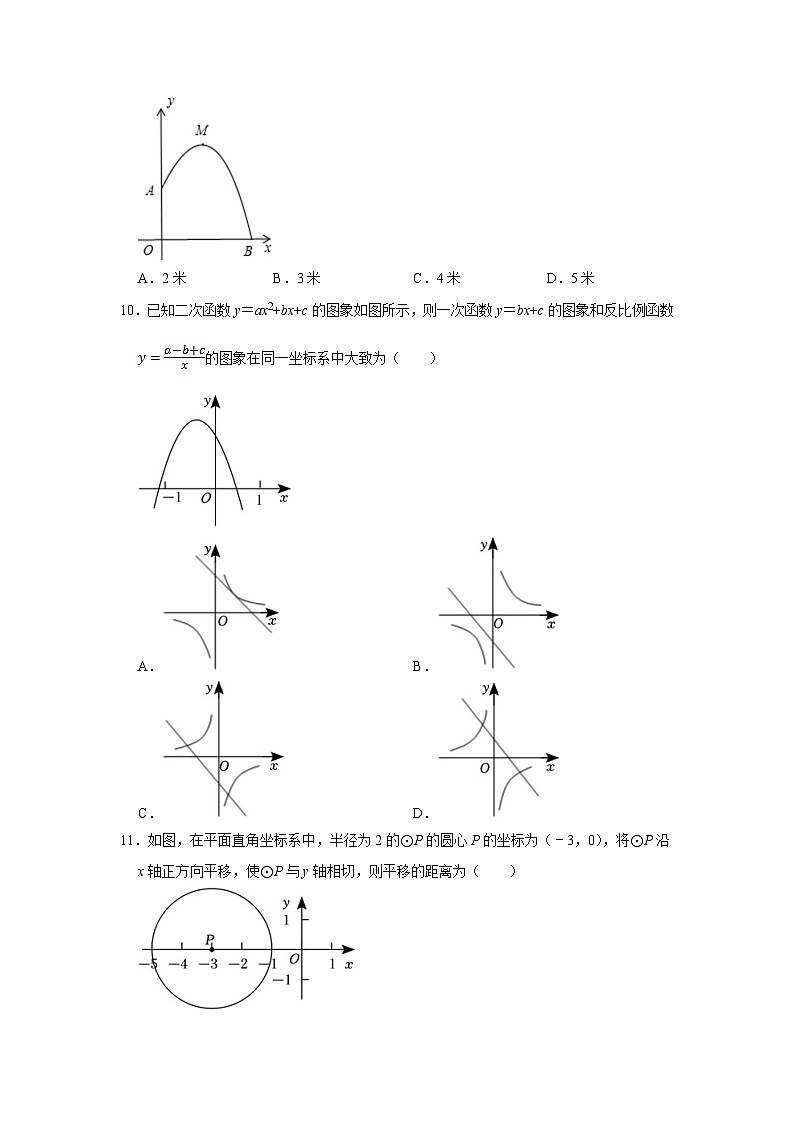
10．已知二次函数y＝ax2+bx+c的图象如图所示，则一次函数y＝bx+c的图象和反比例函数的图象在同一坐标系中大致为（ ）
A．B．
C．D．
11．如图，在平面直角坐标系中，半径为2的⊙P的圆心P的坐标为（﹣3，0），将⊙P沿x轴正方向平移，使⊙P与y轴相切，则平移的距离为（ ）
A．1或5B．1或3C．3或5D．1
12．二次函数y＝ax2+b的图象如图所示，则一次函数y＝ax+b的图象可能是（ ）
A．B．C．D．
二．填空题（共6小题,共24分）
13．如果一元二次方程x2+3x﹣2＝0的两个根为x1，x2，则x13+3x12﹣x1x2+2x2＝ ．
14．如图，四边形ABCD内接于⊙O，点E在CD的延长线上，若∠ADE＝80°，则∠AOC的度数是 ．
15．小红帮助母亲预算家庭4月份电费开支情况，下表是小红家4月初连续8天每天早上电表显示的读数：
若每度电收费0.42元，估计小红家4月份（按30天计）的电费是 元．（注：电表计数器上先后显示读数之差就是这段时间内消耗电能的度数）
16．用一根长60cm的铁丝围成一个矩形，则矩形的最大面积为 cm2．
17．如图，平面直角坐标系中，△OAB和△BCD都是等腰直角三角形，且∠A＝∠C＝90°，点B、D都在x轴上，点A、C都在反比例函数y（x＞0）的图象上，则点C的横坐标为 ．
18．如图，在△ABC中，∠CAB＝60°，AB＝10，AC＝6，将线段BC绕着点B逆时针旋转60°得到BC′，连接AC′，CC′，则△ABC′的面积为 ．
三．解答题（共90分）
19．（8分）解方程：2（x﹣1）2＝x﹣1．
20．（10分）如图，在平面直角坐标系中，△ABC的三个顶点分别为A（﹣4，3），B（﹣1，2），C（﹣2，1）．
（1）画出△ABC关于原点O对称的△A1B1C1，并写出点B1的坐标；
（2）画出△ABC绕原点O顺时针方向旋转90°得到的△A2B2C2，并写出点A2的坐标；
（3）在（2）的旋转过程中，求点B旋转到点B2所经过的路线长（结果保留π）．
21．（10分）已知关于x的一元二次方程x2﹣（2k+4）x+k2+4k+3＝0．
（1）求证：不论k取何值，此一元二次方程总有两个不相等的实数根；
（2）若此一元二次方程的两根是Rt△ABC两直角边AB、AC的长，斜边BC的长为10，求k的值．
22．（10分）中山市图书馆购进一批图书供学生阅读，为了合理配备各类图书，从全市学生中随机抽取了部分学生进行了问卷调查．问卷设置了五种选项：A“艺术类”，B“文学类”，C“科普类”，D“体育类”，E“其他类”，每名学生必须且只能选择其中最喜爱的一类图书，将调查结果整理绘制成如下两幅不完整的统计图．根据以上信息，解答下列问题：
（1）此次被调查的学生人数为 名，并补全条形统计图；
（2）在扇形统计图中，A“艺术类”所对应的圆心角度数是 度；
（3）李老师准备从甲、乙、丙、丁四位学生中随机选择两位进行访问．请用列表或画树状图的方法，求李老师选中乙、丙这两位同学的概率．
23．（12分）如图，在矩形ABCD中，AB＝4，BC＝3．O为AC的中点，动点P从点A出发，沿折线A→B→C运动，当它到达点C时停止运动，设点P运动的路程为x（x＞0），连接OP，设△AOP的面积为y1．
（1）直接写出y1与x的函数关系式为： ．
（2）在给出的平面直角坐标系中画出y1的函数图象，并写出这个函数的一条性质： ；
（3）如图2，的图象如图所示，根据函数图象，直接写出当y1≤y2时x的取值范围是 .（结果保留一位小数，误差不超过0.2）
24．（12分）直角三角形的两条直角边的长相差2cm，面积是24cm2，求两条直角边的长．
25．（14分）如图，在△ABC中，AB＝AC，以AB为直径的⊙O分别与BC，AC交于点D，E，过点D作DF⊥AC于点F．
（1）判断DF与是⊙O的位置关系，并证明你的结论．
（2）若⊙O的半径为4，∠CDF＝22.5°，求阴影部分的面积．
26．（14分）如图在平面直角坐标系中已知抛物线yx2x﹣2交x轴于点A、B，交y轴于点C．
（1）求线段BC的长；
（2）点P为第三象限内抛物线上一点，连接BP，过点C作CE∥BP交x轴于点E，连接PE，求△BPE面积的最大值及此时点P的坐标；
（3）在（2）的条件下，以y轴为对称轴，将抛物线yx2x﹣2对称，对称后点P的对应点为点P′，点M为对称后的抛物线对称轴上一点，N为平面内一点，是否存在以点A、P′、M、N为顶点的四边形是菱形，若存在，直接写出点N的坐标，若不存在，则请说明理由．
日期
1
2
3
4
5
6
7
8
电表显示度数
21
24
28
33
39
42
46
49