2025高考数学一轮复习-第7章-立体几何与空间向量-第4讲 空间直线、平面的平行系【课件】

这是一份2025高考数学一轮复习-第7章-立体几何与空间向量-第4讲 空间直线、平面的平行系【课件】，共44页。PPT课件主要包含了教材再现四基诊断，一条直线，相交直线，l⊄α，重点串讲能力提升，平行关系的综合应用等内容，欢迎下载使用。
课程标准　1.以立体几何的定义、公理和定理为出发点，认识和理解空间中线面平行、面面平行的有关性质与判定定理．　2.能运用公理、定理和已获得的结论证明一些有关空间图形的平行关系的简单命题．
1．直线与平面平行(1)直线与平面平行的定义直线l与平面α没有公共点，则称直线l与平面α平行．
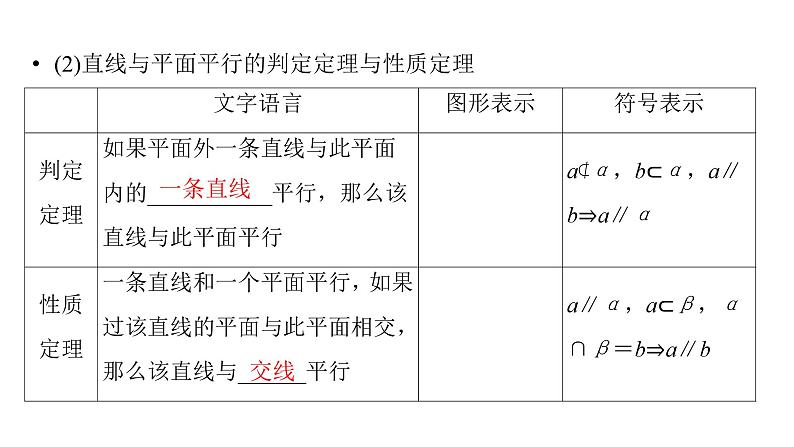
(2)直线与平面平行的判定定理与性质定理
2.平面与平面平行(1)平面与平面平行的定义没有公共点的两个平面叫做平行平面．
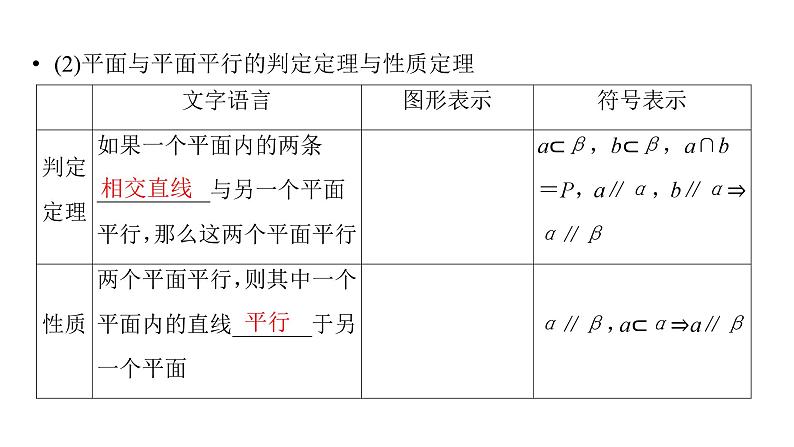
(2)平面与平面平行的判定定理与性质定理
1.平行关系中的三个重要结论(1)垂直于同一条直线的两个平面平行，即若a⊥α，a⊥β，则α∥β.(2)平行于同一平面的两个平面平行，即若α∥β，β∥γ，则α∥γ.(3)垂直于同一个平面的两条直线平行，即若a⊥α，b⊥α，则a∥b.
2．三种平行关系的转化
1．判断下列结论是否正确(正确的在括号内打“√”，错误的在括号内打“×”).(1)若一条直线和平面内一条直线平行，那么这条直线和这个平面平行．(　　)(2)若直线a∥平面α，P∈α，则过点P且平行于直线a的直线有无数条．(　　)(3)如果一个平面内的两条直线平行于另一个平面，那么这两个平面平行．(　　)
(4)如果两个平面平行，那么分别在这两个平面内的两条直线平行或异面．(　　)解析：(1)若一条直线和平面内的一条直线平行，那么这条直线和这个平面平行或在平面内，故(1)错误．(2)若a∥α，P∈α，则过点P且平行于a的直线只有一条，故(2)错误．(3)如果一个平面内的两条直线平行于另一个平面，则这两个平面平行或相交，故(3)错误．
2．如果直线a∥平面α，那么直线a与平面α内的(　　)A．一条直线不相交B．两条直线不相交C．无数条直线不相交D．任意一条直线都不相交解析：因为直线a∥平面α，直线a与平面α无公共点，因此直线a与平面α内的任意一条直线都不相交．
解析：①由线面平行的判定定理知l⊄α；②由线面平行的判定定理知l⊄α.
直线与平面平行的判定与性质
角度1　直线与平面平行的判定例1　如图，在四棱锥P­ABCD中，底面ABCD是平行四边形，E，F分别是BC，PD的中点，求证：(1)PB∥平面ACF；(2)EF∥平面PAB.
[证明]　(1)如图，连接BD交AC于O，连接OF.∵四边形ABCD是平行四边形，∴O是BD的中点．又∵F是PD的中点，∴OF∥PB.又∵OF⊂平面ACF，PB⊄平面ACF，∴PB∥平面ACF.
判断或证明线面平行的常用方法(1)利用线面平行的定义(无公共点).(2)利用线面平行的判定定理(a⊄α，b⊂α，a∥b⇒a∥α).(3)利用面面平行的性质(α∥β，a⊂α⇒a∥β).(4)利用面面平行的性质(α∥β，a⊄β，a∥α⇒a∥β).
如图，四边形ABCD为矩形，ED⊥平面ABCD，AF∥ED.求证：BF∥平面CDE.
证明：法一：∵四边形ABCD为矩形，∴AB∥CD.∵AB⊄平面CDE，CD⊂平面CDE，∴AB∥平面CDE.又AF∥ED，∵AF⊄平面CDE，ED⊂平面CDE，∴AF∥平面CDE.∵AF∩AB＝A，AB⊂平面ABF，AF⊂平面ABF，∴平面ABF∥平面CDE，又BF⊂平面ABF，∴BF∥平面CDE.
法二：如图，在ED上取点N，使DN＝AF，连接NC，NF，∵AF∥DN，且AF＝DN，∴四边形ADNF为平行四边形，∴AD∥FN，且AD＝FN.又四边形ABCD为矩形，AD∥BC且AD＝BC，∴FN∥BC，且FN＝BC，∴四边形BCNF为平行四边形，∴BF∥NC.∵BF⊄平面CDE，NC⊂平面CDE，∴BF∥平面CDE.
角度2　直线与平面平行的性质定理的应用例2　如图所示，在四棱锥P­ABCD中，四边形ABCD是平行四边形，M是PC的中点，在DM上取一点G，过G和PA作平面交BD于点H.求证：PA∥GH.
[证明]　如图所示，连接AC交BD于点O，连接OM，∵四边形ABCD是平行四边形，∴O是AC的中点．又M是PC的中点，∴PA∥OM.又OM⊂平面BMD，PA⊄平面BMD，∴PA∥平面BMD.又平面PAHG∩平面BMD＝GH，∴PA∥GH.
应用线面平行的性质定理的关键是确定交线的位置，有时需要经过已知直线作辅助平面确定交线．
如图所示，已知四边形ABCD是正方形，四边形ACEF是矩形，M是线段EF的中点．(1)求证：AM∥平面BDE；(2)若平面ADM∩平面BDE＝l，平面ABM∩平面BDE＝m，试分析l与m的位置关系，并证明你的结论．
(1)证明：如图，记AC与BD的交点为O，连接OE.因为O，M分别为AC，EF的中点，且四边形ACEF是矩形，所以EM∥OA且EM＝OA，所以四边形AOEM是平行四边形，所以AM∥OE.又因为OE⊂平面BDE，AM⊄平面BDE，所以AM∥平面BDE.
(2)解：l∥m，证明如下：由(1)知AM∥平面BDE.又AM⊂平面ADM，平面ADM∩平面BDE＝l，所以l∥AM.同理，AM∥平面BDE.又AM⊂平面ABM，平面ABM∩平面BDE＝m，所以m∥AM，所以l∥m.
平面与平面平行的判定与性质
例3　如图所示，在三棱柱ABC­A1B1C1中，过BC的平面与上底面A1B1C1交于GH(GH与B1C1不重合).(1)求证：BC∥HG；(2)若E，F，G分别是AB，AC，A1B1的中点，求证：平面EFA1∥平面BCHG.
[证明]　(1)∵在三棱柱ABC­A1B1C1中，平面ABC∥平面A1B1C1，又平面BCHG∩平面ABC＝BC，且平面BCHG∩平面A1B1C1＝HG，∴由面面平行的性质定理得BC∥HG.
(2)∵E，F分别为AB，AC的中点，∴EF∥BC.∵EF⊄平面BCHG，BC⊂平面BCHG，∴EF∥平面BCHG.又G，E分别为A1B1，AB的中点，A1B1綉AB，∴A1G綉EB，∴四边形A1EBG是平行四边形，∴A1E∥GB.∵A1E⊄平面BCHG，GB⊂平面BCHG，∴A1E∥平面BCHG.又∵A1E∩EF＝E，A1E，EF⊂平面EFA1，∴平面EFA1∥平面BCHG.
证明面面平行的常用方法(1)利用面面平行的判定定理．(2)利用垂直于同一条直线的两个平面平行(l⊥α，l⊥β⇒α∥β).(3)利用面面平行的传递性，即两个平面同时平行于第三个平面，则这两个平面平行(α∥β，β∥γ⇒α∥γ).
如图，四棱柱ABCD­A1B1C1D1的底面ABCD是正方形．(1)证明：平面A1BD∥平面CD1B1；(2)若平面ABCD∩平面B1D1C＝l，证明：B1D1∥l.
证明：(1)由题设知BB1綉DD1，所以四边形BB1D1D是平行四边形，所以BD∥B1D1.又BD⊄平面CD1B1，B1D1⊂平面CD1B1，所以BD∥平面CD1B1.因为A1D1綉B1C1綉BC，所以四边形A1BCD1是平行四边形，所以A1B∥D1C.又A1B⊄平面CD1B1，D1C⊂平面CD1B1，所以A1B∥平面CD1B1.又BD∩A1B＝B，BD，A1B⊂平面A1BD，所以平面A1BD∥平面CD1B1.
(2)由(1)知平面A1BD∥平面CD1B1，又平面ABCD∩平面B1D1C＝l，平面ABCD∩平面A1BD＝BD，所以直线l∥BD.在四棱柱ABCD­A1B1C1D1中，四边形BDD1B1为平行四边形，所以B1D1∥BD，所以B1D1∥l.
所以PR∥平面A1D1DA.又PQ∥平面A1D1DA，PQ∩PR＝P，PQ，PR⊂平面PQR，所以平面PQR∥平面A1D1DA.
证明平行关系的常用方法熟练掌握线线、线面、面面平行关系间的相互转化是解决线线、线面、面面平行的综合问题的关键；面面平行判定定理的推论也是证明面面平行的一种常用方法．
如图所示，四边形EFGH为空间四边形ABCD的一个截面，若截面为平行四边形．(1)求证：AB∥平面EFGH，CD∥平面EFGH；(2)若AB＝4，CD＝6，求四边形EFGH周长的取值范围．
(1)证明：∵四边形EFGH为平行四边形，∴EF∥HG.∵HG⊂平面ABD，EF⊄平面ABD，∴EF∥平面ABD.又∵EF⊂平面ABC，平面ABD∩平面ABC＝AB，∴EF∥AB.又∵AB⊄平面EFGH，EF⊂平面EFGH，∴AB∥平面EFGH.同理可证，CD∥平面EFGH.