2024年山东省东营市中考数学模拟试题（word版，含答案）

这是一份2024年山东省东营市中考数学模拟试题（word版，含答案），共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（3分）﹣2019的相反数是（ ）
A．﹣2019B．2019C．﹣D．
2．（3分）下列运算正确的是（ ）
A．3x3﹣5x3＝﹣2xB．8x3÷4x＝2x
C．＝D．+＝
3．（3分）将一副三角板（∠A＝30°，∠E＝45°）按如图所示方式摆放，使得BA∥EF，则∠AOF等于（ ）
A．75°B．90°C．105°D．115°
4．（3分）下列图形中，是轴对称图形的是（ ）
A．B．
C．D．
5．（3分）篮球联赛中，每场比赛都要分出胜负，每队胜1场得2分，负1场得1分，某队在10场比赛中得到16分．若设该队胜的场数为x，负的场数为y，则可列方程组为（ ）
A．B．
C．D．
6．（3分）从1，2，3，4中任取两个不同的数，分别记为a和b，则a2+b2＞19的概率是（ ）
A．B．C．D．
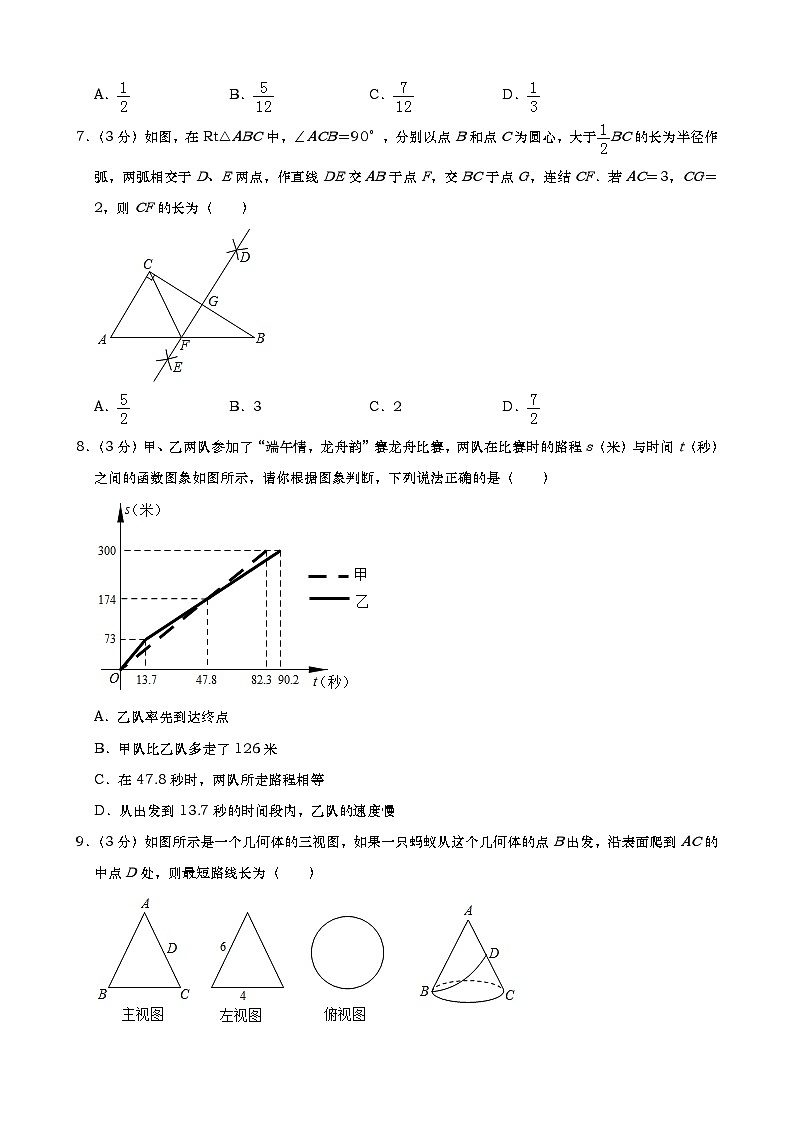
7．（3分）如图，在Rt△ABC中，∠ACB＝90°，分别以点B和点C为圆心，大于BC的长为半径作弧，两弧相交于D、E两点，作直线DE交AB于点F，交BC于点G，连结CF．若AC＝3，CG＝2，则CF的长为（ ）
A．B．3C．2D．
8．（3分）甲、乙两队参加了“端午情，龙舟韵”赛龙舟比赛，两队在比赛时的路程s（米）与时间t（秒）之间的函数图象如图所示，请你根据图象判断，下列说法正确的是（ ）
A．乙队率先到达终点
B．甲队比乙队多走了126米
C．在47.8秒时，两队所走路程相等
D．从出发到13.7秒的时间段内，乙队的速度慢
9．（3分）如图所示是一个几何体的三视图，如果一只蚂蚁从这个几何体的点B出发，沿表面爬到AC的中点D处，则最短路线长为（ ）
A．3B．C．3D．3
10．（3分）如图，在正方形ABCD中，点O是对角线AC、BD的交点，过点O作射线OM、ON分别交BC、CD于点E、F，且∠EOF＝90°，OC、EF交于点G．给出下列结论：①△COE≌△DOF；②△OGE∽△FGC；③四边形CEOF的面积为正方形ABCD面积的；④DF2+BE2＝OG•OC．其中正确的是（ ）
A．①②③④B．①②③C．①②④D．③④
二、填空题：本大题共8小题，其中11-14题每小题3分，15-18题每小题3分，共28分．只要求填写最后结果．
11．（3分）2024年1月12日，“五指山”舰正式入列服役，是我国第六艘071型综合登陆舰艇，满载排水量超过20000吨，20000用科学记数法表示为 ．
12．（3分）因式分解：x（x﹣3）﹣x+3＝ ．
13．（3分）东营市某中学为积极响应“书香东营，全民阅读”活动，助力学生良好阅读习惯的养成，形成浓厚的阅读氛围，随机调查了部分学生平均每天的阅读时间，统计结果如表所示，则在本次调查中，学生阅读时间的中位数是 ．
14．（3分）已知等腰三角形的底角是30°，腰长为2，则它的周长是 ．
15．（4分）不等式组的解集为 ．
16．（4分）如图，AC是⊙O的弦，AC＝5，点B是⊙O上的一个动点，且∠ABC＝45°，若点M、N分别是AC、BC的中点，则MN的最大值是 ．
17．（4分）如图，在平面直角坐标系中，△ACE是以菱形ABCD的对角线AC为边的等边三角形，AC＝2，点C与点E关于x轴对称，则点D的坐标是 ．
18．（4分）如图，在平面直角坐标系中，函数y＝x和y＝﹣x的图象分别为直线l1，l2，过l1上的点A1（1，）作x轴的垂线交l2于点A2，过点A2作y轴的垂线交l1于点A3，过点A3作x轴的垂线交l2于点A4，…依次进行下去，则点A2019的横坐标为 ．
三、解答题：本大题共7小题，共62分．解答要写出必要的文字说明、证明过程或演算步骤．
19．（8分）（1）计算：（）﹣1+（3.14﹣π）0+|2﹣|+2sin45°﹣；
（2）化简求值：（﹣）÷，当a＝﹣1时，请你选择一个适当的数作为b的值，代入求值．
20．（8分）为庆祝建国70周年，东营市某中学决定举办校园艺术节．学生从“书法”、“绘画”、“声乐”、“器乐”、“舞蹈”五个类别中选择一类报名参加．为了了解报名情况，组委会在全校随机抽取了若干名学生进行问卷调查，现将报名情况绘制成如图所示的不完整的统计图．请你根据统计图中所提供的信息解答下列问题：
（1）在这次调查中，一共抽取了多少名学生？
（2）补全条形统计图；
（3）在扇形统计图中，求“声乐”类对应扇形圆心角的度数；
（4）小东和小颖报名参加“器乐”类比赛，现从小提琴、单簧管、钢琴、电子琴四种乐器中随机选择一种乐器，用列表法或画树状图法求出他们选中同一种乐器的概率．
21．（8分）如图，AB是⊙O的直径，点D是AB延长线上的一点，点C在⊙O上，且AC＝CD，∠ACD＝120°．
（1）求证：CD是⊙O的切线；
（2）若⊙O的半径为3，求图中阴影部分的面积．
22．（8分）如图，在平面直角坐标系中，直线y＝mx与双曲线y＝相交于A（﹣2，a）、B两点，BC⊥x轴，垂足为C，△AOC的面积是2．
（1）求m、n的值；
（2）求直线AC的解析式．
23．（8分）为加快新旧动能转换，提高公司经济效益，某公司决定对近期研发出的一种电子产品进行降价促销，使生产的电子产品能够及时售出，根据市场调查：这种电子产品销售单价定为200元时，每天可售出300个；若销售单价每降低1元，每天可多售出5个．已知每个电子产品的固定成本为100元，问这种电子产品降价后的销售单价为多少元时，公司每天可获利32000元？
24．（10分）如图1，在Rt△ABC中，∠B＝90°，AB＝4，BC＝2，点D、E分别是边BC、AC的中点，连接DE．将△CDE绕点C逆时针方向旋转，记旋转角为α．
（1）问题发现
①当α＝0°时，＝ ；②当α＝180°时，＝ ．
（2）拓展探究
试判断：当0°≤α＜360°时，的大小有无变化？请仅就图2的情形给出证明．
（3）问题解决
△CDE绕点C逆时针旋转至A、B、E三点在同一条直线上时，求线段BD的长．
25．（12分）已知抛物线y＝ax2+bx﹣4经过点A（2，0）、B（﹣4，0），与y轴交于点C．
（1）求这条抛物线的解析式；
（2）如图1，点P是第三象限内抛物线上的一个动点，当四边形ABPC的面积最大时，求点P的坐标；
（3）如图2，线段AC的垂直平分线交x轴于点E，垂足为D，M为抛物线的顶点，在直线DE上是否存在一点G，使△CMG的周长最小？若存在，求出点G的坐标；若不存在，请说明理由．
2024年山东省东营市中考数学试卷
参考答案与试题解析
一、选择题：本大题共10小题，在每小题给出的四个选项中，只有一项是正确的，请把正确的选项选出来．每小题选对得3分，选错、不选或选出的答案超过一个均记零分．
1．【解答】解：﹣2019的相反数是：2019．
故选：B．
2．【解答】解：A、3x3﹣5x3＝﹣2x3，故此选项错误；
B、8x3÷4x＝2x2，故此选项错误；
C、＝，正确；
D、+无法计算，故此选项错误．
故选：C．
3．【解答】解：∵BA∥EF，∠A＝30°，
∴∠FCA＝∠A＝30°．
∵∠F＝∠E＝45°，
∴∠AOF＝∠FCA+∠F＝30°+45°＝75°．
故选：A．
4．【解答】解：A、不是轴对称图形，故本选项错误；
B、不是轴对称图形，故本选项错误；
C、不是轴对称图形，故本选项错误；
D、是轴对称图形，故本选项正确．
故选：D．
5．【解答】解：设这个队胜x场，负y场，
根据题意，得．
故选：A．
6．【解答】解：画树状图得：
∵共有12种等可能的结果，任取两个不同的数，a2+b2＞19的有4种结果，
∴a2+b2＞19的概率是＝，
故选：D．
7．【解答】解：由作法得GF垂直平分BC，
∴FB＝FC，CG＝BG＝2，FG⊥BC，
∵∠ACB＝90°，
∴FG∥AC，
∴BF＝CF，
∴CF为斜边AB上的中线，
∵AB＝＝5，
∴CF＝AB＝．
故选：A．
8．【解答】解：A、由函数图象可知，甲走完全程需要82.3秒，乙走完全程需要90.2秒，甲队率先到达终点，本选项错误；
B、由函数图象可知，甲、乙两队都走了300米，路程相同，本选项错误；
C、由函数图象可知，在47.8秒时，两队所走路程相等，均无174米，本选项正确；
D、由函数图象可知，从出发到13.7秒的时间段内，甲队的速度慢，本选项错误；
故选：C．
9．【解答】解：如图将圆锥侧面展开，得到扇形ABB′，则线段BF为所求的最短路程．
设∠BAB′＝n°．
∵＝4π，
∴n＝120即∠BAB′＝120°．
∵E为弧BB′中点，
∴∠AFB＝90°，∠BAF＝60°，
∴BF＝AB•sin∠BAF＝6×＝3，
∴最短路线长为3．
故选：D．
10．【解答】解：①∵四边形ABCD是正方形，
∴OC＝OD，AC⊥BD，∠ODF＝∠OCE＝45°，
∵∠MON＝90°，
∴∠COM＝∠DOF，
∴△COE≌△DOF（ASA），
故①正确；
②∵∠EOF＝∠ECF＝90°，
∴点O、E、C、F四点共圆，
∴∠EOG＝∠CFG，∠OEG＝∠FCG，
∴OGE∽△FGC，
故②正确；
③∵△COE≌△DOF，
∴S△COE＝S△DOF，
∴，
故③正确；
④）∵△COE≌△DOF，
∴OE＝OF，又∵∠EOF＝90°，
∴△EOF是等腰直角三角形，
∴∠OEG＝∠OCE＝45°，
∵∠EOG＝∠COE，
∴△OEG∽△OCE，
∴OE：OC＝OG：OE，
∴OG•OC＝OE2，
∵OC＝AC，OE＝EF，
∴OG•AC＝EF2，
∵CE＝DF，BC＝CD，
∴BE＝CF，
又∵Rt△CEF中，CF2+CE2＝EF2，
∴BE2+DF2＝EF2，
∴OG•AC＝BE2+DF2，
故④错误，
故选：B．
二、填空题：本大题共8小题，其中11-14题每小题3分，15-18题每小题3分，共28分．只要求填写最后结果．
11．【解答】解：20000用科学记数法表示为2×104．
故答案是：2×104．
12．【解答】解：原式＝x（x﹣3）﹣（x﹣3）＝（x﹣1）（x﹣3），
故答案为：（x﹣1）（x﹣3）
13．【解答】解：由统计表可知共有：12+22+10+5+3＝52人，中位数应为第26与第27个的平均数，
而第26个数和第27个数都是1，则中位数是1．
故答案为：1．
14．【解答】解：作AD⊥BC于D，
∵AB＝AC，
∴BD＝DC，
在Rt△ABD中，∠B＝30°，
∴AD＝AB＝，
由勾股定理得，BD＝＝3，
∴BC＝2BD＝6，
∴△ABC的周长为：6+2+2＝6+4，
故答案为：6+4．
15．【解答】解：解不等式x﹣3（x﹣2）＞4，得：x＜1，
解不等式≤，得：x≥﹣7，
则不等式组的解集为﹣7≤x＜1，
故答案为：﹣7≤x＜1．
16．【解答】解：∵点M，N分别是BC，AC的中点，
∴MN＝AB，
∴当AB取得最大值时，MN就取得最大值，当AB是直径时，AB最大，
连接AO并延长交⊙O于点B′，连接CB′，
∵AB′是⊙O的直径，
∴∠ACB′＝90°．
∵∠ABC＝45°，AC＝5，
∴∠AB′C＝45°，
∴AB′＝＝＝5，
∴MN最大＝．
故答案为：．
17．【解答】解：如图，
∵△ACE是以菱形ABCD的对角线AC为边的等边三角形，AC＝2，
∴CH＝1，
∴AH＝，
∵∠ABO＝∠DCH＝30°，
∴DH＝AO＝，
∴OD＝﹣﹣＝，
∴点D的坐标是（，0）．
故答案为：（，0）．
18．【解答】解：由题意可得，
A1（1，），A2（1，﹣），A3（﹣3，﹣），A4（﹣3，3），A5（9，3），A6（9，﹣9），…，
可得A2n+1的横坐标为（﹣3）n
∵2019＝2×1009+1，
∴点A2019的横坐标为：（﹣3）1009＝﹣31009，
故答案为：﹣31009．
三、解答题：本大题共7小题，共62分．解答要写出必要的文字说明、证明过程或演算步骤．
19．【解答】解：（1）原式＝2019+1++2×﹣2
＝2020+2﹣+﹣2
＝2020；
（2）原式＝•
＝
＝，
当a＝﹣1时，取b＝2，
原式＝＝1．
20．【解答】解：（1）∵被抽到的学生中，报名“书法”类的人数有20人，
占整个被抽取到学生总数的10%，
∴在这次调查中，一共抽取了学生为：20÷10%＝200（人）；
（2）被抽到的学生中，报名“绘画”类的人数为：200×17.5%＝35（人），
报名“舞蹈”类的人数为：200×25%＝50（人）；
补全条形统计图如下：
（3）被抽到的学生中，报名“声乐”类的人数为70人，
∴扇形统计图中，“声乐”类对应扇形圆心角的度数为：×360°＝126°；
（4）设小提琴、单簧管、钢琴、电子琴四种乐器分别为A、B、C、D，
画树状图如图所示：
共有16个等可能的结果，小东和小颖选中同一种乐器的结果有4个，
∴小东和小颖选中同一种乐器的概率为＝．
21．【解答】（1）证明：连接OC．
∵AC＝CD，∠ACD＝120°，
∴∠A＝∠D＝30°．
∵OA＝OC，
∴∠ACO＝∠A＝30°．
∴∠OCD＝∠ACD﹣∠ACO＝90°．即OC⊥CD，
∴CD是⊙O的切线．
（2）解：∵∠A＝30°，
∴∠COB＝2∠A＝60°．
∴S扇形BOC＝，
在Rt△OCD中，CD＝OC，
∴，
∴，
∴图中阴影部分的面积为．
22．【解答】解：（1）∵直线y＝mx与双曲线y＝相交于A（﹣2，a）、B两点，
∴点A与点B关于原点中心对称，
∴B（2，﹣a），
∴C（2，0）；
∵S△AOC＝2，
∴×2×a＝2，解得a＝2，
∴A（﹣2，2），
把A（﹣2，2）代入y＝mx和y＝得﹣2m＝2，2＝，解得m＝﹣1，n＝﹣4；
（2）设直线AC的解析式为y＝kx+b，
∵直线AC经过A、C，
∴，解得
∴直线AC的解析式为y＝﹣x+1．
23．【解答】解：设降价后的销售单价为x元，则降价后每天可售出[300+5（200﹣x）]个，
依题意，得：（x﹣100）[300+5（200﹣x）]＝32000，
整理，得：x2﹣360x+32400＝0，
解得：x1＝x2＝180．
180＜200，符合题意．
答：这种电子产品降价后的销售单价为180元时，公司每天可获利32000元．
24．【解答】解：（1）①当α＝0°时，
∵Rt△ABC中，∠B＝90°，
∴AC＝＝＝2，
∵点D、E分别是边BC、AC的中点，
∴AE＝AC＝，BD＝BC＝1，
∴＝．
②如图1﹣1中，
当α＝180°时，
可得AB∥DE，
∵＝，
∴＝＝．
故答案为：①，②．
（2）如图2，
当0°≤α＜360°时，的大小没有变化，
∵∠ECD＝∠ACB，
∴∠ECA＝∠DCB，
又∵＝＝，
∴△ECA∽△DCB，
∴＝＝．．
（3）①如图3﹣1中，当点E在AB的延长线上时，
在Rt△BCE中，CE＝，BC＝2，
∴BE＝＝＝1，
∴AE＝AB+BE＝5，
∵＝，
∴BD＝＝．
②如图3﹣2中，当点E在线段AB上时，
易知BE＝1，AE＝4﹣1＝3，
∵＝，
∴BD＝，
综上所述，满足条件的BD的长为．
25．【解答】解：（1）∵抛物线y＝ax+bx﹣4经过点A（﹣2，0），B（4，0），
∴，
解得，
∴抛物线解析式为y＝x2﹣x﹣4；
（2）如图1，连接OP，设点P（x，），其中﹣4＜x＜0，四边形ABPC的面积为S，由题意得C（0，﹣4），
∴S＝S△AOC+S△OCP+S△OBP
＝+，
＝4﹣2x﹣x2﹣2x+8，
＝﹣x2﹣4x+12，
＝﹣（x+2）2+16．
∵﹣1＜0，开口向下，S有最大值，
∴当x＝﹣2时，四边形ABPC的面积最大，
此时，y＝﹣4，即P（﹣2，﹣4）．
因此当四边形ABPC的面积最大时，点P的坐标为（﹣2，﹣4）．
（3），
∴顶点M（﹣1，﹣）．
如图2，连接AM交直线DE于点G，此时，△CMG的周长最小．
设直线AM的解析式为y＝kx+b，且过点A（2，0），M（﹣1，﹣），
∴，
∴直线AM的解析式为y＝﹣3．
在Rt△AOC中，＝2．
∵D为AC的中点，
∴，
∵△ADE∽△AOC，
∴，
∴，
∴AE＝5，
∴OE＝AE﹣AO＝5﹣2＝3，
∴E（﹣3，0），
由图可知D（1，﹣2）
设直线DE的函数解析式为y＝mx+n，
∴，
解得：，
∴直线DE的解析式为y＝﹣﹣．
∴，
解得：，
∴G（）．
时间（小时）
0.5
1
1.5
2
2.5
人数（人）
12
22
10
5
3