人教版（2024）七年级下册（2024）7.1.1 两条直线相交教学演示ppt课件

这是一份人教版（2024）七年级下册（2024）7.1.1 两条直线相交教学演示ppt课件，共23页。PPT课件主要包含了学习目标，新课导入，你发现了什么，进行新课，探究1，概念引入，邻补角的性质，邻补角互补，符号语言，特别提醒等内容，欢迎下载使用。
1.理解邻补角和对顶角的概念，能在图形中辨认.2.掌握邻补角和对顶角的性质.3.通过在图形中辨认邻补角和对顶角，培养学生的识图能力.
观察下列图片，说一说直线与直线的位置关系.
直线与直线相交于一点并形成了四个角.
如图，取两根木条a，b，将它们钉在一起，并把它们想象成两条直线，就得到一个相交线的模型. 在转动木条的过程中，它们所成的角也在变化.
问题1：两条相交的直线形成了几个角？
问题2：这些角之间有怎样的位置关系？
问题3：这些角之间有怎样的数量关系？
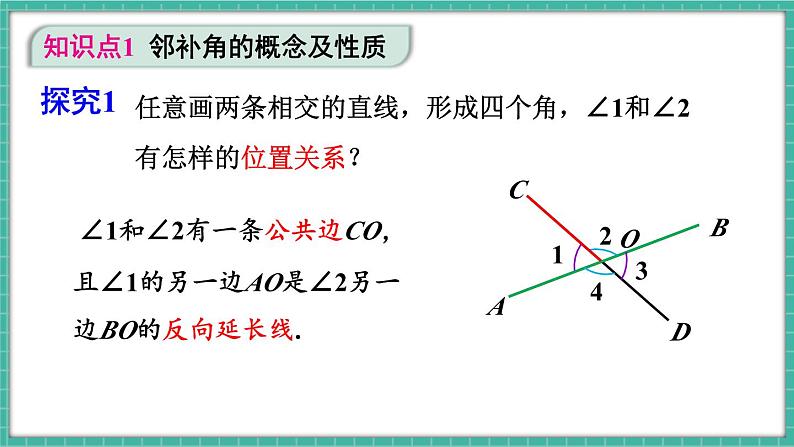
任意画两条相交的直线，形成四个角，∠1和∠2有怎样的位置关系？
∠1和∠2有一条公共边CO，
且∠1的另一边AO是∠2另一边BO的反向延长线.
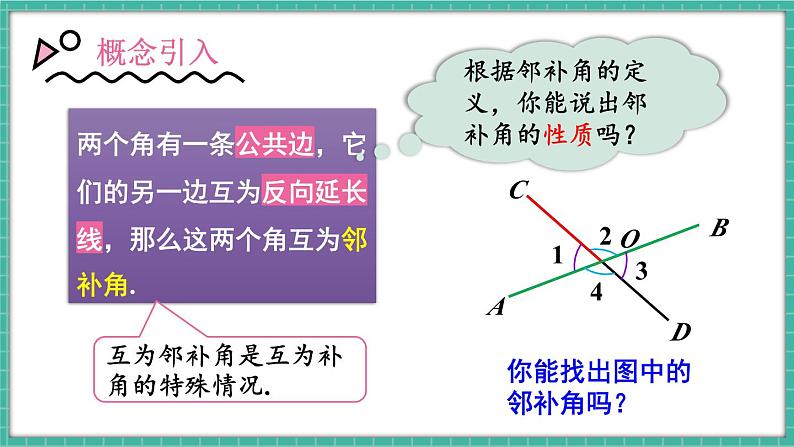
两个角有一条公共边，它们的另一边互为反向延长线，那么这两个角互为邻补角.
互为邻补角是互为补角的特殊情况.
根据邻补角的定义，你能说出邻补角的性质吗？
你能找出图中的邻补角吗？
邻补角有什么数量关系？
∠1+∠2=180°，∠2+∠3=180°，∠3+∠4=180°，∠4+∠1=180°.
因为∠1和∠2互为邻补角，所以∠1+∠2=180°.
（1）邻补角是成对出现的，单独的一个角或三个及以上的角不能称为邻补角.（2）一个角的补角可以有多个，而两直线相交时，一个角的邻补角只有两个.（3）互为邻补角的两个角一定互补，但互补的两个角不一定互为邻补角. 两个角互为邻补角，既有位置关系，又有数量关系.
练一练 下列图形中，∠1与∠2互为邻补角的是（ ）
【提示】判断两个角是否互为邻补角，首先观察两个角是否有公共边,再看另外一条边是否互为反向延长线.
∠1和∠3有怎样的位置关系？
∠1和∠3有一个公共顶点O，
且∠1的两边AO、CO分别是∠3的两边BO、DO的反向延长线.
两个角有一个公共顶点，并且其中一个角的两边分别是另一个角的两边的反向延长线，那么这两个角互为对顶角.
用量角器量出∠1和∠3的度数，你有什么发现？
你能找出图中的对顶角吗？
对顶角有什么数量关系？
∠1=∠3，∠2=∠4 .
因为∠1和∠3互为对顶角，所以∠1=∠3.
已知：直线 AB 与 CD 相交于 O 点.证明：∠1=∠3.
解：因为直线 AB 与 CD 相交于 O 点， 所以∠1与∠2互补， ∠3与∠2互补， 所以∠1=∠3（同角的补角相等）. 同理可得∠2=∠4.
（1）对顶角是成对出现的，单独的一个角或三个及以上的角不能称为对顶角.（2）互为对顶角的两个角一定相等，但相等的两个角不一定互为对顶角. 两个角互为对顶角，既有数量关系，又有位置关系.
练一练 下列图形中，∠1与∠2互为对顶角的是（ ）
【提示】判断两个角是否互为对顶角，首先看两个角有没有公共顶点，再看这两个角的两边是否互为反向延长线.
例1 如图，直线a，b相交，∠1=40°，求∠2，∠3，∠4的度数.
解：由∠1和∠2互为邻补角，得 ∠2=180°-∠1=180°-40°=140°.由对顶角相等，得 ∠3=∠1=40°，∠4=∠2=140°.
【选自教材P3“练习”】
1.下列各图中，∠1和∠2是不是对顶角？
2.如图，在相交线的模型中，如果两根木条a，b所成的角中有一个角∠α=35°，其他三个角分别等于多少度？如果∠α等于90°，115°，m°呢？
如果∠α=35°，其他三个角分别是145°，35°，145°； ∠α=90°，其他三个角都是90°； ∠α=115°，其他三个角分别是65°，115°，65°；∠α=m°，其他三个角分别是（180－m）°，m°，（180－m）°.
3.如图，直线AB，CD相交于点O，∠AOC：∠BOC=2：7，则∠BOC=______°，∠AOD=______°