人教版八年级上册数学期末复习：选择压轴题 专题练习题（含答案解析）

这是一份人教版八年级上册数学期末复习：选择压轴题 专题练习题（含答案解析），共30页。
A．12m°B．12n°C．12m°−n°D．12m°−n°
2．如图，在△ABC中，延长CA至点F，使得AF=CA，延长AB至点D，使得BD=2AB，延长BC至点E，使得CE=3CB，连接EF、FD、DE，若S△DEF=36，则S△ABC为（ ）

A．1B．2C．3D．4
3．如图，在△ABC中，AE平分∠BAC，AD⊥BC于点D．∠ABD的角平分线BF所在直线与射线AE相交于点G，若∠ABC=2∠C，且∠G=25°，则∠DFB的度数是（ ）
A．55°B．65°C．70°D．50°
4．如图，△ABC的两条高AD与BE交于点O，AD=BD，AC=7．点F在射线BC上，且CF=AO，动点P从点O出发，沿线段OB以每秒1个单位长度的速度向终点B运动，同时动点Q从点A出发，沿射线AC以每秒3个单位长度的速度运动，当点P到达点B时，P，Q两点同时停止运动，设运动时间为t秒，当△AOP与△FCQ全等时，则t的值为（ ）
A．74秒B．76秒C．74秒或76秒D．74秒或72秒
5．如图所示，锐角△ABC中，D，E分别是AB，AC边上的点，△ADC≌△ADC′，△AEB≌△AEB′，且C′D//EB′//BC，BE、CD交于点F，若∠BAC=40°，则∠BFC的大小是（ ）

A．105°B．100°C．110°D．115°
6．如图，正方形EGMP和正方形FNHP的顶点E、F、G、M、N在长方形ABCD的边上．已知DM=54DN=20，BE+CF=EF，则长方形ABCD的面积为（ ）
A．320B．480C．640D．800
7．如图，在△ADE和△ABC中，∠E=∠C，DE=BC，AE=AC，过A作AF⊥DE，垂足为F，DE交CB的延长线于点G，连接AG．四边形DGBA的面积为64，AF=8．则FG的长是（ ）
A．8B．152C．203D．6
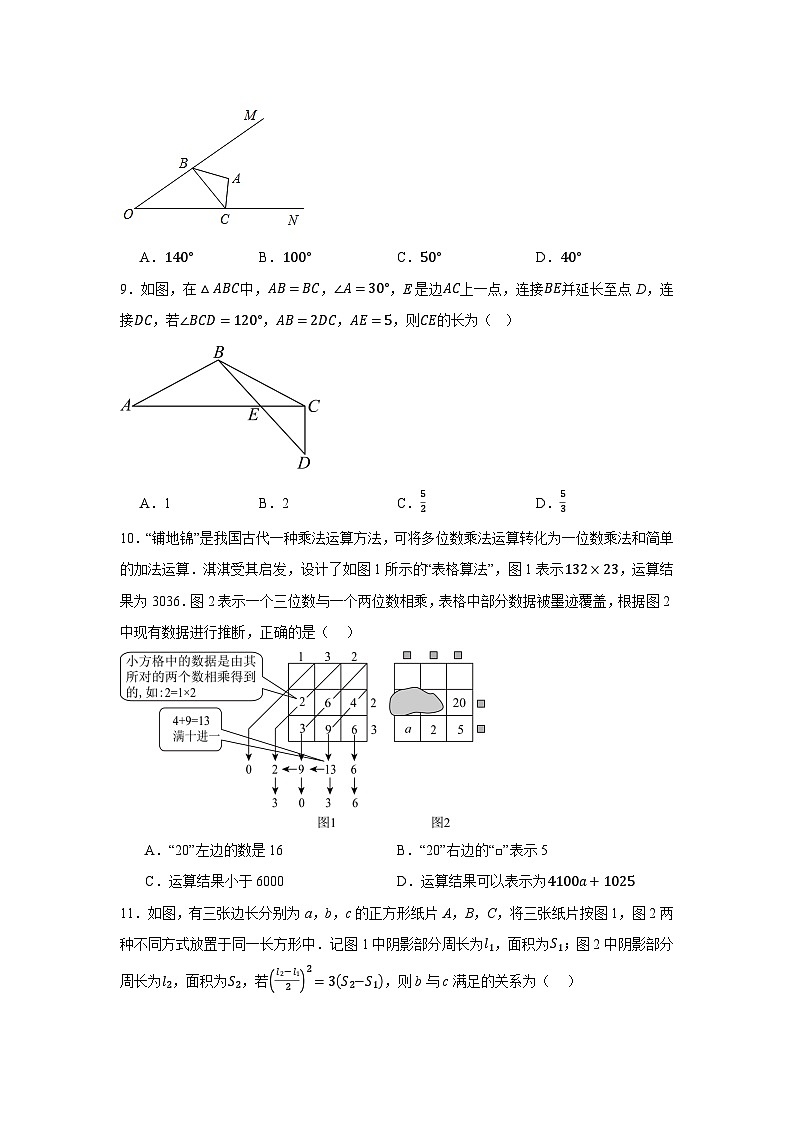
8．已知∠MON=40°，点A是∠MON内任意一点，点B和点C分别是射线OM和射线ON上的动点（M、N不与点O重合），当△ABC周长取最小值时，则∠BAC的度数为（ ）
A．140°B．100°C．50°D．40°
9．如图，在△ABC中，AB=BC，∠A=30°，E是边AC上一点，连接BE并延长至点D，连接DC，若∠BCD=120°，AB=2DC，AE=5，则CE的长为（ ）
A．1B．2C．52D．53
10．“铺地锦”是我国古代一种乘法运算方法，可将多位数乘法运算转化为一位数乘法和简单的加法运算．淇淇受其启发，设计了如图1所示的“表格算法”，图1表示132×23，运算结果为3036．图2表示一个三位数与一个两位数相乘，表格中部分数据被墨迹覆盖，根据图2中现有数据进行推断，正确的是（ ）
A．“20”左边的数是16B．“20”右边的“□”表示5
C．运算结果小于6000D．运算结果可以表示为4100a+1025
11．如图，有三张边长分别为a，b，c的正方形纸片A，B，C，将三张纸片按图1，图2两种不同方式放置于同一长方形中．记图1中阴影部分周长为l1，面积为S1；图2中阴影部分周长为l2，面积为S2，若 l2− l122=3S2−S1，则b与c满足的关系为（ ）
A．3b=5cB．b=2cC．3b=7cD．6b=7c
12．已知m，n均为正整数且满足mn−3m−2n−24=0，则m＋n的最大值是（ ）
A．16B．22C．34D．36
13．已知x2−3x+1=0，则x3−5x+1x2的值为（ ）
A．4B．5C．±4D．±5
14．我国是一个水资源贫乏的国家，每一个公民都应自觉养成节约用水的意识和习惯，为提高水资源的利用率，某住宅小区安装了循环用水装置．经测算，原来a天用水b吨，现在这些水可多用4天，现在每天比原来少用水（ ）
A．4ba吨B．4aba+4吨C．4ba(a+4)吨D．4aba(a+4)吨
15．若关于x的一元一次不等式组−5−x≤111x−a3x+12>2x+1恰好有3个整数解，且关于y的分式方程2y−ay−1−3y−21−y=1有非负整数解，则符合条件的所有整数a的和为（ ）
A．6B．9C．−1D．2
16．若a=3b且a、b为正整数，当分式方程a2x+3−b−xx−5=1的解为整数时，所有符合条件的b的值和为（ ）
A．277B．240C．272D．256
17．若关于x的方程1x−1+mx−2=2m+2(x−1)(x−2)无解，则m的值为（ ）
A．−32或−1B．−2或0
C．−32或−2或0D．−32或−2或−1
18．甲、乙、丙三名打字员承担一项打字任务，已知如下信息：
如果每小时只安排1名打字员，那么按照甲、乙、丙的顺序至完成工作任务，共需（ ）
A．1316小时B．1312小时C．1416小时D．1412小时
19．如图，在△ABC中，∠BAC=90°，AD是高，BE是中线，CF是角平分线，CF交AD于点G，交BE于点H．下列结论：①S△ABE=S△BCE；②∠AFG=∠AGF；③∠EBC=∠HCB；④∠FAG=2∠ACF，其中错误的是（ ）
A．①B．②C．③D．④
20．如图，AD、CF分别是△ABC的高和角平分线，AD与CF相交于G，AE平分∠CAD交BC于E，交CF于M，连接BM交AD于H，且BM⊥AE，有以下结论中：①∠AMC=135°；②△AMH≌△BME；③BC=BH+2MH；④AH+CE=AC．正确的结论个数有（ ）
A．1个B．2个C．3个D．4个
21．如图，在四边形ABCD中，AB=AD，∠BAD=150°，AB⊥CB于点B，AD⊥CD于点D，E、F分别是CB、CD上的点，且∠EAF=75°，EF=3，下列结论中：①△ADF≌△ABE；②EA平分∠FEB；③EF平分∠AEC；④若四边形ABCD的周长是15，且△EAF的面积为3，则四边形ABCD的面积等于11．上述结论中一定正确的有（ ）
A．①②④B．②③C．②④D．③④
22．如图，在Rt△ABC中，∠BAC=90°，CD是△ABC的角平分线，AE⊥CD于点E，连接BE，AB=6，AC=8，BC=10，则△ABE的面积是（ ）
A．95B．2C．125D．245
参考答案：
1．D
【分析】题目由于在三角形中未确定∠A、∠B大小，所以需要进行分类讨论：（1）∠A∠B时，由图可得：∠DCE=∠ACE−∠ACD，∠ACE=∠ACB2=180°−(m°+n°)2，在RtΔACD中，∠ACD=90°−∠A=90°−m°，故可得∠DCE=12(m°−n°)；综上可得：∠DCE=12m°−n°．
【详解】解：（1）如图1所示：∠A∠B时，
图2
∵CD是AB边上的高，
∴CD⊥AB，∠CDB=90°，
∵∠A=m°，∠B=n°，
∴∠ACB=180°−(m°+n°)，
∵CE平分∠ACB，
∴∠ACE=∠BCE=∠ACB2=180°−(m°+n°)2，
在RtΔACD中，∠ACD=90°−∠A=90°−m°，
∴∠DCE=∠ACE−∠ACD=180°−m°+n°2−90°−m°=12(m°−n°)；
综合（1）（2）两种情况可得：∠DCE=12m°−n°．
故选：D．
【点睛】题目主要考查对三角形分类讨论、数形结合思想，主要知识点是三角形的角平分线、高线的基本性质及图形内角的运算，题目难点是在依据题意进行分类讨论的情况下，作出相应的三角形图形．
2．B
【分析】先设△ABC的面积为m，再根据底共线，高相等，面积的比等于底边的比，将其余各个三角形的面积表示出来，总面积为36，解得△ABC的面积．
【详解】解：如图，连接EA、CD，设△ABC的面积为m，

∵ BD=2AB，
∴ △BCD的面积为2m，△ACD的面积为3m，
∵ AF=CA
∴ △AFD的面积为3m，
∵ CE=3CB,
∴ △ACE的面积为3m，△AEF的面积为3m，△ECD的面积为6m，
∴ S△DEF=m+2m+3m+3m+6m+3m=18m=36，
∴ m=2，即△ABC的面积为2
故选：B
【点睛】本题考查了三角形的面积问题，等高且共底的三角形面积比是底边的比这个性质是解题的关键．
3．D
【分析】此题主要考查了角平分线的定义，三角形的外角性质，三角形的内角和定理， 直角三角形的性质，设∠CAE=α，根据角平分线的定义得∠BAE=∠CAE=α，∠BAC=2∠CAE=2α，由三角形的外角定理得∠ABD=∠BAC+∠C=2α+∠C，则∠ABF=∠DBF=12∠ABD=α+12∠C，同时∠ABF=∠BAE+∠G=α+25°，由此得∠C=50°，则∠ABC=2∠C=100°，进而得∠ABD=180°−∠ABC=80°，∠DBF=12∠ABD=40°，然后再根据AD⊥BC可得∠DFB的度数，熟练掌握三角形的外角定理和三角形的内角和定理是解题的关键．
【详解】解：设∠CAE=α，
∵AE平分∠BAC，
∴∠BAE=∠CAE=α，∠BAC=2∠CAE=2α，
∵∠ABD是△ABC的外角，
∴∠ABD=∠BAC+∠C=2α+∠C，
∵BF平分∠ABD，
∴∠ABF=∠DBF=12∠ABD=α+12∠C
∵∠ABF是△ABG的外角，∠G=25°，
∴∠ABF=∠BAE+∠G=α+25°，
∴α+12∠C=α+25°，
∴∠C=50°，
∴∠ABC=2∠C=100°，
∴∠ABD=180°−∠ABC=80°，
∴∠DBF=12∠ABD=40°，
∵AD⊥BC，
∴∠ADB=90°，
∴∠DFB=90°−∠DBF=90°−40°=50°，
故选：D．
4．D
【分析】本题考查全等三角形的性质和判定，一元一次方程的应用，熟练掌握以上知识是解题的关键．
分情况讨论点分别点F在BC延长线上或在BC之间时，△AOP≌△FCQ，根据对应边相等，解一元一次方程求得t值即可选出结果．
【详解】解：①当点F在BC延长线上时：设t秒时，P、Q分别运动到如图位置，△AOP≌△FCQ．
，
∵CF=AO，∠AOP=∠EOD=180°−∠DCE=∠FCQ，
∴当△AOP≌△FCQ时，OP=CQ，
∵OP=t，CQ=AC−AQ=7−3t，
∴t=7−3t，
解得t=74．
②当点F在BC之间时：设t秒时，P、Q分别运动到如图位置，△AOP≌△FCQ．
∵CF=AO，∠AOP=∠EOD=180°−∠DCE=∠FCQ，
∴当△AOP≌△FCQ时，OP=CQ，
∵OP=t，CQ=AC−AQ=3t−7，
∴t=3t−7，
解得t=72．
综上，t=74或t=72，
故选D．
5．B
【分析】延长C′D交AB′于H．利用全等三角形的性质，平行线的性质，三角形的外角的性质证明∠BFC=∠C′+∠AHC′+∠CAD，再求出∠C′+∠AHC′即可解决问题．
【详解】解：延长C′D交AB′于H．

∵△AEB≌△AEB′，
∴∠ABE=∠B′，∠EAB=∠EAB′=40°，
∵C′H∥EB′，
∴∠AHC′=∠B′，
∵△ADC≌△ADC′，
∴∠C′=∠ACD，∠DAC=∠DAC′=40°，
∵∠BFC=∠DBF+∠BDF，∠BDF=∠CAD+∠ACD，
∴∠BFC=∠AHC′+∠C′+∠CAD，
∵∠DAC=∠DAC′=∠CAB′=40°，
∴∠C′AH=120°，
∴∠C′+∠AHC′=60°，
∴∠BFC=60°+40°=100°，
故选：B．
【点睛】本题考查了全等三角形的性质，平行线的性质，三角形的内角和定理以及三角形外角的性质等知识，熟练掌握基本性质是解题的关键．
6．C
【分析】本题考查了正方形的性质，长方形的性质，全等三角形的判定与性质，熟练掌握以上知识点是解题的关键．过点P作PK⊥BC于点K，先证△PKF≌△FCN，得出KF=CN，PK=FC，同理可证△PKE≌△EBG≌△GAM，得出PK=EB=GA，EK=GB=MA，设KF=CN=x，EK=GB=MA=y，表示AD、BC、AB、CD的长，得到2x+y=20，x−3y=−32，解方程组即可，从而求出长方形的面积．
【详解】解：过点P作PK⊥BC于点K，
∴∠PFK+∠KPF=90°
∵四边形FNHP是正方形
∴PF=FN，∠PFN=90°
∴∠PFK+∠CFN=90°
∴∠KPF=∠CFN
∵四边形ABCD是长方形
∴∠C=90°，AB=CD，AD=BC
∴∠PKF=∠C=90°
在△PKF和△FCN中
∠KPF=∠CFN∠PKF=∠CPF=FN
∴△PKF≌△FCNAAS
∴KF=CN，PK=FC
同理可证△PKE≌△EBG≌△GAM
∴PK=EB=GA，EK=GB=MA
设KF=CN=x，EK=GB=MA=y
∵DM=54DN=20
∴DN=16
∴CD=DN+CN=16+x，AD=AM+DM=y+20
∵BE+CF=EF
∴EK+KF=EF，AD=BC=BE+CF+EF=2EF
∴EF=x+y
∴y+20=2x+y，即2x+y=20①
∵AB=GA+BG=AG+y，CD=16+x，AB=CD
∴GA+y=16+x
∴GA=16+x−y=PK=EB=FC
∵EB=EF−FC=x+y−16+x−y=2y−8
∵EB=GA
∴2y−16=16+x−y，即x−3y=−32②
联立①②，解得：x=4，y=12
∴AD=y+20=12+20=32，CD=16+x=16+4=20
∴S长方形ABCD=AD⋅CD=32×20=640
故选：C．
7．A
【分析】过点A作AH⊥BC于点H，利用SAS可证得△ABC≌△ADE，于是可得AD=AB，利用三角形的面积公式可得AF=AH，利用HL可证得Rt△AFG≌Rt△AHG，于是可得S△AFG=S△AHG，同理可证得Rt△AFD≌Rt△AHB，于是可得S△AFD=S△AHB，于是可推出S四边形DGBA=S△AFD+S△AFG+S△AGB=2S△AFG=64，因而可得S△AFG=32=12⋅FG⋅AF，据此即可求出FG的长．
【详解】解：如图，过点A作AH⊥BC于点H，
在△ABC和△ADE中，
AC=AE∠C=∠EBC=DE，
∴△ABC≌△ADESAS，
∴AD=AB，
又∵AF⊥DE，
∴12⋅DE⋅AF=12⋅BC⋅AH，
∴AF=AH，
∵AF⊥DE，AH⊥BC，
∴∠AFG=∠AHG=90°，
在Rt△AFG和Rt△AHG中，
AF=AHAG=AG，
∴Rt△AFG≌Rt△AHGHL，
∴S△AFG=S△AHG，
同理：Rt△AFD≌Rt△AHBHL，
∴S△AFD=S△AHB，
∴S四边形DGBA=S△AFD+S△AFG+S△AGB
=S△AHB+S△AHG+S△AGB
=S△AHG+S△AHB+S△AGB
=S△AHG+S△AHG
=2S△AHG
=2S△AFG
=64，
∴S△AFG=32=12⋅FG⋅AF，
∴FG=32×2AF=32×28=8，
故选：A．
【点睛】本题主要考查了全等三角形的判定与性质（SAS和HL），三角形的面积公式，等式的性质2，垂线的性质等知识点，添加适当辅助线构造全等三角形是解题的关键．
8．B
【分析】分别作点A关于OM、ON的对称点A1、A2，连接A1A2，交OM于B，交ON于C，△ABC的周长的最小值=A1A2，然后得到等腰△OA1A2中，∠OA1A2+∠OA2A1=100°，即可得出∠BAC=∠OAB+∠OAC=∠OA1B+∠OA2C=100°．
【详解】分别作点A关于OM、ON的对称点A1、A2，连接A1A2，交OM于B，交ON于C，
则OA1=OA=OA2，∠OA1B=∠BAO，∠CAO=∠CA2O，
根据对称轴的性质，可得BA=A1B，AC=A2C，
则△ABC的周长的最小值=A1A2，
∴∠A1OA2=2∠MON=80°，
∴等腰△OA1A2中，
∠OA1A2+∠OA2A1=100°，
∴∠BAC=∠OAB+∠OAC=∠OA1B+∠OA2C=100°．
故选：B．
【点睛】本题考查了轴对称－最对路线问题，正确作出辅助线，得到等腰△OA1A2中，∠OA1A2+∠OA2A1=100°是关键．凡是涉及最短距离的问题，一般要考虑线段的性质定理，多数情况要作点关于某直线的对称点．
9．D
【分析】作BM⊥AC，垂足为M，根据等腰三角形的性质可得∠A=∠ACB=30°，AM=CM，根据含30度角的直角三角形的性质得出BM=12AB，那么可证BM=CD．再利用AAS证明△MEB≌△CED，得出ME=CE，设CE=x，根据AM=CM列出方程，求解即可．
【详解】解：作BM⊥AC，垂足为M，则∠BMC=90°，如图所示：
∵AB=BC，∠ABC=120°，
∴∠A=∠ACB=30°，AM=CM，
∴BM=12AB，
∵AB=2CD，
∴BM=CD．
∵∠DCB=120°，
∴∠DCE=∠DCB−∠ACB=120°−30°=90°，
∴∠BMC=∠DCE=90°．
在△EMB和△ECD中，
∠BME=∠DCE∠BEM=∠DECBM=DC，
∴△MEB≌△CEDAAS，
∴ME=CE．
设CE=x，则ME=x，AM=AE−ME=5−x．
∵AM=CM，
∴5−x=2x，
∴x=53，
∴线段CE长为53．
故选：D．
【点睛】本题考查了等腰三角形的性质、含30度角的直角三角形的性质、全等三角形的判定和性质，解题的关键是添加辅助线构造全等三角形，属于中考常考题型．
10．D
【分析】本题考查了整式的加法运算，整式的乘法运算，理解题意，正确的逻辑推理时解决本题的关键．
设一个三位数与一个两位数分别为100x+10y+z和10m+n，则mz=20,nz=5,ny=2,nx=a，即m=4n，可确定n=1,y=2时，则m=4,z=5,x=a，由题意可判断A、B选项，根据题意可得运算结果可以表示为：10004a+1+100a+25=4100a+1025，故可判断C、D选项．
【详解】解：设一个三位数与一个两位数分别为100x+10y+z和10m+n
如图：
则由题意得：
mz=20,nz=5,ny=2,nx=a，
∴mznz=4，即m=4n，
∴当n=2,y=1时，z=2.5不是正整数，不符合题意，故舍；
当n=1,y=2时，则m=4,z=5,x=a，如图：
，
∴A、“20”左边的数是2×4=8，故本选项不符合题意；
B、“20”右边的“□”表示4，故本选项不符合题意；
∴a上面的数应为4a，如图：
∴运算结果可以表示为：10004a+1+100a+25=4100a+1025，
∴D选项符合题意，
当a=2时，计算的结果大于6000，故C选项不符合题意，
故选：D．
11．C
【分析】本题考查了整式混合运算在面积中的应用，分别用含a，b，c的式子表示出l1，l2，S1，S2，代入 l2− l122=3S2−S1进行运算，即可求解；能表示出各个量，正确进行整式运算是解题的关键．
【详解】解：由图可知，长方形的长为a+b，宽为a+c，
l1=a+b−c+a−c+b+c+a−b+a+c−b=4a，
S1=a+ba+c−a2−b2−c2=ab+ac−b2+bc−c2，
l2=2a+2c+2b+2a+c−b=4a+c，
S2=ba+c−b+cb−c+ca−c=ab+ac−b2+2bc−2c2，
∴S2−S1=bc−c2，l2−l1=4c，
∵ l2− l122=3S2−S1，
∴4c2=3bc−c2，
解得b=7c3，即3b=7c，
故选：C．
12．D
【分析】由mn−3m−2n−24=0得(m−2)(n−3)=30.由于30=1×30=2×15=3×10=5×6 =30×1=15×2=10×3=6×5，据此列出关于m、n的方程组，求出每一组m、n的值，再求出相应的m＋n的值，即可找到m＋n的最大值.
【详解】由mn−3m−2n−24=0得
mn−3m−2n+6−30=0
m(n−3)−2(n−3)=30
(m−2)(n−3)=30
∵m，n均为正整数
∴m−2=1n−3=30或m−2=2n−3=15或m−2=3n−3=10或m−2=5n−3=6
或m−2=30n−3=1或m−2=15n−3=2或m−2=10n−3=3 或m−2=6n−3=5
解得m=3n=33或m=4n=18或m=5n=13或m=7n=9或m=32n=4或m=17n=5或m=12n=6或m=8n=8
∴m+n=36或22或18或16
∴m＋n的最大值是36
故选：D
【点睛】本题主要考查了因式分解的应用，解题的关键是将mn−3m−2n−24=0变形为(m−2)(n−3)=30.
13．B
【分析】将x2−3x+1=0，进行变形得到：x2=3x−1，x2−3x=−1，x+1x=3，利用整体思想，将x3−5x+1x2变形为：x+1x2−4，再代值计算即可．
【详解】解：∵x2−3x+1=0，
∴x2=3x−1，x2−3x=−1，
∴x3−5x+1x2=xx2−5+1x2
=x3x−1−5+1x2
=3x2−6x+1x2
=2x2−6x+x2+1x2
=2x2−3x+x2+1x2
=−2+x2+1x2
=x−1x2
=x+1x2−4；
∵x2−3x+1=0，当x=0时，1≠0，方程不成立，
∴x≠0，
∴方程两边同除以x得：x−3+1x=0，
∴x+1x=3，
∴x+1x2−4=32−4=5，即：x3−5x+1x2=5；
故选B．
【点睛】本题考查分式求值．将已知条件进行变形，利用整体思想代入求值，是解题的关键．
14．C
【分析】分别求出原来平均每天用水吨数和现在平均每天用水吨数，用原来平均每天用水吨数减去现在平均每天用水吨数，即得．
【详解】原来a天用水b吨，原来平均每天用水ba吨，
现在这些水可多用4天，现在平均每天用水ba+4吨，
现在平均每天比原来少用水，ba−ba+4=ba+4−abaa+4=4baa+4（吨）．
故选：C．
【点睛】本题主要考查了列代数式，解决问题的关键是熟练列出用水量相同，用水时间不同的平均每天用水量的计算表达式．
15．A
【分析】本题考查了分式方程的解，一元一次不等式组的整数解，熟练掌握解一元一次不等式组，解分式方程是解题的关键．先解一元一次不等式组，根据不等式组的解集恰好有3个负整数解，求出a的范围，再解分式方程，根据分式方程有非负整数解，确定a的值即可．
【详解】解：−5−x≤111x−a①3x+12>2x+1②，
解不等式①得：x≥a−5512，
解不等式②得：xBN，即可判断结论③；综上，即可得出答案．
【详解】解：∵AD是△ABC的高，
∴∠ADC=90°，
∴∠CAD+∠ACD=90°，
∵CF是△ABC的角平分线，AE平分∠CAD，
∴∠MAC=12∠CAD，∠MCA=12∠ACD，
∴∠MAC+∠MCA=12∠CAD+12∠ACD=12∠CAD+∠ACD=12×90°=45°，
∴∠AMC=180°−∠MAC+∠MCA=180°−45°=135°，
故结论①正确；
∵AD是△ABC的高，BM⊥AE，
∴∠ADB=∠ADC=∠AMB=∠EMB=90°，
∵∠AHM=∠BHD，
∴180°−∠AMB−∠AHM=180°−∠ADB−∠BHD，
∴∠HAM=∠CBM，
∵CF是△ABC的角平分线，AE平分∠CAD，
∴∠CAM=∠HAM，∠ACM=∠BCM，
∴∠CAM=∠CBM，
在△CAM和△CBM中，
∠CAM=∠CBM∠ACM=∠BCMCM=CM，
∴△CAM≌△CBMAAS，
∴MA=MB，
在△AMH和△BME中，
∠HAM=∠EBMMA=MB∠AMH=∠BME，
∴△AMH≌△BMEASA，
故结论②正确；
∵△CAM≌△CBM，
∴AC=BC，
∵△AMH≌△BME，
∴AH=BE，
∵BE+CE=BC，
∴AH+CE=AC，
故结论④正确；
如图，延长BM交AC于点N，
∵∠AMN=180°−∠AMB=180°−90°=90°，
∴∠AMN=∠AMB=∠AMH，
在△AMH和△AMN中，
∠HAM=∠NAMMA=MA∠AMH=∠AMN，
∴△AMH≌△AMNASA，
∴MH=MN，
∴BH+2MH=BH+MH+MN=BN，
∵∠BNC=∠AMN+∠NAM=90°+∠NAM>90°，是钝角，
∴∠BNC>∠BCN，
∴BC>BN，
即：BC>BH+2MH，
故结论③错误；
综上所述，正确的结论有：①②④，共3个，
故选：C．
【点睛】本题主要考查了垂线的性质，直角三角形的两个锐角互余，三角形角平分线的定义，三角形的内角和定理，对顶角相等，等式的性质1，全等三角形的判定与性质（AAS和ASA），利用邻补角互补求角度，线段的和与差，三角形外角的性质，不等式的性质等知识点，熟练掌握全等三角形的判定与性质是解题的关键．
21．C
【分析】本题考查了全等三角形的性质和判定定理，角平分线的定义，三角形的三边关系定理，垂直定义等知识点，延长EB到G，使BG=DF，连接AG，AC，根据全等三角形的判定定理求出△ADF≌△ABG，根据全等三角形的性质得出AF=AG，∠G=∠DFA，∠DAF=∠BAG，求出∠FAE=∠EAG=75°，根据全等三角形的判定定理得出△FAE≌△GAE，根据全等三角形的性质得出∠FEA=∠GEA，∠G=∠EFA，EF=EG，再进行判断即可．
【详解】解：延长EB到G，使BG=DF，连接AG，AC，
∵AB⊥CB，AD⊥CD，
∴∠D=∠ABG=90°，
在△ADF和△ABG中
AD=AB∠D=∠ABGDF=BG，
∴△ADF≌△ABGSAS，
∴AF=AG，∠G=∠DFA，∠DAF=∠BAG，
∵∠EAF=75°，∠DAB=150°，
∴∠DAF+∠EAB=∠DAB−∠FAE=150°−75°=75°，
∴∠EAG=∠EAB+∠BAG=∠EAB+∠FAD=75°，
∴∠FAE=∠EAG=75°，
在△FAE和△GAE中
AE=AE∠FAE=∠EAGAF=AG，
∴△FAE≌△GAESAS，
∴∠FEA=∠GEA，∠G=∠EFA，EF=EG=3，
∴EA平分∠FEB，故②正确；
根据已知不能推出△ADF≌△ABE，EF平分∠AEC，故①③不正确；
在Rt△ACD和Rt△ACB中，
AC=ACAD=AB，
∴Rt△ACD≌Rt△ACBHL，
∴CD=CB，
设AD=AB=a，CD=CB=b，
∵四边形ABCD的周长是15，
∴2a+b=15，
∵△EAF的面积为3，
∴S△EAF=12EG⋅AB=12EF⋅AB=12×3×a=3，
∴a=2，
∴b=112，
∴四边形ABCD的面积=2S△ADC=2×12×ab=2×12×2⋅112=11，故④正确；
综上，正确的有②④．
故选：C．
22．C
【分析】本题考查了角平分线的定义，全等三角形的证明与性质，三角形中线的性质，熟练掌握以上知识点并作出合适的辅助线是解题的关键．延长AE交BC于点F，作AM⊥BC与点M，利用角平分线的定义可证△AEC≌△FECASA，可推出AE=EF，FC=AC=8，再根据三角形面积可求得AM，从而得到S△ABF，最后利用三角形中线的性质可知S△ABE=12S△ABF，即可求得答案．
【详解】解：延长AE交BC于点F，作AM⊥BC与点M，如图所示，
∵AE⊥CD，CD是△ABC的角平分线
∴∠AEC=∠FEC=90°，∠ACE=∠FCE
在△AEC和△FEC中
∠AEC=∠FECEC=EC∠ACE=∠FCE
∴△AEC≌△FECASA
∴AE=EF，FC=AC
∵∠BAC=90°，AB=6，AC=8，BC=10
∴ BF=BC−FC=BC−AC=10−8=2
∵S△ABC=12AB⋅AC=12BC⋅AM
∴AM=AB⋅ACBC=6×810=245
∴S△ABF=12BF⋅AM=12×2×245=245
∵AE=EF
∴S△ABE=12S△ABF=12×245=125
故选：C．
题号
1
2
3
4
5
6
7
8
9
10
答案
D
B
D
D
B
C
A
B
D
D
题号
11
12
13
14
15
16
17
18
19
20
答案
C
D
B
C
A
C
D
C
C
C
题号
21
22








答案
C
C