初中人教版（2024）17.1 勾股定理试讲课教学作业ppt课件

这是一份初中人教版（2024）17.1 勾股定理试讲课教学作业ppt课件，文件包含1712勾股定理在实际生活中的应用pptx、1712勾股定理在实际生活中的应用教学设计docx、1712勾股定理在实际生活中的应用分层作业原卷版docx、1712勾股定理在实际生活中的应用分层作业解析版docx、1712勾股定理在实际生活中的应用导学案docx等5份课件配套教学资源，其中PPT共30页， 欢迎下载使用。
1.会运用勾股定理求线段长及解决简单的实际问题.（重点）2.能从实际问题中抽象出直角三角形这一几何模型，利用勾股定理建立已知边与未知边长度之间的联系，并进一步求出未知边长.（难点）
如图，在△ABC中，AD⊥BC于点D，AB＝3，BD＝2，DC＝1，求AC的长．
解：在Rt△ABD中，AB＝3，BD＝2， 由勾股定理得AD2＝AB2－BD2＝32－22＝5. 在Rt△ACD中，CD＝1，由勾股定理得
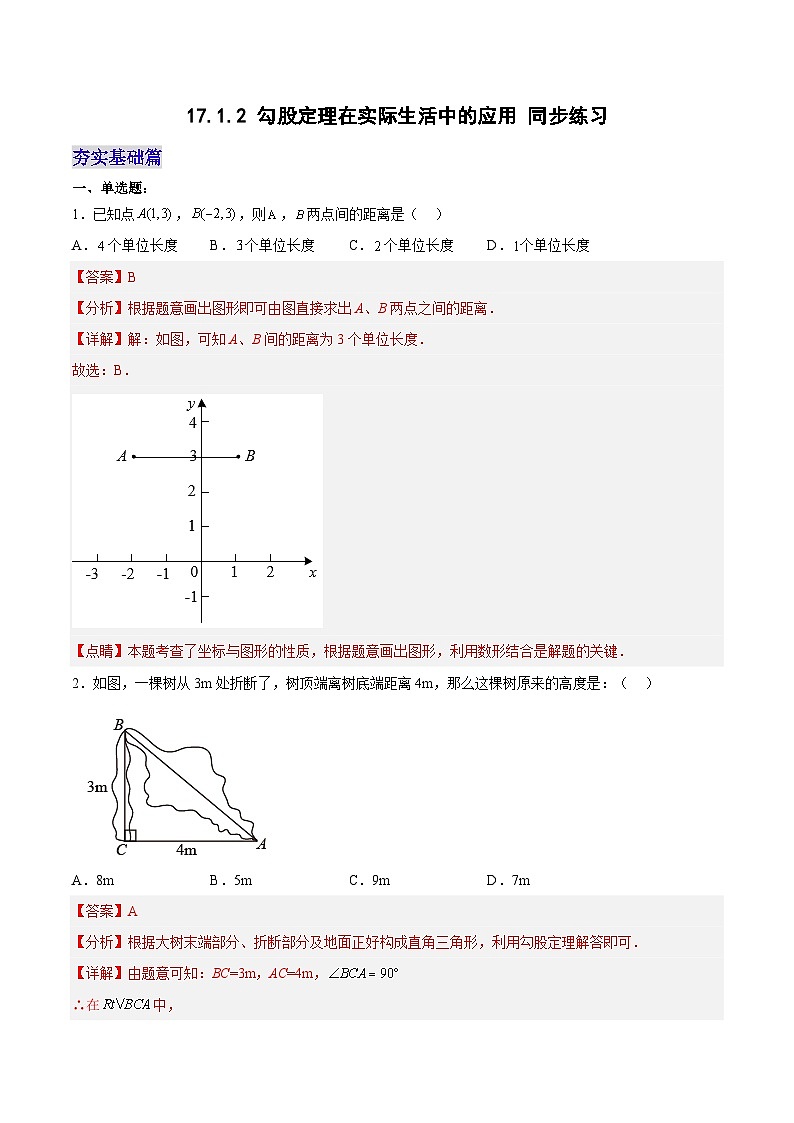
例1.一个门框的尺寸如图所示，一块长3m,宽2.2m的长方形薄木板能否从门框内通过?为什么?
分析：可以看出木板横着，竖着都不能通过，只能斜着.门框AC的长度是斜着能通过的最大长度，只要AC的长大于木板的宽就能通过.
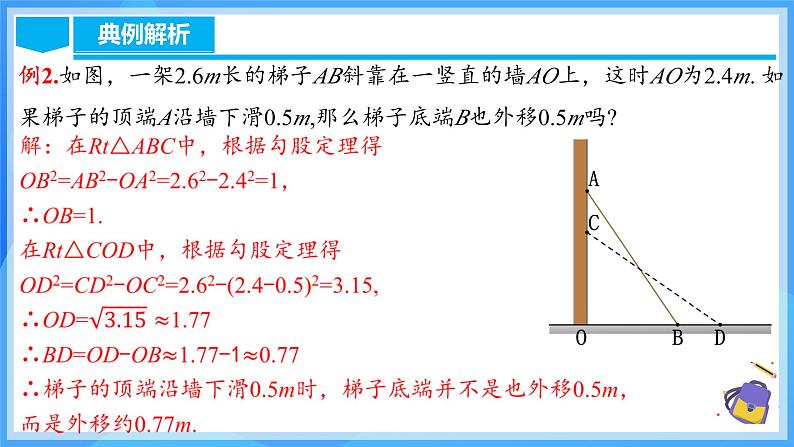
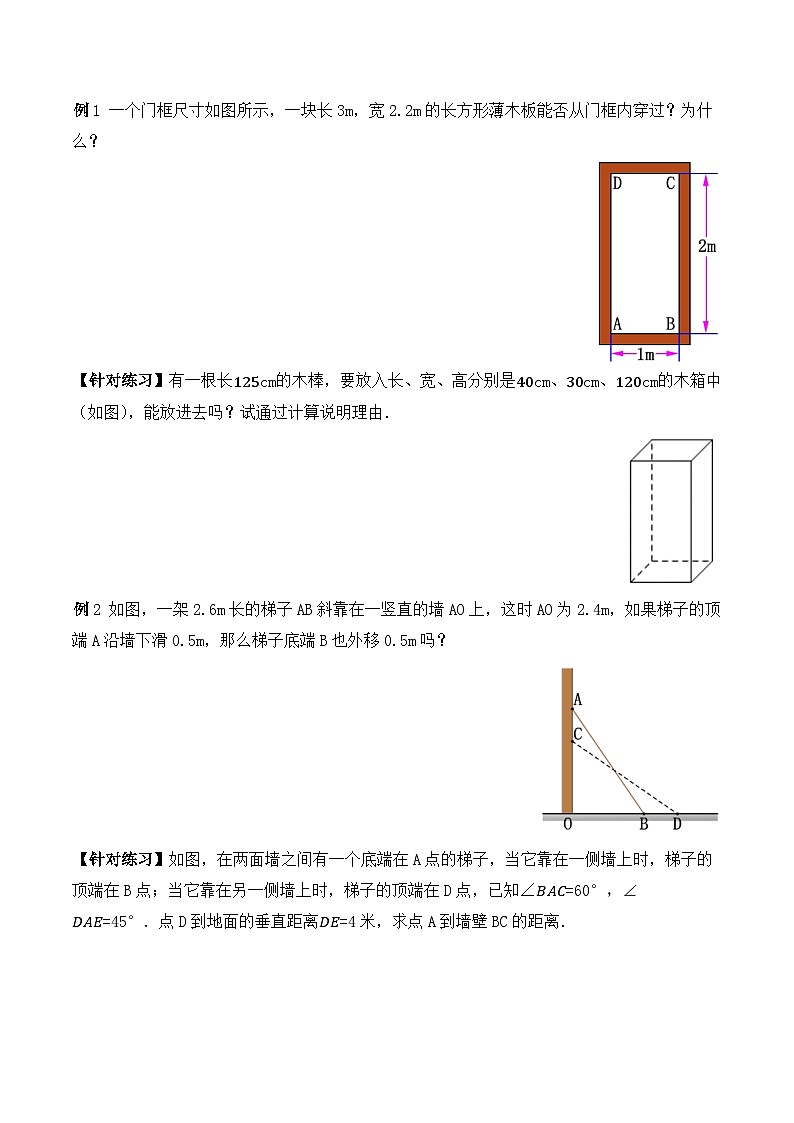
例2.如图，一架2.6m长的梯子AB斜靠在一竖直的墙AO上，这时AO为2.4m. 如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
利用勾股定理解决实际问题的一般步骤：
（1）读懂题意，分析已知、未知间的关系；
（2）构造直角三角形；
（3）利用勾股定理等列方程；
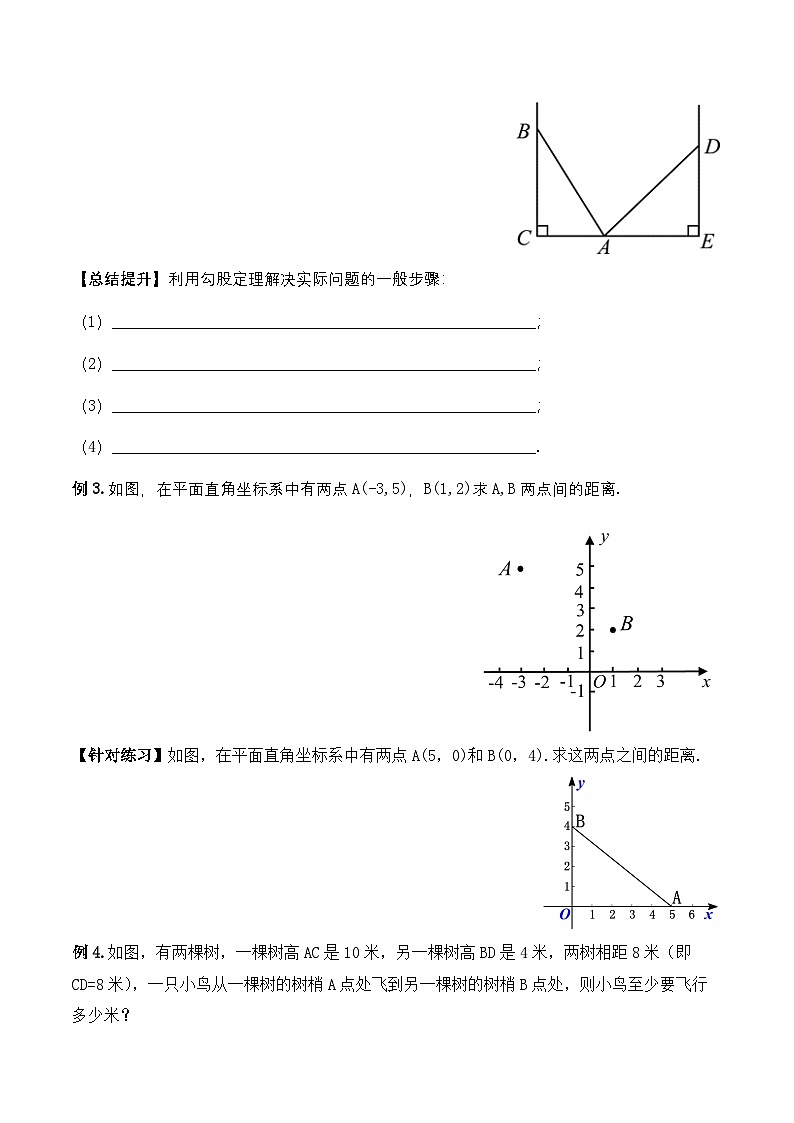
例3.如图，在平面直角坐标系中有两点A(-3,5)，B(1,2)求A,B两点间的距离.
解：如图，过点A作x轴的垂线,过点B作x,y轴的垂线.相交于点C,连接AB.∴AC=5-2=3，BC=3+1=4，在Rt△ABC中，由勾股定理得∴A,B两点间的距离为5.
【点睛】两点之间的距离公式：一般地，设平面上任意两点
如图，在平面直角坐标系中有两点A(5，0)和B(0，4).求这两点之间的距离.
例4.如图，有两棵树，一棵树高AC是10米，另一棵树高BD是4米，两树相距8米（即CD=8米），一只小鸟从一棵树的树梢A点处飞到另一棵树的树梢B点处，则小鸟至少要飞行多少米？
例5.如图，甲乙两船同时从A港出发，甲船沿北偏东35°的方向，航速是12海里/时，2小时后，两船同时到达了目的地．若C、B两岛的距离为30海里，问乙船的航速是多少？
例6.有一个圆柱形油罐，要以A点环绕油罐建梯子，正好建在A点的正上方点B处,问梯子最短需多少米(已知油罐的底面半径是2m,高AB是5m,π取3）?
解：油罐的展开图如图，则AB′为梯子的最短距离. ∵AA′=2×3×2=12, A′B′=5,在Rt△AA′B′中，由勾股定理得即梯子最短需13米.
【分析】立体图形中求两点间的最短距离，一般把立体图形展开成平面图形，连接两点，根据两点之间线段最短确定最短路线.
如图，是一个边长为1的正方体硬纸盒，现在A处有一只蚂蚁，想沿着正方体的外表面到达B处吃食物，求蚂蚁爬行的最短距离是多少.
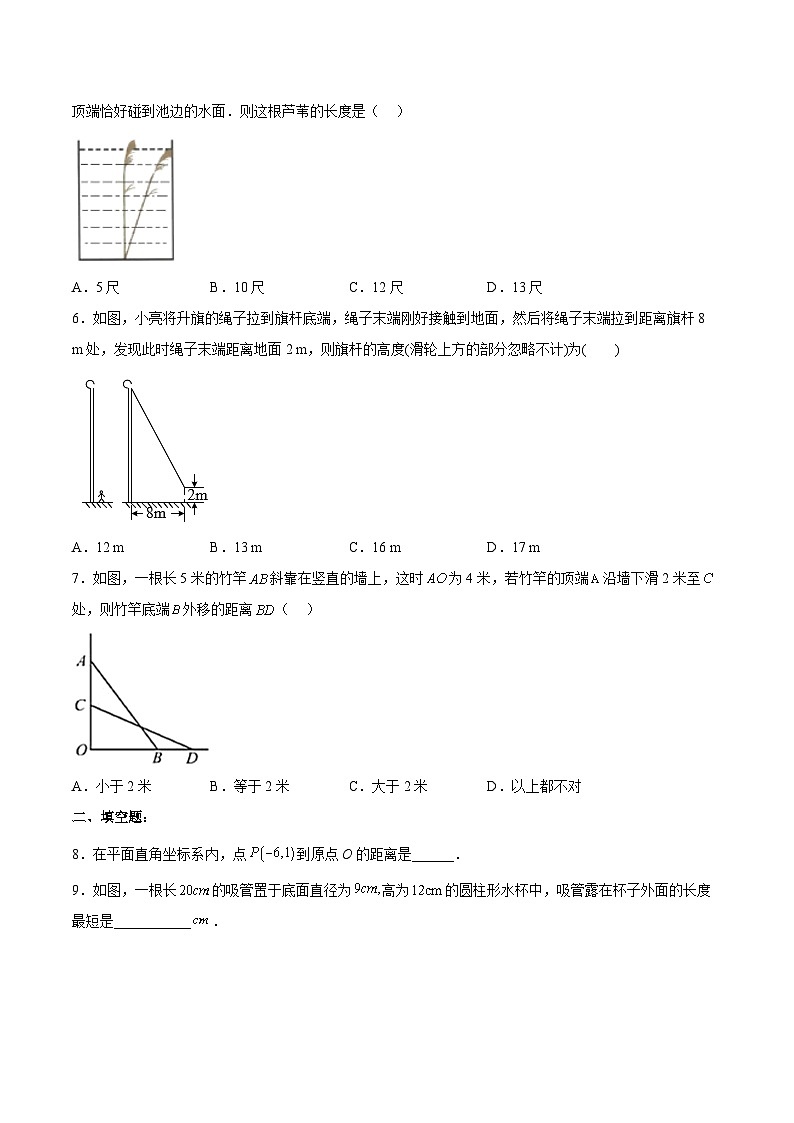
3.如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离为0.7米，顶端距离地面2.4米.如果保持梯子底端位置不动，将梯子斜靠在右墙时，顶端距离地面2米，那么小巷的宽度为( )A.0.7米 B.1.5米 C.2.2米 D.2.4米
5.如图是一个育苗棚，棚宽a=6m,棚高h=2.5m,棚长d=10m，则覆盖在棚斜面上的塑料薄膜的面积为______m2.6.如果将一根细长木棒放进长为3cm、宽为2cm、 高为6cm的长方体有盖盒子中，那么细木棒最长可以是_____cm.
7.暑假中，小明和同学们到某海岛去探宝旅游,按照如图所示的路线探宝.他们登陆后先往东走8km，又往北走2km，遇到障碍后又往西走3km，再折向北走6km处往东拐,仅走1km就找到了宝藏，则登陆点到埋宝藏点的直线距离为______km.
8.如图，池塘边有两点A、B，点C是与BA方向成直角的AC方向上一点，测得CB=60m，AC=20m.求A、B两点间的距离(结果取整数).
11.如图，有一个圆柱体，它的高为12厘米，底面半径为3厘米，在圆柱下底面的A点有一只蚂蚁，它想吃到上底面与A点相对的B处的食物，需要爬行的最短路程是多少?(π的值取3)