人教版（2024）七年级下册（2024）9.1.1 平面直角坐标系的概念教课ppt课件

这是一份人教版（2024）七年级下册（2024）9.1.1 平面直角坐标系的概念教课ppt课件，共26页。PPT课件主要包含了表示数字4的点是点C，－3－4，－20，－4－3－2－1，－1－2－3－4，第一象限，第二象限，第三象限，第四象限，－34等内容，欢迎下载使用。
在庆祝中华人民共和国成立70周年联欢活动中，天安门广场上出现了“祖国万岁”等壮观的图案，你知道它们是怎么组成的吗?
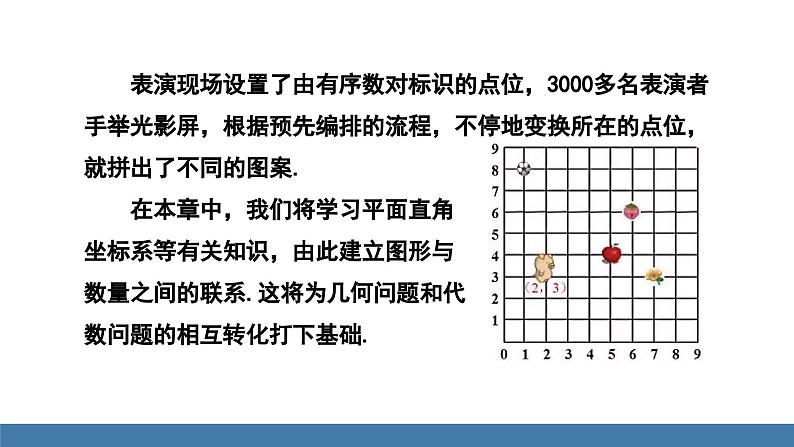
表演现场设置了由有序数对标识的点位，3000多名表演者手举光影屏，根据预先编排的流程，不停地变换所在的点位，就拼出了不同的图案. 在本章中，我们将学习平面直角坐标系等有关知识，由此建立图形与数量之间的联系.这将为几何问题和代数问题的相互转化打下基础.
9.1用坐标描述平面内点的位置
9.1.1平面直角坐标系的概念
1.理解平面直角坐标系以及横轴、纵轴、原点、坐标等概念，认识并能画出平面直角坐标系.2.理解各象限内及坐标轴上点的坐标特征.（重点）3.会用象限或坐标轴说明直角坐标系内点的位置，能根据横、纵坐标的符号确定点的位置．（难点）
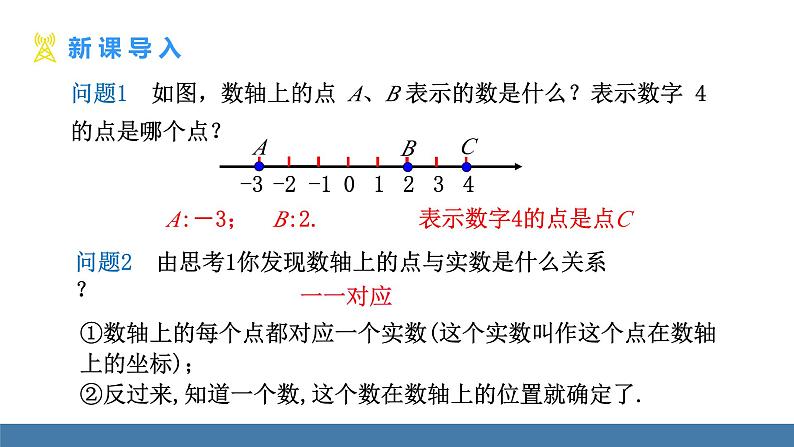
问题1 如图，数轴上的点 A、B 表示的数是什么？表示数字 4的点是哪个点？
问题2 由思考1你发现数轴上的点与实数是什么关系？
一一对应
A:－3； B:2.
①数轴上的每个点都对应一个实数(这个实数叫作这个点在数轴上的坐标)；②反过来,知道一个数,这个数在数轴上的位置就确定了.
思考 类似于利用数轴确定直线上点的位置，能不能找到一种办法来确定平面内的点的位置呢(例如下图中A,B,C,D,E各点)?
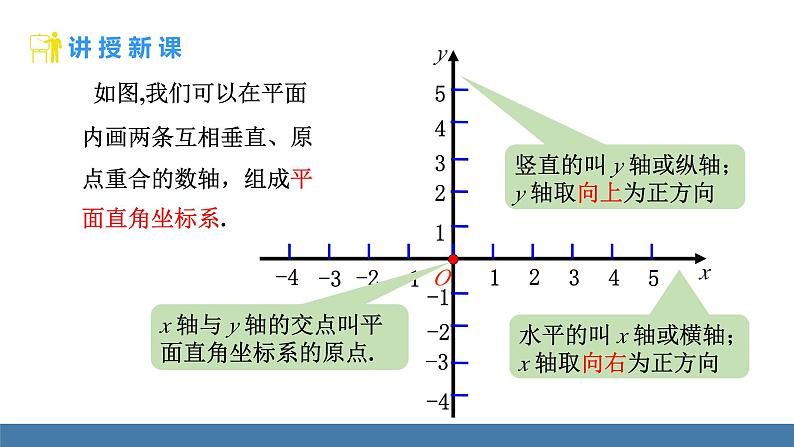
如图,我们可以在平面内画两条互相垂直、原点重合的数轴，组成平面直角坐标系.
竖直的叫 y 轴或纵轴；y 轴取向上为正方向
水平的叫 x 轴或横轴；x 轴取向右为正方向
x 轴与 y 轴的交点叫平面直角坐标系的原点.
下列四个选项中，关于平面直角坐标系的画法正确的是( )
这样 A 点的横坐标是 3,纵坐标是 4，规定把横坐标写在前，纵坐标在后，记作：A(3，4)
思考 如图点 A 如何表示呢？
后由 A 点向 y 轴画垂线，垂足 N在 y 轴上的坐标是 4.
先由 A 点向 x 轴画垂线，垂足M 在x轴上的坐标是3,
有序数对(3，4)就叫做点 A 在平面直角坐标系中的坐标，简称点 A 的坐标.
思考 原点 O 的坐标是什么？ x 轴和 y 轴上的点的坐标有什么特点？
原点 O 的坐标为(0,0)；x 轴上的点的纵坐标为 0，y 轴上的点的横坐标为 0.
请你写出点 B,C,D,E 的坐标：B(_____,_____),C(_____,_____),D(_____,_____),E(_____,_____).
例1 写出下图中的多边形 ABCDEF 各个顶点的坐标.
A（－2，0） B（0，－3） C（3，－3） D（4，0） E（3，3） F（0，3）
建立了平面直角坐标系以后，坐标平面就被两条坐标轴分成 Ⅰ，Ⅱ，Ⅲ，Ⅳ 四个部分，每个部分称为象限，分别叫做第一象限、第二象限、第三象限和第四象限.
1 2 3 4
☀注意 坐标轴上的点不属于任何一个象限.
观察坐标系，填写各象限内点的坐标的特征：
不看平面直角坐标系，你能迅速说出A(4，5)，B(－2，3)，C(－4，－1)，D(2.5，－2) 所在的象限吗？
不看平面直角坐标系，你能迅速说出A(4，0)，B(0，3)，C(－4，0)，D(0，－4)，O(0，0)所在的位置吗？
观察坐标系，填写坐标轴上的点的坐标的特征：
原点既在 x轴上，又在 y 轴上
问题 坐标平面内的点与有序数对(坐标)是什么关系?
类似数轴上的点与实数是一一对应的.我们可以得出：①对于坐标平面内任意一点 M,都有唯一的一对有序实数(x,y) (即点 M 的坐标）和它对应；②反过来，对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点 M (即坐标为(x,y)的点）和它对应.也就是说，坐标平面内的点与有序实数对是一一对应的.
例2 在平面直角坐标系中，描出下列各点，并指出它们分别在哪个象限. A(4,5)，B(－2,3)，C(－2.5,－2)，D(4,－2),E(0,－4).
解:如图，先在 x 轴上找到表示 5 的点，再在 y 轴上找出表示 4 的点，过这两个点分别作 x 轴，y 轴的垂线，垂线的交点就是点 A. 类似地，其他各点的位置如图所示.点A 在第一象限，点 B 在第二象限，点 C 在第三象限，点D 在第四象限.
例3 设点 M(a，b)为平面直角坐标系内的点．(1)当 a＞0，b＜0 时，点 M 位于第几象限？(2)当 ab＞0 时，点 M 位于第几象限？(3)当 a 为任意有理数，且 b＜0 时，点 M 位于第几象限？
解：(1)点 M 在第四象限；(2)在第一象限(a＞0，b＞0)或者在第三象限(a＜0，b＜0)；(3)在第三象限(a＜0，b＜0)或者第四象限(a＞0，b＜0)或者 y 轴负半轴上(a＝0，b＜0)．
例4 点 A(m＋3，m＋1)在 x 轴上，则 A 点的坐标为(　　)A．(0，－2) B．(2，0) C．(4，0) D．(0，－4)
解析：点 A(m＋3，m＋1)在 x 轴上，根据 x 轴上点的坐标特征知 m＋1＝0，求出 m 的值代入 m＋3 中即可．
例5 已知点 P 到 x 轴的距离为 2，到 y 轴的距离为 1.如果过点 P 作两坐标轴的垂线，垂足分别在 x 轴的正半轴上和 y 轴的负半轴上，那么点 P 的坐标是(　　)A.(2，－1) B.(1，－2) C.(－2，－1) D.(1，2)
解析：由点 P 到 x 轴的距离为 2，可知点 P 的纵坐标的绝对值为 2，又因为垂足在 y 轴的负半轴上，则纵坐标为－2；由点 P到 y 轴的距离为 1，可知点 P 的横坐标的绝对值为 1，又因为垂足在 x 轴的正半轴上，则横坐标为 1.故点 P 的坐标是(1，－2)．
1.在平面直角坐标系中，点 A(－2，3)位于哪个象限？( )A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.在平面直角坐标系的第二象限内有一点 M ，点 M 到 x 轴的距离为 3，到 y 轴的距离为 4，则点 M 的坐标是( )A. (3，－4)B. (4，－3)C. (－4，3)D. (－3，4)
3.已知点 A 的坐标为(a＋1，3－a)，下列说法正确的是( )A.若点 A 在 y 轴上，则 a＝3B.若点 A 在第一、三象限角平分线上，则 a＝1C.若点 A 到 x 轴的距离是 3，则 a＝±6D.若点 A 在第四象限，则 a 的值可以为 －2
4.如图，在平面直角坐标系中，(1) 写出 A，B，C 三点的坐标；(2) 描出点 D(2，－3)，E(－2，4)，F(0，－2).