2024-2025学年北京市房山区高三上学期期中数学检测试题

这是一份2024-2025学年北京市房山区高三上学期期中数学检测试题，共5页。试卷主要包含了 已知集合，则， 函数的零点一定位于区间， 若，且，则与的夹角是等内容，欢迎下载使用。
第Ⅰ卷 （选择题 共40分）
一．选择题 本题共10题每题4分，共计40分．在下列各题的四个选项中，只有一个选项是符合题目要求的．
1. 已知集合，则（ ）
A. B. C. D.
2. 下列函数值中，在区间上不是单调函数的是（ ）
A. B. C. D.
3. 在平面直角坐标系中，角以为始边，终边与单位圆交于点，则（ ）
A. B. C. D.
4. 已知向量在正方形网格中的位置如图所示，若网格中每个小正方形的边长均为1，则（ ）
A. B. C. D.
5. 不等式成立的一个充分不必要条件是（ ）
A. B.
C. D.
6. 函数的零点一定位于区间
A. （1, 2）B. （2, 3）C. （3, 4）D. （4, 5）
7. 若，且，则与的夹角是（ ）
A. B. C. D.
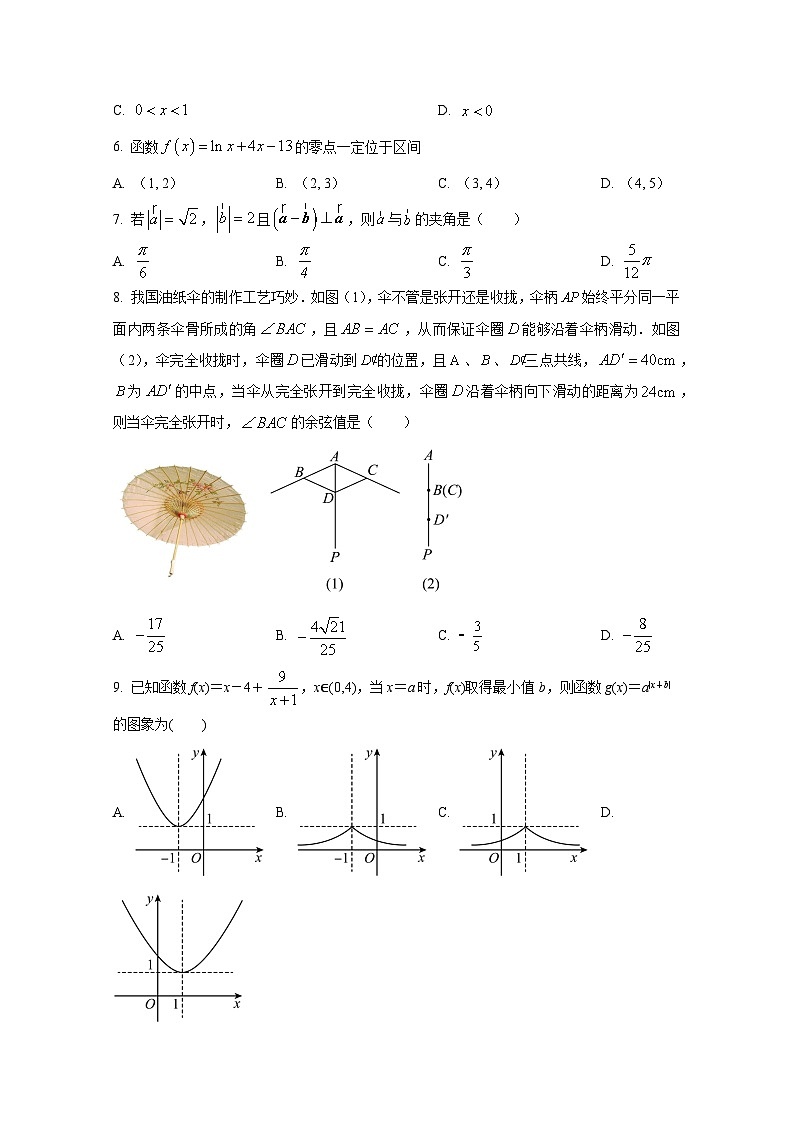
8. 我国油纸伞的制作工艺巧妙．如图（1），伞不管是张开还是收拢，伞柄始终平分同一平面内两条伞骨所成的角，且，从而保证伞圈能够沿着伞柄滑动．如图（2），伞完全收拢时，伞圈已滑动到的位置，且、、三点共线，，为的中点，当伞从完全张开到完全收拢，伞圈沿着伞柄向下滑动的距离为，则当伞完全张开时，的余弦值是（ ）

A. B. C. D.
9. 已知函数f(x)＝x－4＋，x∈(0,4)，当x＝a时，f(x)取得最小值b，则函数g(x)＝a|x＋b|的图象为( )
A. B. C. D.
10. 若，可以作为一个三角形的三条边长，则称函数是区间上的“稳定函数”.已知函数是区间上的“稳定函数”，则实数的取值范围为（ ）
A. B.
C. D.
第Ⅱ卷 （非选择题 共110分）
二．填空题（共5道小题，每题5分，共25分．把答案填在题中横线上．）
11. 函数的定义域为__________．
12 已知，则________.
13. 已知向量，.若存在实数，使得与的方向相反，则的一个取值为________.
14. 函数的最小正周期为________;若函数在区间上单调递增，则的最大值为________.
15. 已知函数，其中且．给出下列四个结论：
①若，则函数的零点是；
②若函数无最小值，则的取值范围为；
③若，则在区间上单调递减，在区间上单调递增；
④若关于的方程恰有三个不相等的实数根，则的取值范围为，且的取值范围为．
其中，所有正确结论序号是_____．
16. 已知函数．
（1）求的值
（2）求函数在区间上的最小值和最大值．
17. 已知在四棱锥中，底面是边长为4的正方形，是正三角形，平面分别是的中点．
（1）求证：平面；
（2）求平面与平面所夹角的大小；
18. 某商家为了促销，规定每位消费者均可免费参加一次抽奖活动，活动规则如下：在一不透明纸箱中有8张相同卡片，其中4张卡片上印有“幸”字，另外4张卡片上印有“运”字．消费者从该纸箱中不放回地随机抽取4张卡片，若抽到的4张卡片上都印有同一个字，则获得一张10元代金券；若抽到的4张卡片中恰有3张卡片上印有同一个字，则获得一张5元代金券；若抽到的4张卡片是其他情况，则不获得任何奖励．
（1）求某位消费者在一次抽奖活动中抽到的4张卡片上都印有“幸”字的概率；
（2）记随机变量X为某位消费者在一次抽奖活动中获得代金券金额数，求X的分布列和数学期望；
（3）该商家规定，消费者若想再次参加该项抽奖活动，则每抽奖一次需支付3元．若你是消费者，是否愿意再次参加该项抽奖活动？请说明理由．
19. 在中，．
（1）求b；
（2）在下列三个条件中选择一个作为已知，使存在且唯一确定，并求的面积．
条件①：；
条件②：边上中线的长为；
条件③：．
注：如果选择多个符合要求的条件分别解答，按第一个解答计分．
20. 已知函数．
（1）当时，求的单调区间和极值；
（2）当时，求证：；
21 已知函数．
(Ⅰ)求证：1是函数的极值点；
(Ⅱ)设是函数的导函数，求证：．