2022-2023学年广东省汕头市金平区八年级（上）期末数学试卷

这是一份2022-2023学年广东省汕头市金平区八年级（上）期末数学试卷，共5页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（3分）计算：a3•a3的值为（ ）
A．a9B．a6C．2a3D．2a6
2．（3分）若分式在实数范围内有意义，则x的取值范围是（ ）
A．x≠﹣4B．x≠0C．x≠4D．x＞﹣4
3．（3分）与分式相等的是（ ）
A．B．C．D．
4．（3分）下列分式中，是最简分式的是（ ）
A． B． C． D．
5．（3分）下列每组数分别是三根木棒的长度（单位：cm），能用它们首尾相连摆成一个三角形的是（ ）
A．3，5，8B．8，15，6C．11，5，5D．20，13，12
6．（3分）如图，图中三角形的个数共有（ ）
A．3个B．4个C．5个D．6个
7．（3分）下列图形具有稳定性的是（ ）
A．B．C．D．
8．（3分）如图，是尺规作图中“画一个角等于已知角”的示意图，该作法运用了“全等三角形的对应角相等”这一性质，则判定图中两三角形全等的条件是（ ）
A．SASB．ASAC．AASD．SSS
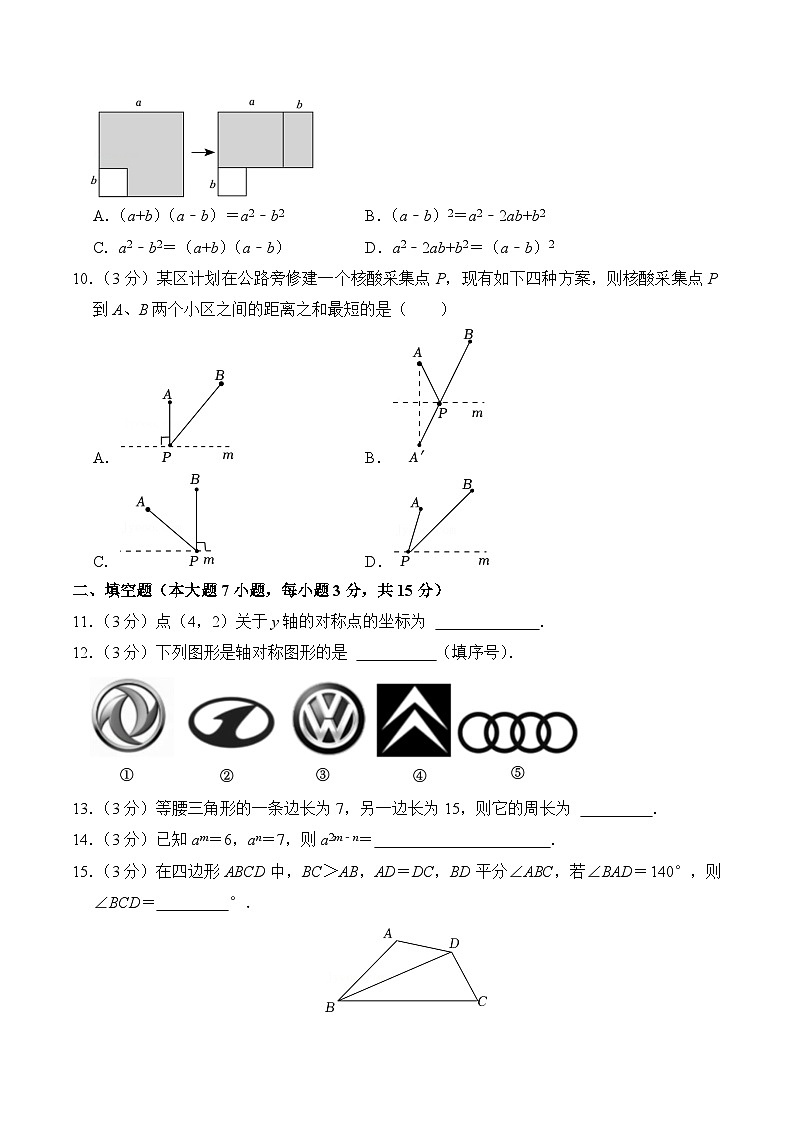
9．（3分）如图，在边长为a的正方形中挖掉一个边长为b的小正方形（a＞b），把余下的部分剪成一个长方形，通过计算两个图形（阴影部分、从左图到右图）的面积，验证的公式为（ ）
A．（a+b）（a﹣b）＝a2﹣b2B．（a﹣b）2＝a2﹣2ab+b2
C．a2﹣b2＝（a+b）（a﹣b）D．a2﹣2ab+b2＝（a﹣b）2
10．（3分）某区计划在公路旁修建一个核酸采集点P，现有如下四种方案，则核酸采集点P到A、B两个小区之间的距离之和最短的是（ ）
A．B．
C．D．
二、填空题（本大题7小题，每小题3分，共15分）
11．（3分）点（4，2）关于y轴的对称点的坐标为 ．
12．（3分）下列图形是轴对称图形的是 （填序号）．
13．（3分）等腰三角形的一条边长为7，另一边长为15，则它的周长为 ．
14．（3分）已知am＝6，an＝7，则a2m﹣n＝ ．
15．（3分）在四边形ABCD中，BC＞AB，AD＝DC，BD平分∠ABC，若∠BAD＝140°，则∠BCD＝ °．
三、解答题（一）（本大题共3小题，每小题8分，共24分）
16．（8分）化简：（x+y）（x﹣y）﹣（x+y）2
17．（8分）先化简，再求值：（﹣1）÷，其中a＝﹣2．
18．（8分）如图，在△ABC中，点D在边BC上，CD＝AB，DE∥AB，∠DCE＝∠A．求证：DE＝BC．
四、解答题（二）（本大题共3小题，每小题9分，共27分）
19．（9分）如图，在△ABC中，∠B＝42°，∠C＝68°，点E为线段AB的中点，点F在边AC上，连接EF，沿EF将△AEF折叠得到△PEF．
（1）如图①，当点P落在BC上时，求∠AEP的度数；
（2）如图②，当PF⊥AC时，求∠BEP的度数．
20．（9分）仙桃是遂宁市某地的特色时令水果．仙桃一上市，水果店的老板用2400元购进一批仙桃，很快售完；老板又用3750元购进第二批仙桃，所购件数是第一批的倍，但进价比第一批每件多了5元．
（1）第一批仙桃每件进价是多少元？
（2）老板以每件225元的价格销售第二批仙桃，售出80%后，为了尽快售完，剩下的决定打折促销．要使得第二批仙桃的销售利润不少于2460元，剩余的仙桃每件售价最多打几折？（利润＝售价﹣进价）
21．（9分）若a＞0，，．
（1）当a＝5时，计算M、N的值；
（2）猜想M与N的大小关系，并证明你的猜想．
五、解答题（三）（本大题共2小题，每小题12分，共24分）
22．（12分）（1）阅读理解：如图1，在△ABC中，若AB＝3，AC＝5．求BC边上的中线AD的取值范围，小聪同学是这样思考的：延长AD至E，使DE＝AD，连接BE．利用全等将边AC转化到BE，在△BAE中利用三角形三边关系即可求出中线AD的取值范围，在这个过程中小聪同学证三角形全等用到的判定方法是 ，中线AD的取值范围是 ；
（2）问题解决：如图2，在△ABC中，点D是BC的中点，DM⊥DN．DM交AB于点M，DN交AC于点N．求证：BM+CN＞MN；
（3）问题拓展：如图3，在△ABC中，点D是BC的中点，分别以AB，AC为直角边向△ABC外作Rt△ABM和Rt△ACN，其中∠BAM＝∠NAC＝90°，AB＝AM，AC＝AN，连接MN，请你探索AD与MN的数量与位置关系，并直接写出AD与MN的关系．
23．（12分）如图，在平面直角坐标系中，点A、B、C在坐标轴上，且△ABC为等边三角形，E为线段OC上一动点，如图，在x轴下方作AP＝AE，且∠EAP＝60°，连接OP，BP．
（1）求证：△ACE≌△ABP；
（2）若点C坐标为，求当OE等于多少时，点P在y轴上；
（3）若点A坐标为（﹣3，0），请直接写出在点E运动的过程中，OP的最小值．