第22课时 多边形与平行四边形-【备战中考】2025年中考数学一轮总复习课件

这是一份第22课时 多边形与平行四边形-【备战中考】2025年中考数学一轮总复习课件，共30页。PPT课件主要包含了n－2·180°，n－3，轴对称，知识点2平行四边形，两组对边分别平行，互相平分，两条对角线的交点，答案图1，答案图2等内容，欢迎下载使用。
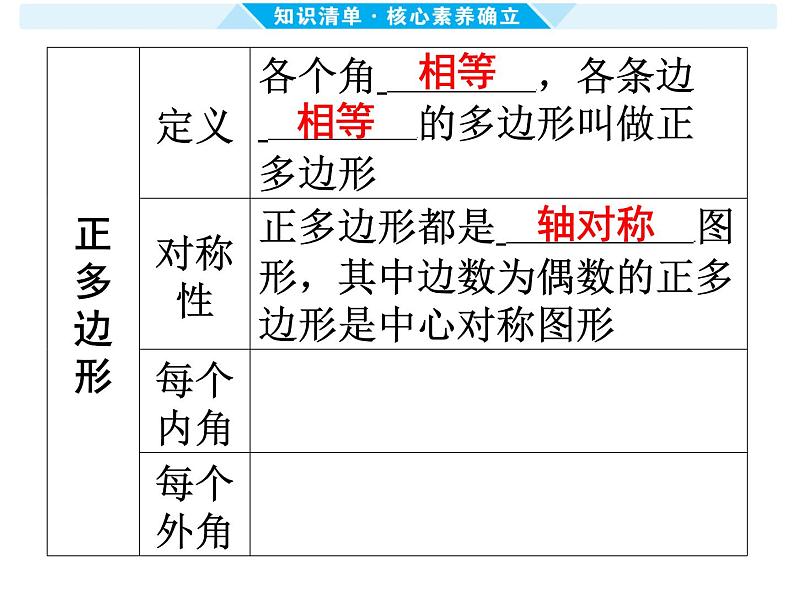
知识点1 多边形的有关概念和性质
两条对角线的交点
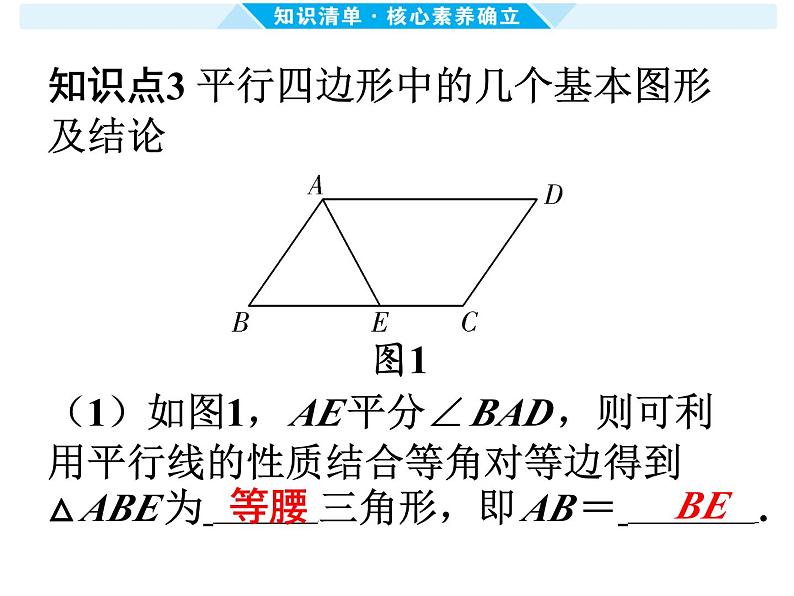
知识点3 平行四边形中的几个基本图形 及结论
（1）如图1，AE平分∠BAD，则可利 用平行线的性质结合等角对等边得到 △ABE为 三角形，即AB＝ ⁠.
（2）如图2，平行四边形的一条对角线 把其分为两个全等的三角形，如 △ABD≌△CDB（△ABC≌△CDA）；两条对角线把平行四边形分为两组全等的三角形，如△AOD≌△COB，△AOB≌△COD；根据平行四边形的中心对称性，可得经过对称中心O的线段与对角线所组成的居于中心对称位置的三角形全等，如△AOE≌△COF. 图2中阴影部分的面积为平行四边形面积的 ⁠.
（4）如图4，根据平行四边形的面积的 求法，可得AE·BC＝AF·CD.

图3 图4
名师指津1. 多边形的有关证明和计算，经常转化 为三角形的有关证明和计算，体现数学 的化归思想.2. 若一条直线过平行四边形的对角线的 交点，则这条直线被一组对边截下的线 段以对角线的交点为对称中心，且这条 直线等分平行四边形的面积.3. 判定平行四边形的基本思路：
（1）若已知一组对边平行，可以证明这 一组对边相等，或另一组对边平行；（2）若已知一组对边相等，可以证明这 一组对边平行，或另一组对边相等；（3）若已知条件与对角线相关，可考虑 证明对角线互相平分；（4）若已知一组对角相等，可以证明另 一组对角相等.
考点一　多边形的有关概念及性质
例1　（1）下列说法错误的是（　C　）
（2）若一个多边形的内角和比外角和大 360°，则这个多边形的边数为 ⁠；
（3）（2024·威海）如图，在正六边形 ABCDEF中，AH∥FG，BI⊥AH，垂 足为I. 若∠EFG＝20°，则∠ABI＝ ⁠.
考点二　平行四边形的判定例2　 如图，在四边形ABCD中，E是 AB边的中点，连接DE并延长交CB的延 长线于点F，且CB＝BF. 若添加一个条 件使四边形ABCD是平行四边形，则下 面四个条件中可选择的是（　D　）
例3　 （2024·湖南）如图，在四边形 ABCD中，AB∥CD，点E在边AB 上， 　　.请从“①∠B＝∠AED；②AE ＝BE，AE＝CD”这两组条件中任选一 组作为已知条件，填在横线上（填序 号），再解决下列问题：
[答案]解：（1）证明：选择①.∵∠B＝∠AED，∴DE∥CB. ∵AB∥CD，∴四边形BCDE为平行四边形.选择②.∵AE＝BE，AE＝CD，∴CD＝BE. ∵AB∥CD，∴四边形BCDE为平行四边形.
（1）求证：四边形BCDE为平行四边形；
（2）若AD⊥AB，AD＝8，BC＝10， 求线段AE的长.
考点三　平行四边形的性质
例4　 （1）（2024·贵州）如图1， ▱ABCD的对角线AC与BD相交于点 O，则下列结论一定正确的是（　B　）
（2）（2024·巴中）如图2，▱ABCD的 对角线AC，BD相交于点O，点E是BC 的中点，AC＝4.若▱ABCD的周长为 12，则△COE的周长为（　B　）
例5　 如图，在平行四边形ABCD中， O是对角线AC的中点，过点O作 OE⊥BC于点E，过点O作FG⊥AB分 别交AB，CD于点F，G.
（1）若BC＝5，OE＝3，求平行四边形ABCD的面积；
[答案]解：（2）证明：如答案图2，过点E作EH⊥EG，与GC的延长线交于点H. ∵OE⊥BC，EH⊥EG，∴∠OEG＋∠GEC＝∠GEC＋∠CEH＝90°，∴∠OEG＝∠CEH. ∵∠ACB＝45°，∴∠COE＝45°， ∴OE＝CE.
在平行四边形ABCD中，AB∥CD，且 FG⊥AB，∴FG⊥CD，∴∠EOG＋∠ECG＝360°－90°－ 90°＝180°.又∵∠ECH＋∠ECG＝180°， ∴∠EOG＝∠ECH，∴△OEG≌△CEH（ASA），∴OG＝CH，EG＝EH.
1. （2024·云南）一个七边形的内角和等 于（　B　）
2. （2024·长春）在剪纸活动中，小花同 学想用一张矩形纸片剪出一个正五边形，其中正五边形的一条边与矩形的边重合，如图所示，则∠α的大小为（　D　）