中考数学二轮复习几何模拟专项讲练模型10 三角形——双角平分线模型（2份，原卷版+解析版）

这是一份中考数学二轮复习几何模拟专项讲练模型10 三角形——双角平分线模型（2份，原卷版+解析版），文件包含中考数学二轮复习几何模拟专项讲练模型10三角形双角平分线模型-原卷版doc、中考数学二轮复习几何模拟专项讲练模型10三角形双角平分线模型-解析版doc等2份试卷配套教学资源，其中试卷共22页， 欢迎下载使用。

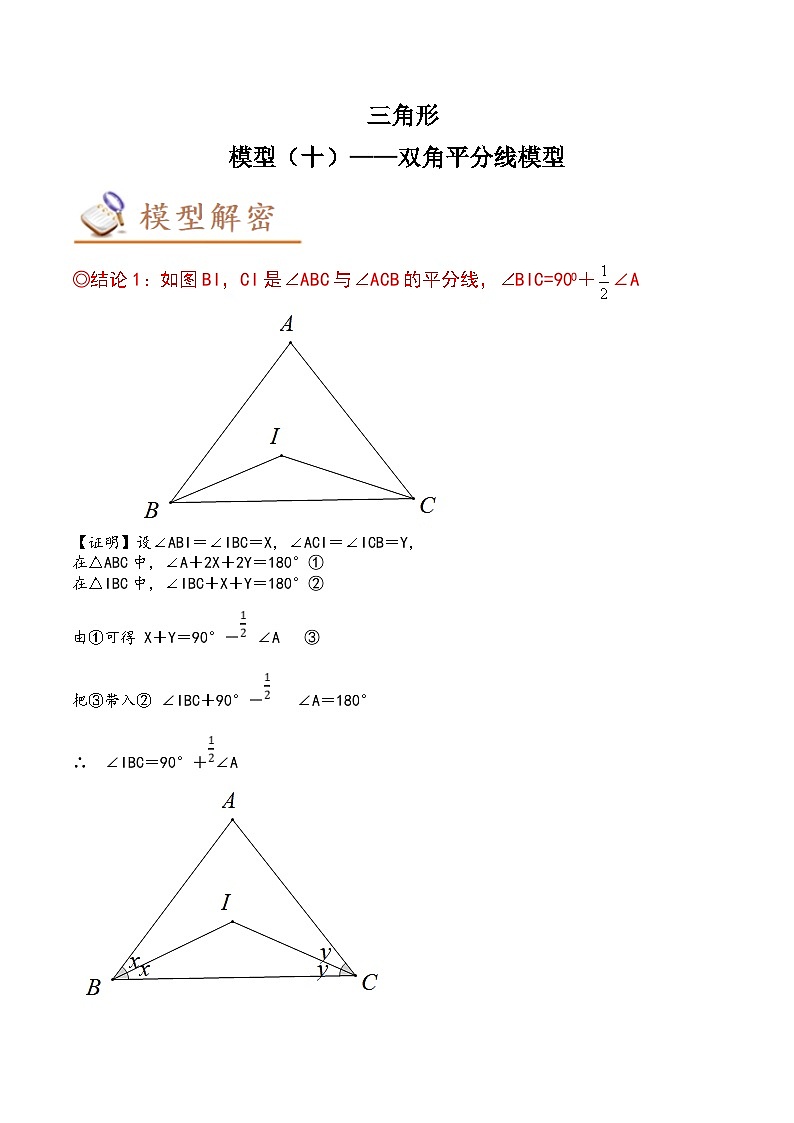
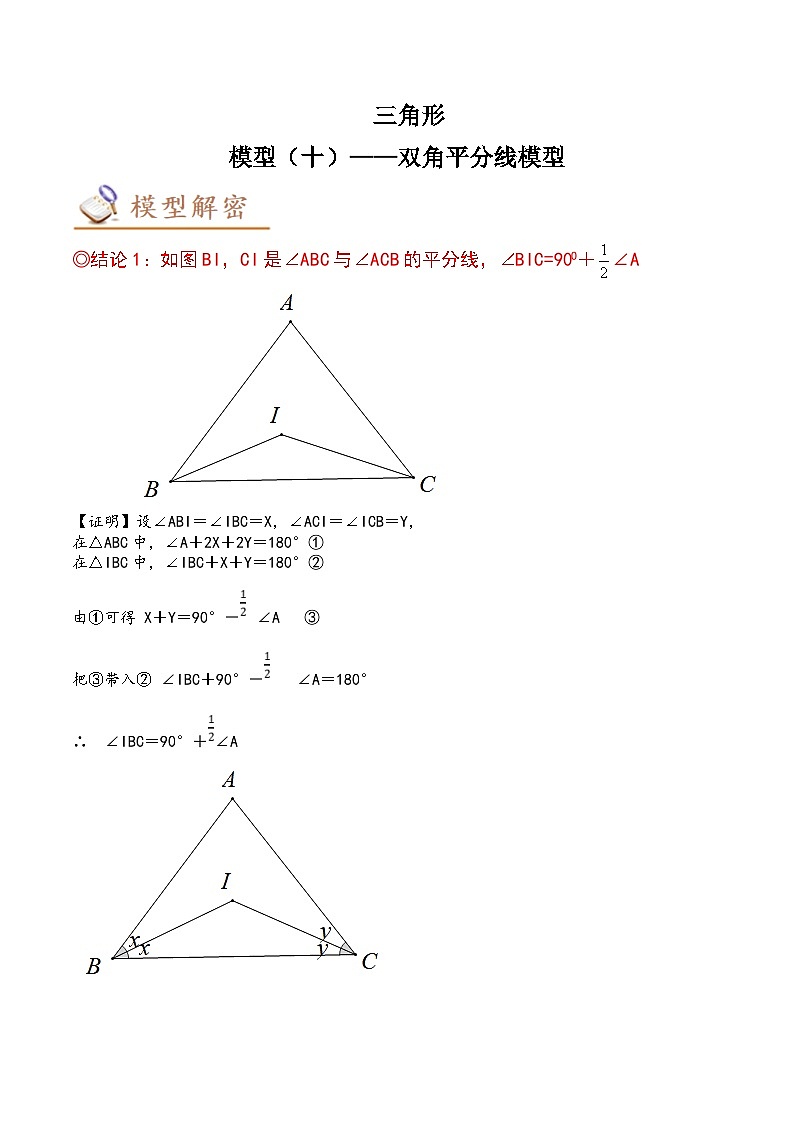
◎结论1：如图BI，CI是∠ABC与∠ACB的平分线，∠BIC=90O＋∠A

【证明】设∠ABI＝∠IBC＝X，∠ACI＝∠ICB＝Y，
在△ABC中，∠A＋2X＋2Y＝180°①
在△IBC中，∠IBC＋X＋Y＝180°②
由①可得 X＋Y＝90°－∠A ③
把③带入② ∠IBC＋90°－∠A＝180°
∴ ∠IBC＝90°＋∠A
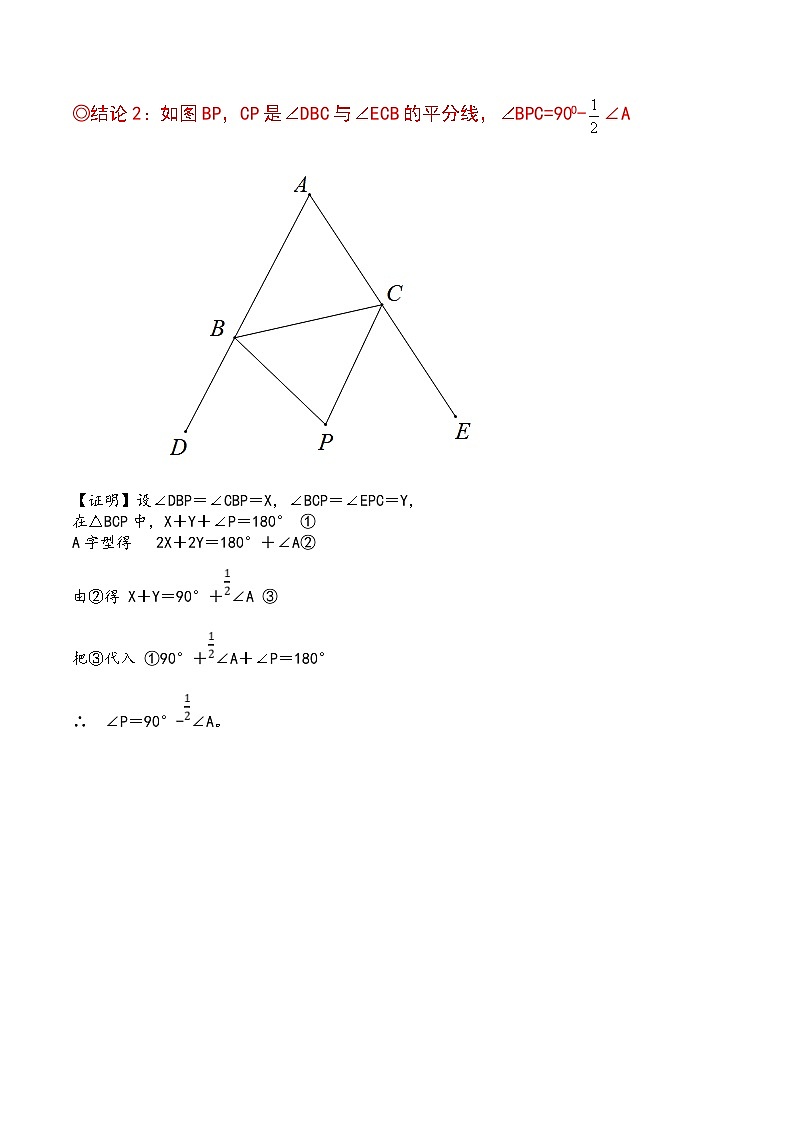
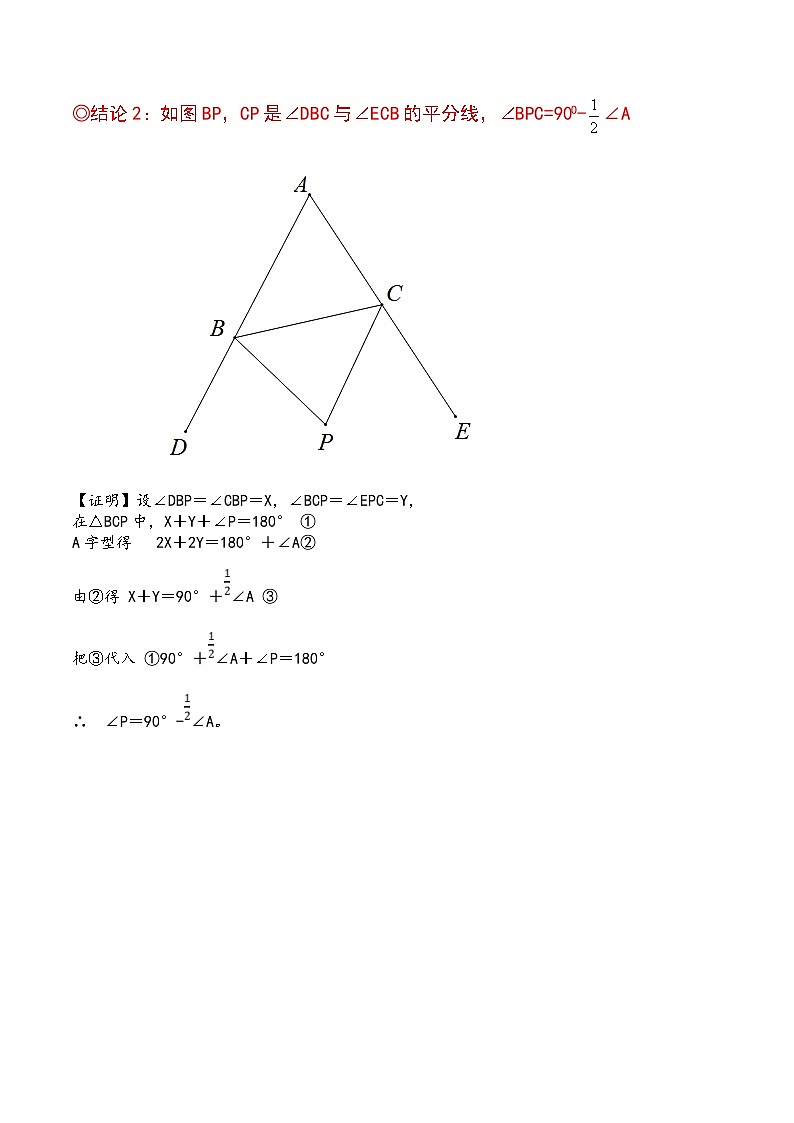
◎结论2：如图BP，CP是∠DBC与∠ECB的平分线，∠BPC=90O-∠A

【证明】设∠DBP＝∠CBP＝X，∠BCP＝∠EPC＝Y，
在△BCP中，X＋Y＋∠P＝180° ①
A字型得 2X＋2Y＝180°＋∠A②
由②得 X＋Y＝90°＋∠A ③
把③代入 ①90°＋∠A＋∠P＝180°
∴ ∠P＝90°-∠A。
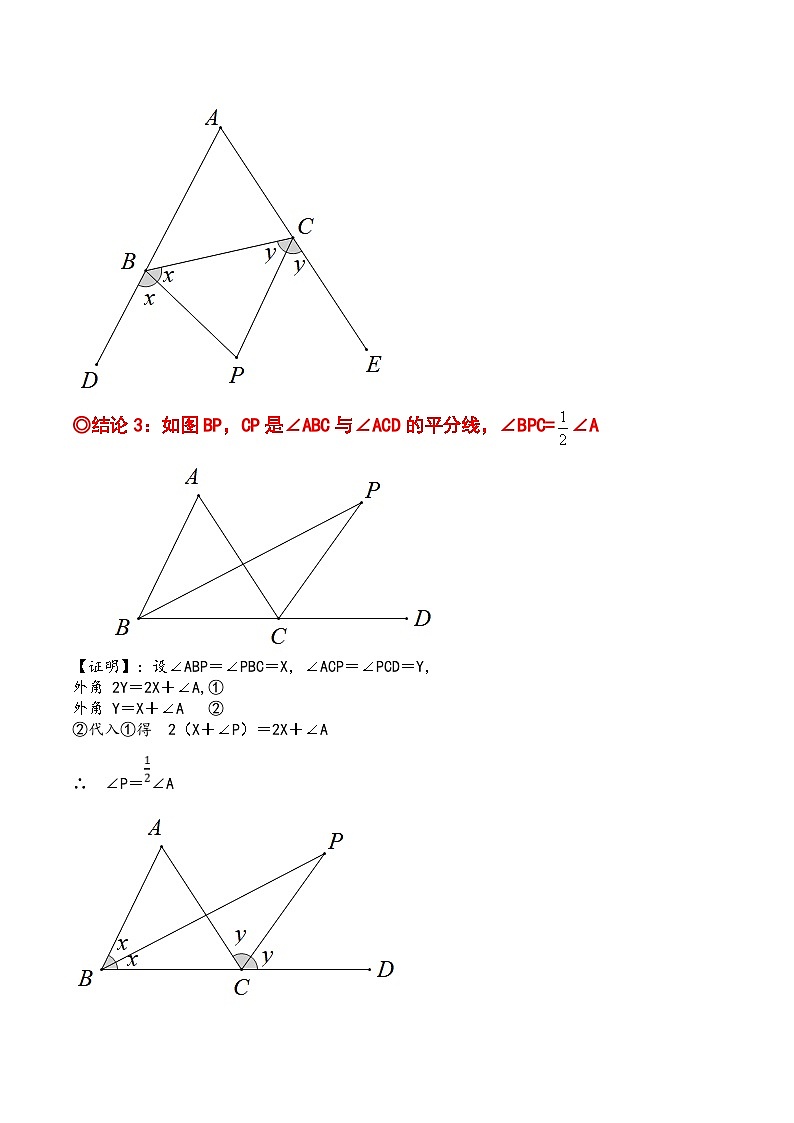
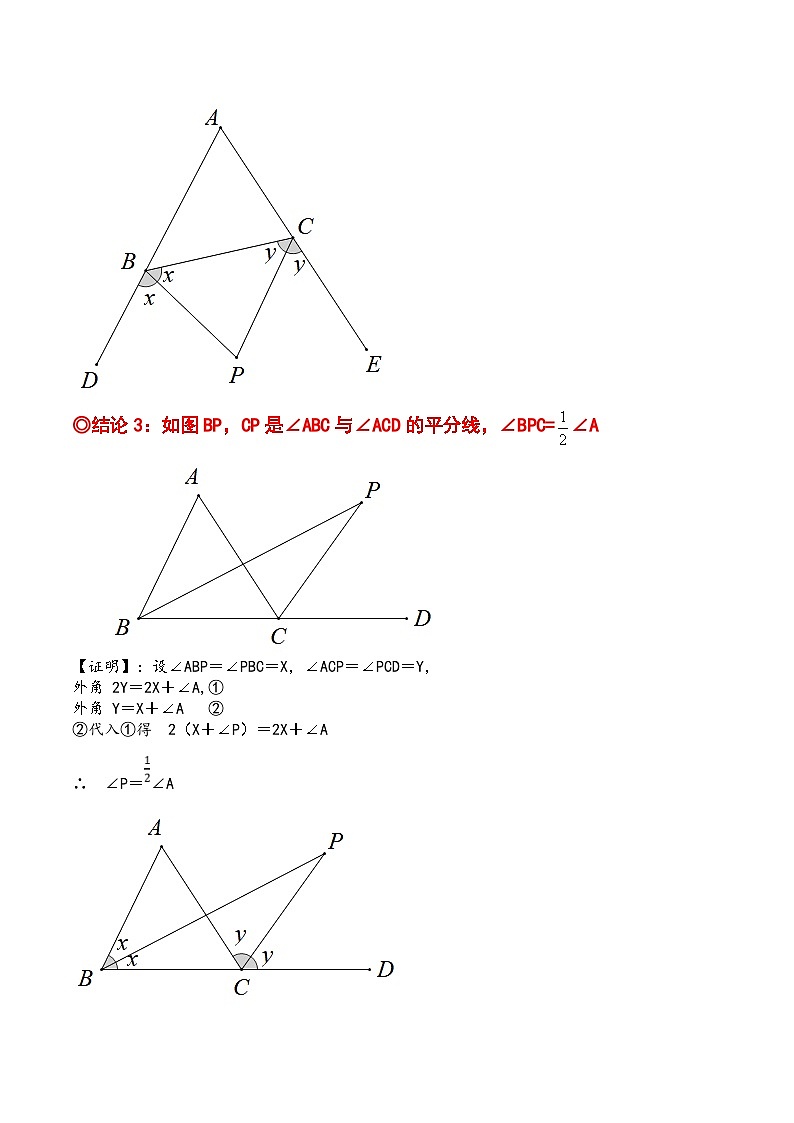
◎结论3：如图BP，CP是∠ABC与∠ACD的平分线，∠BPC=∠A

【证明】：设∠ABP＝∠PBC＝X，∠ACP＝∠PCD＝Y，
外角 2Y＝2X＋∠A,①
外角 Y＝X＋∠A ②
②代入①得 2（X＋∠P）＝2X＋∠A
∴ ∠P＝∠A
注：双角平分线模型不仅可以帮助同学们秒杀选填问题，而且在复杂约几何解答题中也能快速理清角度之间的关系，进而解决问题﹒
1．（2021·全国·九年级专题练习）如图所示，在中，的平分线相交于点F，若且∠ABC=42°，，则等于（ ）．
A．B．C．D．
2．（2022·全国·八年级课时练习）如图，△ABC中，∠E=18°，BE平分∠ABC，CE平分∠ACD，则∠A等于（ ）
A．36°B．30°C．20°D．18°
3．（2015·广西钦州·八年级期中）如图，在△ABC中，∠ABC和∠ACB的外角平分线交于点O，设∠A=m，则∠BOC =（ ）
A．B．C．D．

1．（2022·全国·八年级课时练习）如图，BA1和CA1分别是△ABC的内角平分线和外角平分线，BA2是∠A1BD的角平分线CA2是∠A1CD的角平分线，BA3是A2BD∠的角平分线，CA3是∠A2CD的角平分线，若∠A1=α，则∠A2013为（ ）
A．B．C．D．
2．（2022·全国·八年级课时练习）如图，在△ABC中，∠ABC和∠ACB的角平分线交于点O，延长BO与∠ACB的外角平分线交于点D，若∠BOC＝130°，则∠D＝_____
3．（2022·江苏·宜兴市和桥镇第二中学七年级阶段练习）如图在△ABC中，BO，CO分别平分∠ABC，∠ACB，交于O，CE为外角∠ACD的平分线，交BO的延长线于点E，记，，则以下结论①，②，③，④，正确的是________．（把所有正确的结论的序号写在横线上）
1．（2022·广东·深圳市宝安中学（集团）三模）如图，在△ABC中，，△ABC的两条角平分线BF、CE相交于点G．
(1) 度．
(2)如图，平行四边形ABCD中，对角线，在AD上截取AH＝AB，连接BH交AC于点F，过点C作CE平分交BH于点G．若，．
①求的值．
②求．
2．（2022·山东·济南育英中学模拟预测）如图1，在△ABC中，∠BAC的平分线AD与∠BCA的平分线CE交于点O．
(1)求证：∠AOC＝90°＋∠ABC；
(2)当∠ABC＝90°时，且AO＝3OD（如图2），判断线段AE，CD，AC之间的数量关系，并加以证明．