2024年中考数学几何模型专项复习讲与练 模型10 三角形——双角平分线模型-原卷版+解析

这是一份2024年中考数学几何模型专项复习讲与练 模型10 三角形——双角平分线模型-原卷版+解析，共19页。


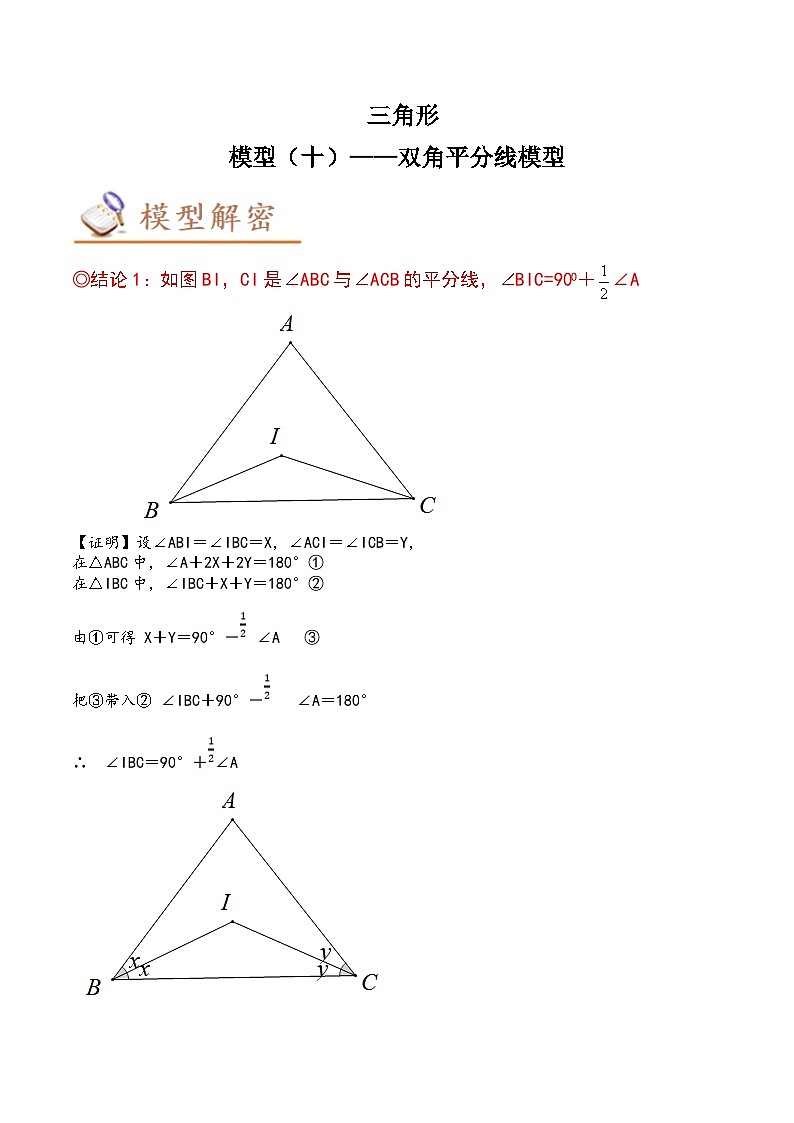
◎结论1：如图BI，CI是∠ABC与∠ACB的平分线，∠BIC=90O＋∠A

【证明】设∠ABI＝∠IBC＝X，∠ACI＝∠ICB＝Y，
在△ABC中，∠A＋2X＋2Y＝180°①
在△IBC中，∠IBC＋X＋Y＝180°②
由①可得 X＋Y＝90°－∠A ③
把③带入② ∠IBC＋90°－∠A＝180°
∴ ∠IBC＝90°＋∠A
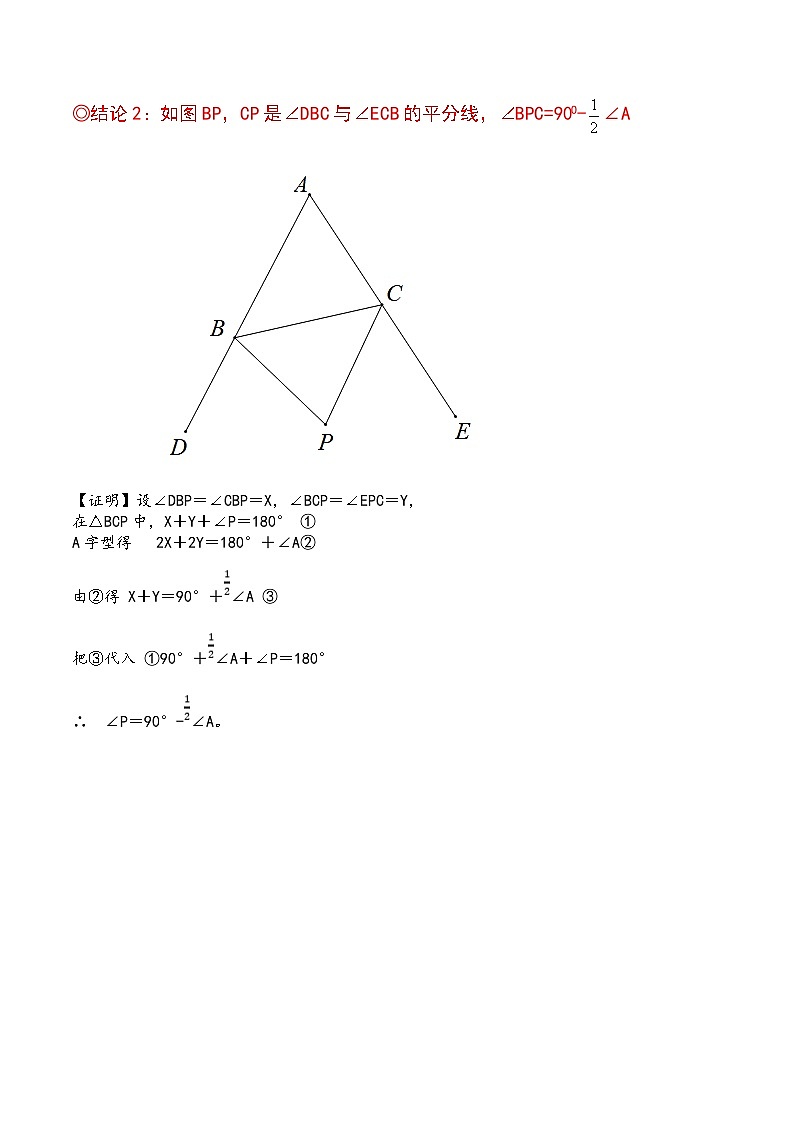
◎结论2：如图BP，CP是∠DBC与∠ECB的平分线，∠BPC=90O-∠A

【证明】设∠DBP＝∠CBP＝X，∠BCP＝∠EPC＝Y，
在△BCP中，X＋Y＋∠P＝180° ①
A字型得 2X＋2Y＝180°＋∠A②
由②得 X＋Y＝90°＋∠A ③
把③代入 ①90°＋∠A＋∠P＝180°
∴ ∠P＝90°-∠A。
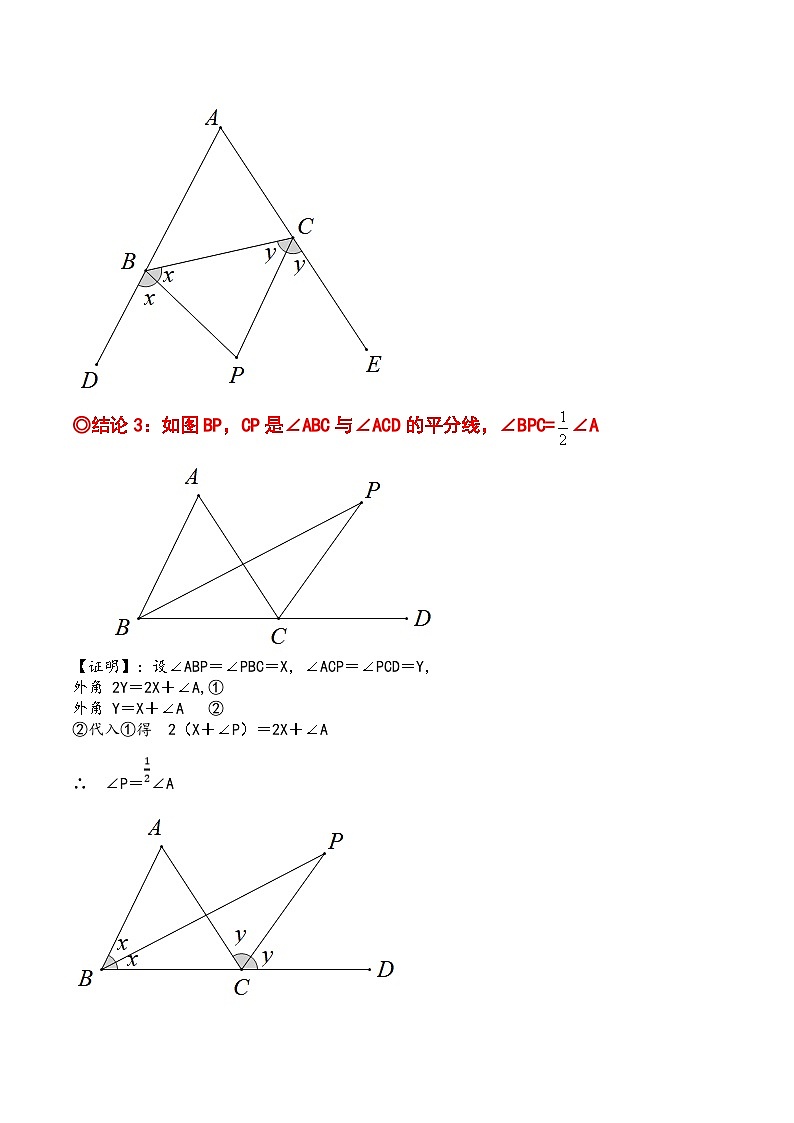
◎结论3：如图BP，CP是∠ABC与∠ACD的平分线，∠BPC=∠A

【证明】：设∠ABP＝∠PBC＝X，∠ACP＝∠PCD＝Y，
外角 2Y＝2X＋∠A,①
外角 Y＝X＋∠A ②
②代入①得 2（X＋∠P）＝2X＋∠A
∴ ∠P＝∠A
注：双角平分线模型不仅可以帮助同学们秒杀选填问题，而且在复杂约几何解答题中也能快速理清角度之间的关系，进而解决问题﹒
1． (2023·全国·九年级专题练习）如图所示，在中，的平分线相交于点F，若且∠ABC=42°，，则等于（ ）．
A．B．C．D．
2． (2023·全国·八年级课时练习）如图，△ABC中，∠E=18°，BE平分∠ABC，CE平分∠ACD，则∠A等于（ ）
A．36°B．30°C．20°D．18°
3．（2015·广西钦州·八年级期中）如图，在△ABC中，∠ABC和∠ACB的外角平分线交于点O，设∠A=m，则∠BOC =（ ）
A．B．C．D．

1． (2023·全国·八年级课时练习）如图，BA1和CA1分别是△ABC的内角平分线和外角平分线，BA2是∠A1BD的角平分线CA2是∠A1CD的角平分线，BA3是A2BD∠的角平分线，CA3是∠A2CD的角平分线，若∠A1=α，则∠A2013为（ ）
A．B．C．D．
2． (2023·全国·八年级课时练习）如图，在△ABC中，∠ABC和∠ACB的角平分线交于点O，延长BO与∠ACB的外角平分线交于点D，若∠BOC＝130°，则∠D＝_____
3． (2023·江苏·宜兴市和桥镇第二中学七年级阶段练习）如图在△ABC中，BO，CO分别平分∠ABC，∠ACB，交于O，CE为外角∠ACD的平分线，交BO的延长线于点E，记，，则以下结论①，②，③，④，正确的是________．（把所有正确的结论的序号写在横线上）
1． (2023·广东·深圳市宝安中学（集团）三模）如图，在△ABC中，，△ABC的两条角平分线BF、CE相交于点G．
(1) 度．
(2)如图，平行四边形ABCD中，对角线，在AD上截取AH＝AB，连接BH交AC于点F，过点C作CE平分交BH于点G．若，．
①求的值．
②求．
2． (2023·山东·济南育英中学模拟预测）如图1，在△ABC中，∠BAC的平分线AD与∠BCA的平分线CE交于点O．
(1)求证：∠AOC＝90°＋∠ABC；
(2)当∠ABC＝90°时，且AO＝3OD（如图2），判断线段AE，CD，AC之间的数量关系，并加以证明．
三角形
模型（十）——双角平分线模型
◎结论1：如图BI，CI是∠ABC与∠ACB的平分线，∠BIC=90O＋∠A

【证明】设∠ABI＝∠IBC＝X，∠ACI＝∠ICB＝Y，
在△ABC中，∠A＋2X＋2Y＝180°①
在△IBC中，∠IBC＋X＋Y＝180°②
由①可得 X＋Y＝90°－∠A ③
把③带入② ∠IBC＋90°－∠A＝180°
∴ ∠IBC＝90°＋∠A
◎结论2：如图BP，CP是∠DBC与∠ECB的平分线，∠BPC=90O-∠A

【证明】设∠DBP＝∠CBP＝X，∠BCP＝∠EPC＝Y，
在△BCP中，X＋Y＋∠P＝180° ①
A字型得 2X＋2Y＝180°＋∠A②
由②得 X＋Y＝90°＋∠A ③
把③代入 ①90°＋∠A＋∠P＝180°
∴ ∠P＝90°-∠A。
◎结论3：如图BP，CP是∠ABC与∠ACD的平分线，∠BPC=∠A

【证明】：设∠ABP＝∠PBC＝X，∠ACP＝∠PCD＝Y，
外角 2Y＝2X＋∠A,①
外角 Y＝X＋∠A ②
②代入①得 2（X＋∠P）＝2X＋∠A
∴ ∠P＝∠A
注：双角平分线模型不仅可以帮助同学们秒杀选填问题，而且在复杂约几何解答题中也能快速理清角度之间的关系，进而解决问题﹒
1． (2023·全国·九年级专题练习）如图所示，在中，的平分线相交于点F，若且∠ABC=42°，，则等于（ ）．
A．B．C．D．
【答案】B
【分析】由∠ABC=42°，∠A=60°，根据三角形内角和等于180°，可得∠ACB的度数，又因为∠ABC、∠ACB的平分线分别为BE、CD，所以可以求得∠FBC和∠FCB的度数，从而求得∠BFC的度数．
【详解】解：∵．
∴
又∵∠ABC、∠ACB的平分线分别为BE、CD．
∴，
又∵．
∴．
故选：B．
【点睛】本题考查三角形内角和和角平分线的相关知识，关键是可以根据题目中的信息，灵活变化求出相应问题的答案．
2． (2023·全国·八年级课时练习）如图，△ABC中，∠E=18°，BE平分∠ABC，CE平分∠ACD，则∠A等于（ ）
A．36°B．30°C．20°D．18°
【答案】A
【分析】由三角形的一个外角等于与它不相邻的两个内角的和，得∠ACD=∠A+∠ABC，∠ECD=∠E+∠EBC；由角平分线的性质，得∠ECD=（∠A+∠ABC），∠EBC=∠ABC，利用等量代换，即可求得∠A与∠E的关系，即可得到结论．
【详解】解：∵∠ACD=∠A+∠ABC，
∴∠ECD=（∠A+∠ABC）．
又∵∠ECD=∠E+∠EBC，
∴∠E+∠EBC=（∠A+∠ABC）．
∵BE平分∠ABC，
∴∠EBC=∠ABC，
∴∠ABC+∠E=（∠A+∠ABC），
∴∠E=∠A=18°，
∴∠A=36°．
故选A．
3．（2015·广西钦州·八年级期中）如图，在△ABC中，∠ABC和∠ACB的外角平分线交于点O，设∠A=m，则∠BOC =（ ）
A．B．C．D．
【答案】B
【分析】根据三角形的内角和，可得∠ABC+∠ACB，根据角的和差，可得∠DBC+∠BCE，根据角平分线的定义，可得∠OBC+∠OCB，根据三角形的内角和，可得答案．
【详解】解：如图：
，
由三角形内角和定理，得∠ABC+∠ACB=180°-∠A=180°-m，
由角的和差，得∠DBC+∠BCE=360°-（∠ABC+∠ACB）=180°+m，
由∠ABC和∠ACB的外角平分线交于点O，得
∠OBC+∠OCB=（∠DBC+∠BCE）=90°+m，
由三角形的内角和，得
∠O=180°-（∠OBC+∠OCB）=90°-m．
故选：B．
【点睛】本题考查了三角形内角和定理，利用三角形内角和定理，角的和差，角平分线的定义是解题关键．

1． (2023·全国·八年级课时练习）如图，BA1和CA1分别是△ABC的内角平分线和外角平分线，BA2是∠A1BD的角平分线CA2是∠A1CD的角平分线，BA3是A2BD∠的角平分线，CA3是∠A2CD的角平分线，若∠A1=α，则∠A2013为（ ）
A．B．C．D．
【答案】D
【详解】∵BA1和CA1分别是△ABC的内角平分线和外角平分线，
∴∠A1BC=∠ABC，∠A1CD=∠ACD，
又∵∠ACD=∠A+∠ABC，∠A1CD=∠A1BC+∠A1，
∴∠A1BC+∠A1=(∠A+∠ABC)=∠A+∠ABC=∠A+∠A1BC，
∴∠A1=∠A；,
同理可得：∠A2=∠A1=，∠A3=∠A2=，，∠An=∠An-1=，
∴∠A2013=.
故选D．
点睛：利用三角形外角的性质和三角形内角和定理结合角平分线的定义推导得到∠A1和∠A的关系是解这道题的关键，由此可推导出∠A2与∠A1的关系，进一步推广到∠An和∠An-1的关系就可找到规律求得∠A2013.
2． (2023·全国·八年级课时练习）如图，在△ABC中，∠ABC和∠ACB的角平分线交于点O，延长BO与∠ACB的外角平分线交于点D，若∠BOC＝130°，则∠D＝_____
【答案】40°
【分析】根据角平分线的定义结合三角形外角的性质即可得到结论．
【详解】解：∵∠ABC和∠ACB的角平分线交于点O，
∴∠ACO=∠ACB，
∵CD平分∠ACE，
∴∠ACD=∠ACE，
∵∠ACB+∠ACE=180°，
∴∠OCD=∠ACO+∠ACD=（∠ACB+∠ACE）=×180°=90°，
∵∠BOC＝130°，
∴∠D=∠BOC-∠OCD=130°-90°=40°，
故答案为：40°．
【点睛】本题考查了三角形的外角性质，角平分线的定义，熟练掌握相关性质和概念正确推理计算是解题的关键．
3． (2023·江苏·宜兴市和桥镇第二中学七年级阶段练习）如图在△ABC中，BO，CO分别平分∠ABC，∠ACB，交于O，CE为外角∠ACD的平分线，交BO的延长线于点E，记，，则以下结论①，②，③，④，正确的是________．（把所有正确的结论的序号写在横线上）
【答案】①④
【分析】依据角平分线的性质以及三角形外角性质，即可得到∠1＝2∠2，∠BOC＝90°＋∠1，∠BOC＝90°＋∠2，再分析判断．
【详解】∵CE为外角∠ACD的平分线，BE平分∠ABC，
∴∠DCE＝∠ACD，∠DBE＝∠ABC，
又∵∠DCE是△BCE的外角，
∴∠2＝∠DCE−∠DBE＝（∠ACD−∠ABC）＝∠1，
故①正确；
∵BO，CO分别平分∠ABC，∠ACB，
∴∠OBC＝ABC，∠OCB＝∠ACB，
∴∠BOC＝180°−（∠OBC＋∠OCB）
＝180°−（∠ABC＋∠ACB）
＝180°−（180°−∠1）
＝90°＋∠1，
故②、③错误；
∵OC平分∠ACB，CE平分∠ACD，
∴∠ACO＝∠ACB，∠ACE＝∠ACD，
∴∠OCE＝（∠ACB＋∠ACD）＝×180°＝90°，
∵∠BOC是△COE的外角，
∴∠BOC＝∠OCE＋∠2＝90°＋∠2，故④正确；
故答案为：①④．
【点睛】本题考查了三角形的内角和定理，三角形的一个外角等于与它不相邻的两个内角的和的性质，以及角平分线的定义．
1． (2023·广东·深圳市宝安中学（集团）三模）如图，在△ABC中，，△ABC的两条角平分线BF、CE相交于点G．
(1) 度．
(2)如图，平行四边形ABCD中，对角线，在AD上截取AH＝AB，连接BH交AC于点F，过点C作CE平分交BH于点G．若，．
①求的值．
②求．
【答案】(1)；
(2)①4 ；②24．
【分析】（1）由得到，再根据角平分线的定义可知，从而得到；
（2）①连接AG，过G作，过C点作，由（1）可知是等腰直角三角形，从而得出，，，再利用∽得出，再利用也是等腰直角三角形得出，从而得出，利用∽得到，从而得到；
②利用得出，从而求出AB，最后用求面积即可．
（1）
解：
△ABC的两条角平分线BF、CE相交于点G．
故答案为：
（2）
①如图，连接AG，过G作，过C点作，
为角平分线
CE平分，为角平分线，，
∴由（1）得：，
，
∴是等腰直角三角形．
又，
．
，
，
．
∵，，
∴∽，
，即，
．
为角平分线，为角平分线，
∴AG为角平分线，（三角形的三条角平分线交于一点），
，是等腰直角三角形，
，
，
．
∵ADBC，
∽，
，即，
．
②由（2）①得， ．
∵，
∴，
，
．
【点睛】本题考查与角平分线有关的三角形内角和问题，相似三角形的判定与性质，勾股定理，等腰直角三角形的判定与性质，三角形的面积公式，三角形的三条角平分线交于一点等知识，难度较大，正确作出辅助线，掌握相关定理是解题的关键．
2． (2023·山东·济南育英中学模拟预测）如图1，在△ABC中，∠BAC的平分线AD与∠BCA的平分线CE交于点O．
(1)求证：∠AOC＝90°＋∠ABC；
(2)当∠ABC＝90°时，且AO＝3OD（如图2），判断线段AE，CD，AC之间的数量关系，并加以证明．
【答案】(1)见解析
(2)AE+CD=AC，证明见解析
【分析】（1）求出∠BAC+∠BCA=180°-∠ABC，根据角平分线定义求出∠OAC=∠BAC，∠OCA=∠BCA，即可求出∠OAC+∠OCA的度数，根据三角形内角和定理求出即可；
（3）在AC上分别截取AM、CN，使AM=AE，CN=CD，连接OM，ON，证△AEO≌△AMO，△DCO≌△NCO，推出∠EOA=∠MOA，∠CON=∠COD，OD=ON，求出∠MON=∠MOA=45°，根据角平分线性质求出MK=ML，据此计算即可求解．
（1）
证明：∵∠ABC+∠ACB+∠BAC=180°，
∴∠BAC+∠BCA=180°-∠ABC，
∵∠BAC的平分线AD与∠BCA的平分线CE交于点O．
∴∠OAC=∠BAC，∠OCA=∠BCA，
∴∠OAC+∠OCA=（∠BAC+∠BCA）=（180°-∠ABC）=90°-∠ABC，
∴∠AOC=180°-（∠OAC+∠OCA）=180°-（90°-∠ABC），
即∠AOC=90°+∠ABC；
（2）
解：AE+CD=AC，
证明：如图2，∵∠AOC=90°+∠ABC=135°，
∴∠EOA=45°，
在AC上分别截取AM、CN，使AM=AE，CN=CD，连接OM，ON，
则在△AEO和△AMO中，，
∴△AEO≌△AMO，
同理△DCO≌△NCO，
∴∠EOA=∠MOA，∠CON=∠COD，OD=ON，
∴∠EOA=∠MOA=∠CON=∠COD=45°，
∴∠MON=∠MOA=45°，
过M作MK⊥AD于K，ML⊥ON于L，
∴MK=ML，
S△AOM=AO×MK，S△MON=ON×ML，
∴，
∵，
∴，
∵AO=3OD，
∴，
∴，
∴AN=AM=AE，
∵AN+NC=AC，
∴AE+CD=AC．
【点睛】本题考查了全等三角形的性质和判定，角平分线定义和性质，三角形的面积，三角形内角和定理的应用，熟练掌握各性质定理是解答此题的关键．