77 第9章 第3课时　随机事件与概率-2025年高考数学一轮复习课件

这是一份77 第9章 第3课时　随机事件与概率-2025年高考数学一轮复习课件，共29页。PPT课件主要包含了考试要求，链接教材夯基固本，典例精研核心考点等内容，欢迎下载使用。
第3课时　随机事件与概率
了解随机事件发生的不确定性和频率的稳定性，了解概率的意义以及频率与概率的区别.
掌握古典概型及其计算公式，能计算古典概型中简单随机事件的概率．
理解事件间的关系与运算.
1．样本空间与样本点(1)样本点：随机试验E的每个可能的________称为样本点，常用ω表示．(2)样本空间：__________的集合称为试验E的样本空间，常用Ω表示样本空间．如果一个随机试验有n个可能结果ω1，ω2，…，ωn，则称样本空间Ω＝{ω1，ω2，…，ωn}为有限样本空间．
2．随机事件、必然事件与不可能事件(1)随机事件：________________称为随机事件，简称事件，随机事件一般用大写字母A，B，C，…表示．在每次试验中，当且仅当A中某个样本点出现时，称为事件A发生．(2)随机事件的特殊情形：必然事件Ω(含有全部样本点)、不可能事件∅(不含任何样本点)、基本事件(只包含一个样本点)．
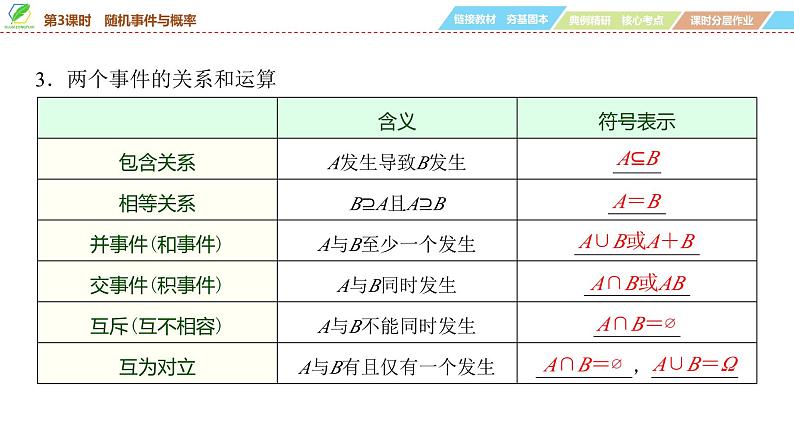
3．两个事件的关系和运算
6．概率的基本性质性质1：对任意的事件A，都有P(A)≥0.性质2：必然事件的概率为1，不可能事件的概率为0，即P(Ω)＝1，P(∅)＝0.性质3：如果事件A与事件B互斥，那么P(A∪B)＝______________．性质4：如果事件A与事件B互为对立事件，那么P(B)＝1－P(A)，P(A)＝_________．性质5：如果A⊆B，那么P(A)≤P(B)，由该性质可得，对于任意事件A，因为∅⊆A⊆Ω，所以0≤P(A)≤1.性质6：(一般概率加法公式)设A，B是一个随机试验中的两个事件，有P(A∪B)＝______________________．
P(A)＋P(B)－P(A∩B)
7．频率与概率(1)频率的稳定性一般地，随着试验次数n的增大，频率偏离概率的幅度会缩小，即事件A发生的频率fn(A)会逐渐______事件A发生的概率P(A)，我们称频率的这个性质为频率的稳定性．(2)频率稳定性的作用可以用频率fn(A)估计概率P(A)．(3)频率是概率的近似值，概率是频率的稳定值．
一、易错易混辨析(正确的打“√”，错误的打“×”)(1)必然事件一定发生．(　　)(2)两个事件的和事件发生是指这两个事件至少有一个发生．(　　)(3)在大量重复试验中，概率是频率的稳定值．(　　)(4)若A∪B是必然事件，则A与B是对立事件．(　　)
二、教材经典衍生1．(人教A版必修第二册P235练习T1改编)一个人打靶时连续射击两次，事件“至多有一次中靶”的对立事件是(　　)A．至少有一次中靶　　B．两次都中靶C．只有一次中靶 　D．两次都不中靶B　[“至多有一次中靶”的对立事件是“两次都中靶”．]
4．(人教A版必修第二册P245练习T1改编)已知P(A)＝0.4，P(B)＝0.2.(1)如果B⊆A，则P(A∪B)＝__________，P(AB)＝__________；(2)如果A，B互斥，则P(A∪B)＝__________，P(AB)＝__________．(1)0.4　0.2　(2)0.6　0　[(1)因为B⊆A，所以P(A∪B)＝P(A)＝0.4，P(AB) ＝P(B)＝0.2.(2)如果A，B互斥，则P(A∪B)＝P(A)＋P(B)＝0.4＋0.2＝0.6，P(AB)＝P(∅)＝0．]
考点一　随机事件与样本空间[典例1]　(1) 同时投掷两枚完全相同的骰子，用(x，y)表示结果，记事件A为“所得点数之和小于5”，则事件A包含的样本点的个数是(　　)A．3　　　B．4　　　C．5　　　D．6(2)从装有十个红球和十个白球的罐子里任取两球，下列情况中是互斥而不对立的两个事件的是(　　)A．至少有一个红球；至少有一个白球B．恰有一个红球；都是白球C．至少有一个红球；都是白球D．至多有一个红球；都是红球
(1)D　(2)B　[(1)事件A包含(1，1)，(1，2)，(1，3)，(2，1)，(2，2)，(3，1)，共6个样本点．故选D.(2)对于A，“至少有一个红球”可能为一个红球、一个白球，“至少有一个白球”可能为一个白球、一个红球，故两事件可能同时发生，所以不是互斥事件；对于B，“恰有一个红球”，则另一个必是白球，与“都是白球”是互斥事件，而任取两球还可能都是红球，故两事件不是对立事件；对于C，“至少有一个红球”为都是红球或一红一白，与“都是白球”显然是对立事件；对于D，“至多有一个红球”为都是白球或一红一白，与“都是红球”是对立事件．故选B.]名师点评　1．求样本空间中样本点个数的方法：(1)列举法；(2)树状图法；(3)排列组合法. 2．互斥事件与对立事件的关系对立事件是互斥事件，而互斥事件未必是对立事件．对立事件是互斥事件的充分不必要条件．
考点二　随机事件的频率与概率[典例2]　某超市为了解顾客的购物量及结算时间等信息，安排一名员工随机收集了在该超市购物的100位顾客的相关数据，如表所示．
已知这100位顾客中一次购物量超过8件的顾客占55%.(1)确定x，y的值，并估计顾客一次购物的结算时间的平均值；(2)估计一位顾客一次购物的结算时间不超过2分钟的概率．
名师点评　计算简单随机事件的频率或概率的步骤提醒：互斥事件的概率加法公式的适用条件是事件必须是互斥事件．重视利用对立事件的概率和等于1，用间接法求概率．
[跟进训练]2．某座水力发电站，每年六月份的发电量Y(单位：万千瓦时)与该河上游在六月份的降雨量X(单位：mm)有关．据统计，当X＝70时，Y＝460；X每增加10，Y增加5．已知近20年X的值为140，110，160，70，200，160，140，160，220，200，110，160，160，200，140，110，160，220，140，160.(1)完成近20年六月份降雨量频率分布表；
(2)假定今年6月份的降雨量与近20年六月份降雨量的分布规律相同，并将频率视为概率，求今年六月份该水力发电站的发电量低于490(万千瓦时)或超过530(万千瓦时)的概率．
考点三　古典概型[典例3]　有编号为A1，A2，…，A10的10个零件，测量其直径(单位：cm)，得到下面数据：其中直径在区间[1.48，1.52]内的零件为一等品．(1)从上述10个零件中，随机抽取1个，求这个零件为一等品的概率；(2)从这些一等品中，随机抽取2个零件．①用零件的编号列出样本空间；②求这2个零件直径相等的概率．
名师点评　利用公式法求解古典概型问题的步骤提醒：若样本点个数不多，要列出样本空间，若样本点个数多，用排列组合方法求．
巩固课堂所学 · 激发学习思维夯实基础知识 · 熟悉命题方式自我检测提能 · 及时矫正不足
本节课掌握了哪些考点？本节课还有什么疑问点？
课时分层作业(六十五)