北师大版数学七上期末考试压轴题考点训练（三）（2份，原卷版+解析版）

这是一份北师大版数学七上期末考试压轴题考点训练（三）（2份，原卷版+解析版），文件包含北师大版数学七上期末考试压轴题考点训练三原卷版doc、北师大版数学七上期末考试压轴题考点训练三解析版doc等2份试卷配套教学资源，其中试卷共18页， 欢迎下载使用。
【详解】解：，
解得，，
∵k为整数，关于x的方程的解为正整数，
∴k-2=1或k-2=5，
解得，k=3或k=7，
故答案为：3或7．
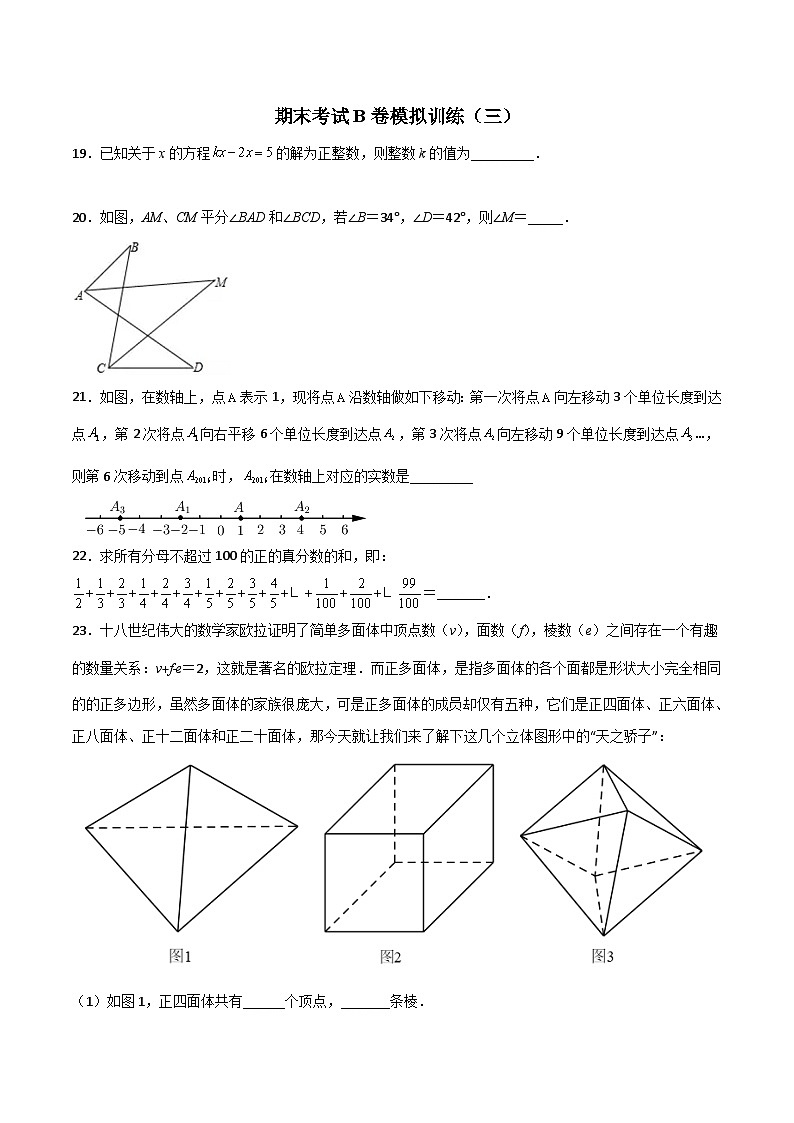
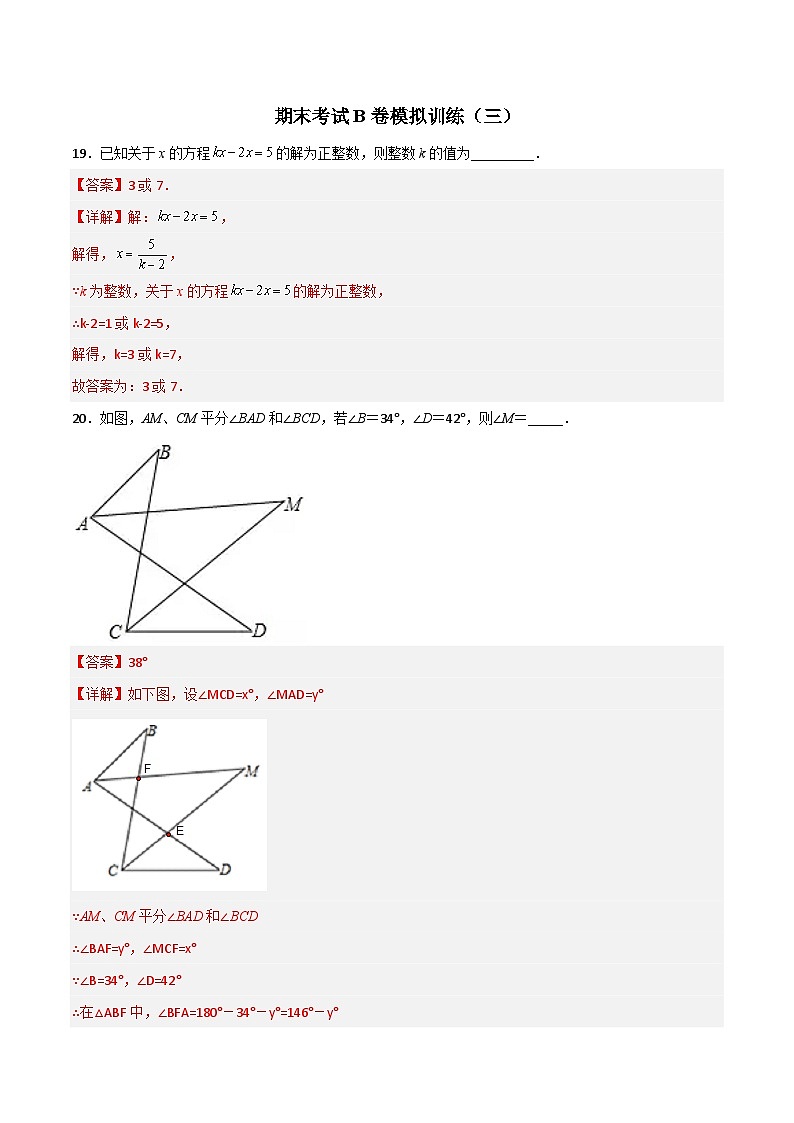
20．如图，AM、CM平分∠BAD和∠BCD，若∠B＝34°，∠D＝42°，则∠M＝_____．
【答案】38°
【详解】如下图，设∠MCD=x°，∠MAD=y°
∵AM、CM平分∠BAD和∠BCD
∴∠BAF=y°，∠MCF=x°
∵∠B=34°，∠D=42°
∴在△ABF中，∠BFA=180°－34°－y°=146°－y°
在△CED中，∠CED=180°－42°－x°=138°－x°
∴∠CFM=∠AFB=146°－y°，∠AEM=∠CED=138°－x°
∴在△AME中，y°+∠M+138°－x°=180°
在△FMC中，x°+146°－y°+∠M=180°
约掉x、y得，∠M=38°
故答案为：38°
21．如图，在数轴上，点表示1，现将点沿数轴做如下移动：第一次将点向左移动3个单位长度到达点，第2次将点向右平移6个单位长度到达点，第3次将点向左移动9个单位长度到达点…，则第6次移动到点时，在数轴上对应的实数是_________
【答案】3025
【详解】第一次点向左移动3个单位长度至点，则表示的数，1-3=-2；
第2次从点向右移动6个单位长度至点，则表示的数为：-2+6=4；
第3次从点向左移动9个单位长度至点，则表示的数为4-9=-5；
第4次从点向右移动12个单位长度至点，则表示的数为-5+12=7；
第5次从点向左移动15个单位长度至点，则表示的数为7-15=-8；
第6次从点向左移动18个单位长度至点，则表示的数为-8+18=10；
……；
发现序号是奇数的点在负半轴上，
，
，
，
发现序号是偶数的点在正半轴上，
，
，
，
，
则点表示：
22．求所有分母不超过100的正的真分数的和，即：＝_______．
【答案】2475
【详解】解：
＝．
＝
＝＝＝＝2475．
故答案为：2475．
23．十八世纪伟大的数学家欧拉证明了简单多面体中顶点数（v），面数（f），棱数（e）之间存在一个有趣的数量关系：v+f﹣e＝2，这就是著名的欧拉定理．而正多面体，是指多面体的各个面都是形状大小完全相同的的正多边形，虽然多面体的家族很庞大，可是正多面体的成员却仅有五种，它们是正四面体、正六面体、正八面体、正十二面体和正二十面体，那今天就让我们来了解下这几个立体图形中的“天之骄子”：
（1）如图1，正四面体共有______个顶点，_______条棱．
（2）如图2，正六面体共有______个顶点，_______条棱．
（3）如图3是某个方向看到的正八面体的部分形状（虚线被隐藏），正八面体每个面都是正三角形，每个顶点处有四条棱，那么它共有_______个顶点，_______条棱．
（4）当我们没有正12面体的图形时，我们可以根据计算了解它的形状：我们设正12面体每个面都是正n（n≥3）边形，每个顶点处有m（m≥3）条棱，则共有12n÷2＝6n条梭，有12n÷m＝个顶点．欧拉定理得到方程：+12﹣6n＝2，且m，n均为正整数，
去掉分母后：12n+12m﹣6nm＝2m，
将n看作常数移项：12m﹣6nm﹣2m＝﹣12n，
合并同类项：（10﹣6n）m＝﹣12n，
化系数为1：m＝，
变形：，
＝，
＝，
＝，
＝．
分析：m（m≥3），n（n≥3）均为正整数，所以是正整数，所以n＝5，m＝3，即6n＝30，．
因此正12面体每个面都是正五边形，共有30条棱，20个顶点．
请依据上面的方法或者根据自己的思考得出：正20面体共有_____条棱；_______个顶点．
【答案】（1）4；6；（2）8；12；（3）6；12；（4）30；12．
【详解】解：（1）如图1，正四面体又四个面，每个面有三条边，每个顶点处有三条棱，
共有4×3÷3=4个顶点，
共有4个顶点，每个顶点处有3条棱，每两点重复一条，
正四面体共有4×3÷2=6条棱．
故答案为4；6；
（2）如图2，正六面体有六个面，每个面四条棱，每个顶点处有三条棱，
共有6×4÷3=8个顶点，
正六面体共8个顶点，每个顶点处有3条棱，每两点重复一条，
正六面体共有8×3÷2=12条棱．
故答案为：8；12；
（3）如图3正八面体每个面都是正三角形，每个顶点处有四条棱，有八个面，每个面有三棱，每个顶点处有四条棱，
共有8×3÷4=6个顶点，
它共有6个顶点，每个顶点处有四条棱，6×4÷2=12条棱．
故答案为：6；12；
（4）正20面体每个面都是正n（n≥3）边形，每个顶点处有m（m≥3）条棱，则共有20n÷2＝10n条棱，有20n÷m＝个顶点．欧拉定理得到方程：+20﹣10n＝2，且m，n均为正整数，
去掉分母后：20n+20m﹣10nm＝2m，
将n看作常数移项：20m﹣10nm﹣2m＝﹣20n，
合并同类项：（18﹣10n）m＝﹣20n，
化系数为1：m＝，
变形：＝＝＝＝．
分析：m（m≥3），n（n≥3）均为正整数，所以是正整数，所以n＝3，m＝5，即10n＝30，．
正20面体共有30条棱；12个顶点．故答案为：30；12．
24．数轴上有A，B，C三点，A，B表示的数分别为m，n，点C在B的右侧，．
(1)如图1，若多项式是关于x的二次三项式，请直接写出m，n的值：
(2)如图2，在（1）的条件下，长度为1的线段（E在F的左侧）在A，B之间沿数轴水平滑动（不与A，B重合），点M是的中点，N是的中点，在滑动过程中，线段的长度是否发生变化，请判断并说明理由；
(3)若点D是的中点．
①直接写出点D表示的数____________（用含m，n的式子表示）；
②若，试求线段的长．
【答案】(1)，；(2)不变化，理由见解析；(3)①；②
【详解】（1）解：由题可知，n-1=0，7+m=2，
∴，
故答案为：，
（2）解：MN的长不发生变化，理由如下：
由题意，得点C表示的数为3，
设点E表示的数为x，则点F表示的数为
∴ ， ， ， ， ，，
∵点M是的中点，N是的中点
∴，
即
（3）解：①∵A，B表示的数分别为m，n
又点C在B的右侧
∴AB=n-m
∵
∴AC= n-m+2
∵点D是的中点
∴AD=AC= （n-m+2）
∴D表示的数为：m+ （n-m+2）=
②依题意，点C表示的数分别为
∴，
∴，
∵
即
当时．
∵
∴不符合题意，舍去
当时．
综上所述，线段的长为.
25．对数轴上的点P进行如下操作：将点P沿数轴水平方向，以每秒m个单位长度的速度，向右平移n秒，得到点，称这样的操作为点的“m速移”点称为点的“m速移”点．
(1)点A、B在数轴上对应的数分别是a、b，且．
①若点A向右平移n秒的“5速移”点与点B重合，求n；
②若点A向右平移n秒的“2速移”点与点B向右平移n秒的“1速移”点重合，求n；
(2)数轴上点M表示的数为1，点C向右平移3秒的“2速移”点为点，如果C、M、三点中有一点是另外两点连线的中点，求点C表示的数；
(3)数轴上E，F两点间的距高为3，且点E在点F的左侧，点E向右平移2秒的“x速移”点为点，点F向右平移2秒的“y速移”点为点，如果，请直接用等式表示x，y的数量关系．
【答案】(1)①4；②20；(2)−11，−2或7；(3)y−x＝3
【详解】（1）解：∵|a＋5|≥0， ≥0，，
∴a＋5＝0，b−15＝0，
∴a＝−5，b＝15．
①根据题意得：−5＋5n＝15，
∴n＝4；
②点 表示的数为−5＋2n，点 表示的数为15＋n，
根据题意得−5＋2n＝15＋n，
∴n＝20；
（2）解：设点C表示的数为c，则点 表示的数为c＋6，
若点 是CM的中点，则c＋1＝2（c＋6），解得c＝−11；
若点M是 的中点，则c＋c＋6＝2，解得c＝−2；
若点C是 的中点，则1＋c＋6＝2c，解得c＝7；
综上所述，点C表示的数为−11，−2或7；
（3）解：设点E表示的数为e，点F表示的数为f，
则点 表示的数为e＋2x，点 表示的数为f＋2y，f−e＝3，
∵E'F'＝3EF，
∴f＋2y−（e＋2x）＝3×3，
∴y−x＝3．
26．一副三角板按如图1所示放置，边在直线上，．
(1)求图1中的度数；
(2)如图2，将三角板绕点O顺时针旋转，转速为，同时将三角板绕点O逆时针旋转，转速为，当旋转到射线上时，两三角板都停止转动．设转动时间为．
①在范围内，当时，求t的值；
②如图3，旋转过程中，作的角平分线，当时．直接写出时间的值．
【答案】(1)(2)①2s；②s或s或s．
【详解】（1）解： ，
（2）解：① 则重合时的时间为：（s），
当时，

解得： 所以当旋转2s时，
②当旋转到射线上时，（s），
当时，结合①可得
当重合时，（s），重合时，（s），如图，
所以当时，
当重合时，（s），如图，
当时，



平分 解得：
当重合时，（s），
当时，如图，



平分


解得： 不符合题意，舍去，
当重合时，（s），
当



平分


解得：
如图，当再次重合时，（s），
当时，
如图，当重合时，（s）
当时，



平分

，解得：
综上：当时，s或s或s．