河北省磁县2024-2025学年八年级（上）数学期末模拟测试（含答案及详解）

这是一份河北省磁县2024-2025学年八年级（上）数学期末模拟测试（含答案及详解），共24页。试卷主要包含了选择题等内容，欢迎下载使用。
1. 下列图形中，轴对称图形的个数是（ ）
A. 1个B. 2个C. 3个D. 4个
2. 下列图形具有稳定性的是（ ）
A. B. C. D.
3. 刘零想做一个三角形的框架，她有两根长度分别为6cm和8cm的细木条，需要将其中一根木条分为两段，如果不考虑损耗和接头部分，那么可以分成两段的是（ ）
A. 6cm的木条B. 8cm的木条C. 两根都可以D. 两根都不行
4. 分式﹣可变形为（ ）
A. ﹣B. C. ﹣D.
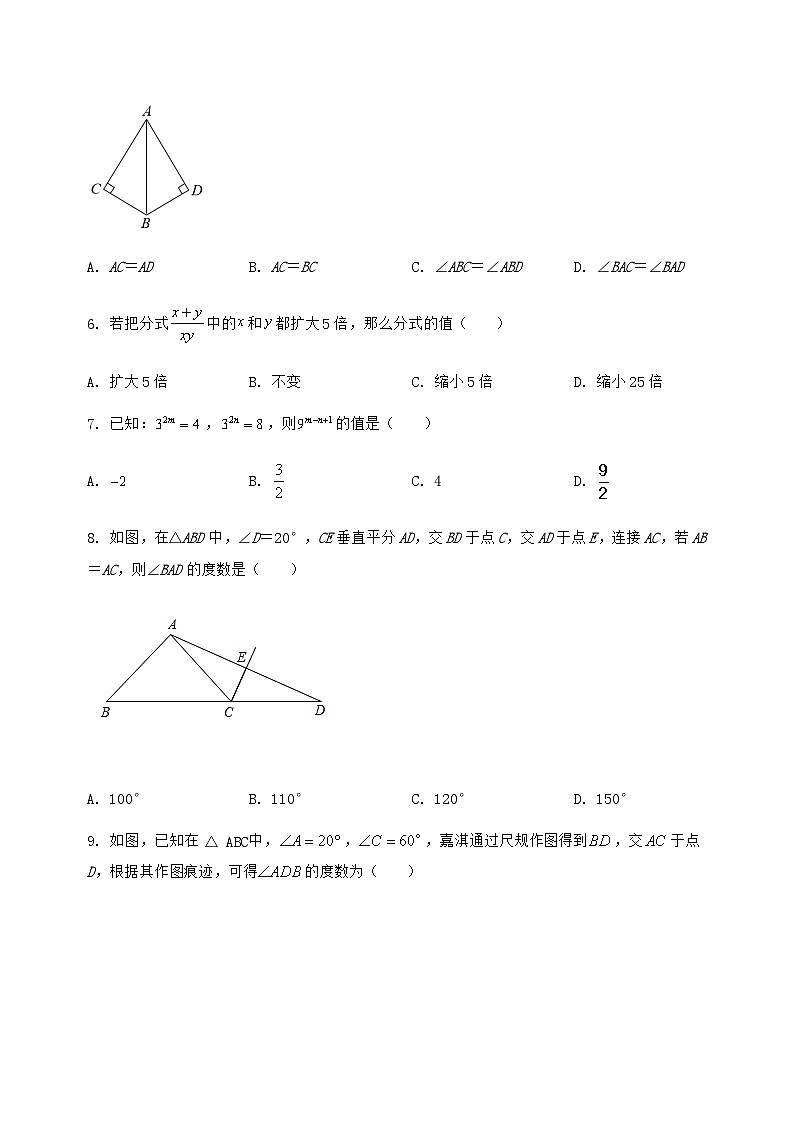
5. 如图，∠C＝∠D＝90°，添加一个条件，可使用“HL”判定Rt△ABC与Rt△ABD全等．以下给出的条件适合的是( )
A. AC＝ADB. AC＝BCC. ∠ABC＝∠ABDD. ∠BAC＝∠BAD
6. 若把分式中的和都扩大5倍，那么分式的值（ ）
A. 扩大5倍B. 不变C. 缩小5倍D. 缩小25倍
7. 已知：，，则的值是（ ）
A. B. C. 4D.
8. 如图，在△ABD中，∠D＝20°，CE垂直平分AD，交BD于点C，交AD于点E，连接AC，若AB＝AC，则∠BAD的度数是（ ）
A. 100°B. 110°C. 120°D. 150°
9. 如图，已知在△ABC中，，，嘉淇通过尺规作图得到，交于点D，根据其作图痕迹，可得的度数为（ ）
A. 120°B. 110°C. 100°D. 98°
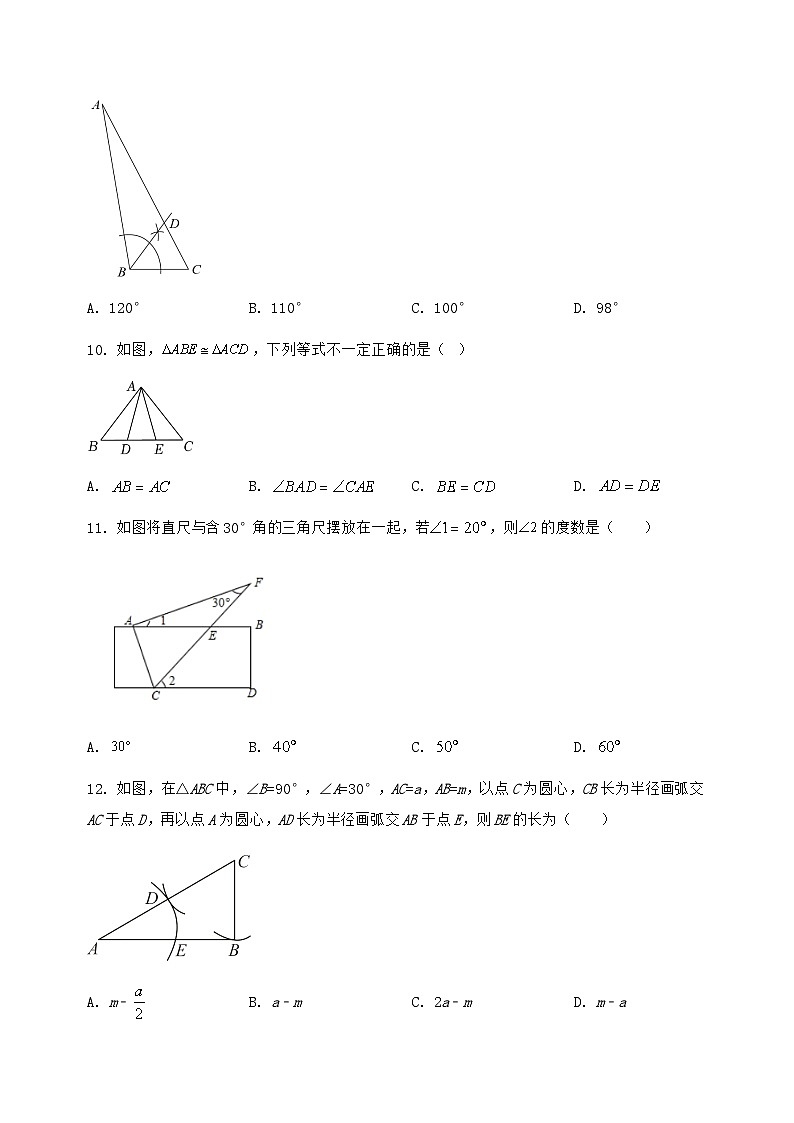
10. 如图，，下列等式不一定正确的是（ ）
A. B. C. D.
11. 如图将直尺与含30°角的三角尺摆放在一起，若，则的度数是（ ）
A. B. C. D.
12. 如图，在△ABC中，∠B=90°，∠A=30°，AC=a，AB=m，以点C为圆心，CB长为半径画弧交AC于点D，再以点A为圆心，AD长为半径画弧交AB于点E，则BE的长为（ ）
A. m﹣B. a﹣mC. 2a﹣mD. m﹣a
13. 为半径画弧，交O′A′于点C′；
（3）以点C'为圆心，CD长为半径画弧，与第（2）步中所画的弧相交于点D′；
（4）过点D'画射线O′B′，则∠A′O′B′＝∠AOB．
小聪作法正确的理由是（ ）
A. 由SSS可得△O′C′D′≌△OCD，进而可证∠A′O′B′＝∠AOB
B. 由SAS可得△O′C′D′≌△OCD，进而可证∠A′O′B′＝∠AOB
C. 由ASA可得△O′C′D′≌△OCD，进而可证∠A′O′B′＝∠AOB
D. 由“等边对等角”可得∠A′O′B′＝∠AOB
14. △ABC中，∠C=90°，∠A的平分线交BC于点D，如果AB=8，CD=3，则△ABD的面积为（ ）
A. 24B. 12C. 8D. 6
15. 如图，将长方形ABCD的各边向外作正方形，若四个正方形周长之和为24，面积之和为12，则长方形ABCD的面积为（ ）
A. 4B. C. D. 6
16. 如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P1，P2，P3，P4四个点中找出符合条件的点P，则点P有（ ）

A. 1个B. 2个C. 3个D. 4个
二.填空题(本大题共3题，总计 12分)
17. 请写出一个运算式子，使运算结果等于．你写的运算式子是______．
18. 已知三角形的三边长分别为3，5，x，则化简式子|x－2|＋|x－9|＝___．
19. 如图，已知△ABC中，，直角的顶点P是的中点，两边、分别交、于点E、F，给出以下四个结论：
①；
②是等腰直角三角形；
③；
④当在△ABC内绕顶点P旋转时（点E不与A、B重合），．
上述结论中始终正确有__________（填序号）．
三.解答题(共7题，总计66分，解答应写出文字说明、证明过程或演算步骤)
20. 把下列各式分解因式：
（1）4a2﹣1；
（2）3a2﹣6ab+3b2
（3）a2（x﹣y）﹣4x+4y
（4）m2﹣17m﹣38
21. 先化简，再求值：,其中-2x2,请从x的范围中选入一个你喜欢的值代入，求此分式的值.
22. 如图1，网格中的每一个正方形的边长为1，△ABC为格点三角形（点A、B、C在小正方形的顶点上），直线m为格点直线（直线m经过小正方形的格点）．
（1）如图1，作出△ABC关于直线m轴对称图形△A′B′C′；
（2）如图2，在直线m上找到一点P，使PA+PB的值最小；
（3）如图3，仅用直尺将网格中的格点三角形ABC的面积三等分，并将其中的一份用铅笔涂成阴影．
（4）如图4，仅用直尺作出三角形ABC的边AB上的高，简单说明你的理由．
23. 如图，ΔABC，ΔADE均是等边三角形，点B，D，E三点共线，连按CD，CE；且CD⊥BE．
（1）求证：BD=CE；
（2）若线段DE=3，求线段BD的长．
24. 我阅读：类比于两数相除可以用竖式运算，多项式除以多项式也可以用竖式运算，其步骤是：
（1）把被除式和除式按同一字母的降幂排列（若有缺项用零补齐）．
（2）用竖式进行运算．
（3）当余式的次数低于除式的次数时，运算终止，得到商式和余式．我会做：请把下面解答部分中的填空内容补充完整．求的商式和余式．
解：
答：商式是，余式是（ ）
我挑战：已知能被整除，请直接写出a、b的值．
25. 在今年新冠肺炎防疫工作中，某公司购买了、两种不同型号口罩，已知型口罩的单价比型口罩的单价多1.5元，且用8000元购买型口罩的数量与用5000元购买型口罩的数量相同．
（1）、两种型号口罩的单价各是多少元？
（2）根据疫情发展情况，该公司还需要增加购买一些口罩，增加购买型口罩数量是型口罩数量的2倍，若总费用不超过3800元，则增加购买型口罩的数量最多是多少个？
26.
（1）【自主学习】填空：
如图1，点是的平分线上一点，点A在上，用圆规在上截取，连接，可得 ，其理由根据是 ；
（2）【理解运用】如图2，在中，，，平分，试判断和、之间的数量关系并写出证明过程．
（3）【拓展延伸】如图3，在中，，，分别是，的平分线，，交于点，若，，请直接写出的长．
磁县2024-2025学年八年级（上）数学期末模拟测试
参考答案及解析
一.选择题
1.【答案】：C
【解析】：解：第1个是轴对称图形；
第2个是轴对称图形；
第3个不是轴对称图形；
第4个是轴对称图形；
故选C．
【画龙点睛】本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
2.【答案】：A
【解析】：A.具有稳定性，符合题意；
B.不具有稳定性，故不符合题意；
C.不具有稳定性，故不符合题意；
D.不具有稳定性，故不符合题意，
故选：A．
3.【答案】：B
【解析】：解：利用三角形的三边关系可得应把8cm的木条截成两段，
如将8cm的线段分成3cm和5cm或4cm和4cm，所截成的两段线段之和大于6，所以，可以，
而6cm的线段无论如何分，分成的两段线段之和都小于8，所以，不可以．
故选：B．
4.【答案】：B
【解析】： 可变式为
∴B正确
故选B
5.【答案】：A
【解析】：解： 需要添加条件为：BC= BD或AC= AD,理由为:
若添加的条件为：BC= BD
在Rt△ABC与Rt△ABD中,

∴Rt△ABC≌Rt△ABD(HL) ;
若添加的条件为：AC=AD
在Rt△ABC与Rt△ABD中,
∴Rt△ABC≌Rt△ABD( HL).
故选：A.
6.【答案】：C
【解析】：把分式中的和都扩大5倍，
即，
即得到的式子比原式缩小了5倍．
故选：C
7.【答案】：D
【解析】：
∴= =4÷8×9=
故选：D
8.【答案】：C
【解析】：解：∵CE垂直平分AD，
∴，
∴，
∴，
∵AB＝AC，
∴，
∴，
∴，
故选：C．
9.【答案】：B
【解析】：根据作图痕迹可知，是∠ABC的平分线，
∵，，
∴
∵是∠ABC的平分线，
∴
∴
故选：B．
10.【答案】：D
【解析】：，
，，，，
，
，
即只有选项符合题意，选项A、选项B、选项C都不符合题意；
故选：D．
11.【答案】：C
【解析】：如图，
∵∠BEF是△AEF的外角，∠1=20，∠F=30，
∴∠BEF=∠1+∠F=50，
∵AB∥CD，
∴∠2=∠BEF=50，
故选：C．
12.【答案】：A
【解析】：解：∵∠B=90°，∠A=30°，AC=a，
∴BC=AC=a，
∵以点C为圆心，CB长为半径画弧交AC于点D，
∴CD=BC=a，
∵以点A为圆心，AD长为半径画弧交AB于点E，
∴AD=AE=AC-CD=a，
∵AB=m，
∴BE=AB-AE=m-a，
故选：A．
13.【答案】：A
【解析】：解：由作图得OD＝OC＝OD′＝OC′，CD＝C′D′，
则根据“SSS”可判断△C′O′D′≌△COD．
故选：A．
14.【答案】：B
【解析】：作DE⊥AB于E，
∵AD平分∠BAC，DE⊥AB，DC⊥AC，
∴DE=CD=3，
∴△ABD的面积为×3×8=12，
故选：B．
15.【答案】：B
【解析】：解：设AB＝a，AD＝b，由题意得8a＋8b＝24，2a2＋2b2＝12，
即a＋b＝3，a2＋b2＝6，
∴，
即长方形ABCD的面积为，
故选：B．
16.【答案】：C
【解析】：要使△ABP与△ABC全等，
必须使点P到AB的距离等于点C到AB的距离，
即3个单位长度，
所以点P的位置可以是P1，P2，P4三个，
故选C．
二. 填空题
17.【答案】： （答案不唯一）
【解析】：．
故答案为∶（答案不唯一）．
【画龙点睛】本题考查了同底数幂相乘的法则，解题的关键是注意掌握同底数幂的运算法则．
18.【答案】： 7
【解析】：解：根据题意，得5−3