

所属成套资源:河北省各地区2024-2025学年八年级(上)数学期末模拟测试(含答案及详解)
河北省秦皇岛市海港区2024-2025学年八年级(上)数学期末模拟测试(含答案及详解)
展开
这是一份河北省秦皇岛市海港区2024-2025学年八年级(上)数学期末模拟测试(含答案及详解),共24页。试卷主要包含了选择题等内容,欢迎下载使用。
1. 下列图形中,是轴对称图形的是( )
A. B. C. D.
2. 下列运算正确是( )
A. B. C. D.
3. 最近科学家发现了一种病毒的长度约为0.00000456毫米,则数据0.00000456用科学记数法表示为( )
A. B. C. D.
4. 下列等式中,不成立的是( )
A. B.
C. D.
5. 若M=(x-3)(x-4),N=(x-1)(x-6),则M与N的大小关系为()
A. M>NB. M=NC. M<ND. 由x的取值而定
6. 某同学用5cm、7cm、9cm、13cm的四根小木棒摆出不同形状的三角形的个数为( )
A. 1B. 2C. 3D. 4
7. 若,则2n-3m的值是( )
A. -1B. 1C. 2D. 3
8. 中国首列商用磁浮列车平均速度为,计划提速,已知从A地到B地路程为,那么提速后从A地到B地节约的时间为( )
A. B. C. D.
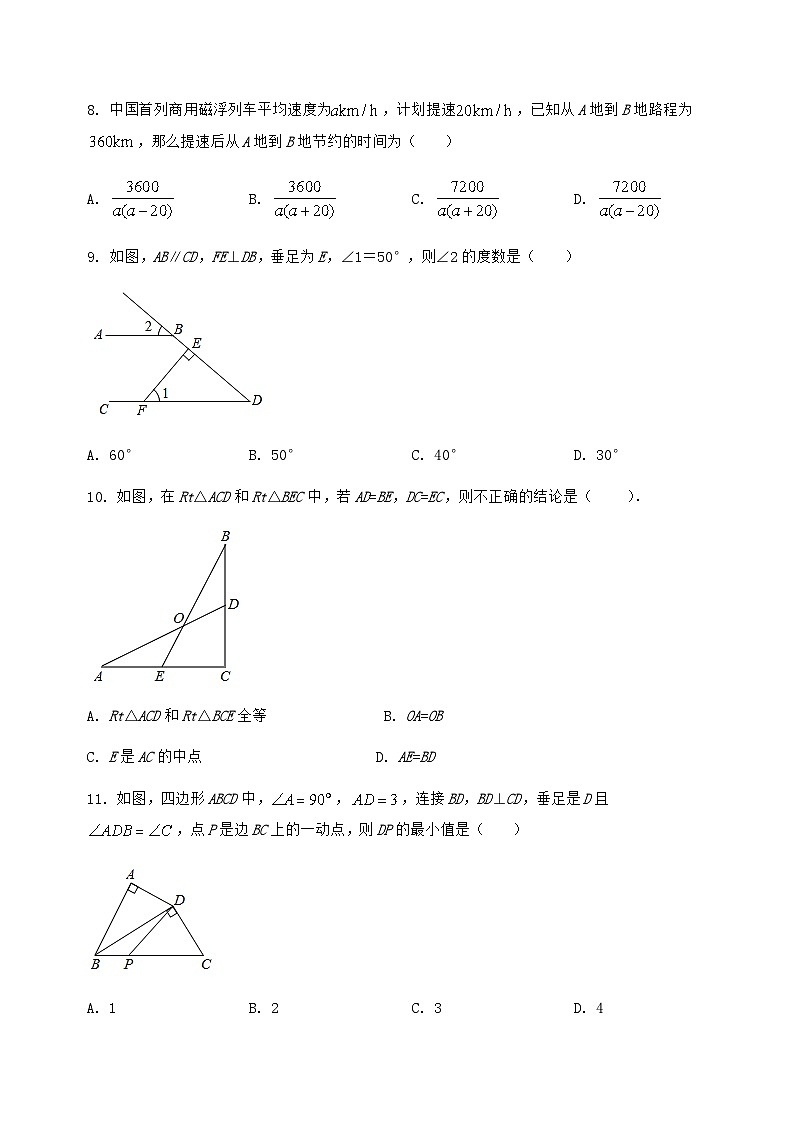
9. 如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( )
A. 60°B. 50°C. 40°D. 30°
10. 如图,在Rt△ACD和Rt△BEC中,若AD=BE,DC=EC,则不正确的结论是( ).
A. Rt△ACD和Rt△BCE全等B. OA=OB
C. E是AC的中点D. AE=BD
11. 如图,四边形ABCD中,,,连接BD,BD⊥CD,垂足是D且,点P是边BC上的一动点,则DP的最小值是( )
A. 1B. 2C. 3D. 4
12. 在ΔABC中给定下面几组条件:
①∠ACB=30°,BC=4cm,AC=5cm ②∠ABC=30°,BC=4cm,AC=3cm
③∠ABC=90°,BC=4cm,AC=5cm ④∠ABC=120°,BC=4cm,AC=5cm
若根据每组条件画图,则ΔABC不能够唯一确定的是( )
A. ①B. ②C. ③D. ④
13. 若是完全平方式,则m的值为( )
A. 3B. C. 7D. 或7
14. 如图,△ABC中,,,,则△ABC的周长为( )
A. 9B. 8C. 6D. 12
15. 如图,在△ABC,△ADE中,,,,C,D,E三点在同一条直线上,连接.以下四个结论中:①;②;③;④.正确的个数是( )
A. 1个B. 2个C. 3个D. 4个
16. 如图,已知AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE与CF交于点D,则下列结论中不正确的是( )
A. △ABE≅△ACFB. △BDF≅△CDE
C. 点D在平分线上D. 点D是CF的中点
二.填空题(本大题共3题,总计 12分)
17. 方程=的解为x=___.
18. 已知a和b两个有理数,规定一种新运算“*”为:a*b=(其中a+b≠0),若m*=﹣,则m=______.
19. 如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则周长的最小值为_______.
三.解答题(共7题,总计66分,解答应写出文字说明、证明过程或演算步骤)
20. 计算:
(1)(﹣a2)3÷a4+(a+2)(2a﹣3).
(2)(3a+2b﹣5)(3a﹣2b+5)
21. 先化简,再求值:
(1),其中.
(2),再求当与互为相反数时,代数式的值.
22. 如图1,网格中的每一个正方形的边长为1,△ABC为格点三角形(点A、B、C在小正方形的顶点上),直线m为格点直线(直线m经过小正方形的格点).
(1)如图1,作出△ABC关于直线m轴对称图形△A′B′C′;
(2)如图2,在直线m上找到一点P,使PA+PB的值最小;
(3)如图3,仅用直尺将网格中的格点三角形ABC的面积三等分,并将其中的一份用铅笔涂成阴影.
(4)如图4,仅用直尺作出三角形ABC的边AB上的高,简单说明你的理由.
23. 如图,在△ABC中,射线AM平分∠BAC.
(1)尺规作图(不写作法,保留作图痕迹)作BC的中垂线,与AM相交于点G,连接BG、CG;
(2)在(1)条件下,∠BAC和∠BGC有何数量关系?并证明你的结论.
24. 实践与探索
如图1,边长为的大正方形有一个边长为的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示)
(1)上述操作能验证的等式是__________;(请选择正确的一个)
A. B. C.
(2)请应用这个公式完成下列各题:
①已知,,则__________.
②计算:
25. 某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值;
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餍椅的总数量不超过200张.该商场计划将餐桌成套(一张餐桌和四张餐椅配成一套)销售,多余的桌或椅以零售方式销售.请问当进货量最大时获得的利润是多少?
26. 已知M是等边△ABC的边BC上的点.
(1)如图①,过点M作MN∥CA,交AB于点N,求证:BM = BN;
(2)如图②,连接AM,过点M作∠AMH = 60°,MH与∠ACB的邻补角的平分线交于点H,过点H作HD⊥BC,交BC延长线于点D.
(ⅰ)求证:MA = MH;
(ⅱ)直接写出CB,CM,CD之间的数量关系式.
秦皇岛市海港区2024-2025学年八年级(上)数学期末模拟测试
参考答案及解析
一.选择题
1.【答案】:B
【解析】:轴对称的定义:如果一个图形沿一条直线折叠,直线两旁的部分能够相互重合,则称该图形为轴对称图形.
根据定义,B选项的图形符合题意.
故选B.
2.【答案】:B
【解析】:A选项,,故不符合题意;
B选项,,故符合题意;
C选项,,故不符合题意;
D选项,,故不符合题意;
故选:B.
3.【答案】:C
【解析】:数据0.00000456用科学记数法表示为:.
故选:C.
4.【答案】:C
【解析】:A、,故A不符合题意.
B、,故B不符合题意.
C、,故C符合题意.
D、,故D不符合题意.
故选:C.
5.【答案】:A
【解析】:解: M=(x-3)(x-4)=
N=(x-1)(x-6)=
即:
故选:A.
6.【答案】:C
【解析】:解:四条木棒的所有组合:5,7,9和5,9,13和5,7,13和7,9,13;
只有5,7,9和5,9,13和7,9,13能组成三角形.
故选:C.
7.【答案】:B
【解析】:解:∵,
∴,
∴,
∴.
故选:B
8.【答案】:C
【解析】:解:由题意可得
故选:C.
9.【答案】:C
【解析】:解:∵FE⊥DB,
∵∠DEF=90°,
∵∠1=50°,
∴∠D=90°﹣50°=40°,
∵AB∥CD,
∴∠2=∠D=40°.
故选C.
10.【答案】:C
【解析】:解:A.∵∠C=∠C=90°,
∴△ACD和△BCE是直角三角形,
在Rt△ACD和Rt△BCE中,
∵AD=BE,DC=CE,
∴Rt△ACD≌Rt△BCE(HL),正确;
B.∵Rt△ACD≌Rt△BCE,
∴∠B=∠A,CB=CA,
∵CD=CE,
∴AE=BD,
在△AOE和△BOD中,
∵
∴△AOE≌△BOD(AAS),
∴AO=OB,正确,不符合题意;
C.AE=BD,CE=CD,不能推出AE=CE,错误,符合题意;
D.∵Rt△ACD≌Rt△BCE,
∴∠B=∠A,CB=CA,
∵CD=CE,
∴AE=BD,正确,不符合题意.
故选C.
11.【答案】:C
【解析】:解:∵BD⊥CD,∠A=90°
∴∠ABD+∠ADB=90°,
∠CBD+∠C=90°,
∵∠ADB=∠C ,
∴∠ABD=∠CBD,
由垂线段最短得,DP⊥BC时DP最小,
此时,DP=AD=3.
故选:C.
12.【答案】:B
【解析】:解:①BC=4cm,AC=5cm,∠ACB=30°,满足“SAS”,所以根据这组条件画图,△ABC唯一;
②BC=4cm,AC=3cm,∠ABC=30°,根据这组条件画图,△ABC可能为锐角三角形,也可为钝角三角形;
③BC=4cm,AC=5cm,∠ABC=90°;满足“HL”,所以根据这组条件画图,△ABC唯一;
④BC=4cm,AC=5cm,∠ABC=120°,根据这组条件画图,△ABC唯一.
所以,ΔABC不能够唯一确定的是②.
故选:B
13.【答案】:D
【解析】:∵关于x的二次三项式是一个完全平方式,
∴m-2=±1×5,
∴m=7或-3,故D正确.
故选:D.
【画龙点睛】本题主要考查了完全平方公式的应用,解答此题的关键是要明确:.
14.【答案】:D
【解析】:解:在△ABC中,
, ,
,
,
∴△ABC为等边三角形,
,
∴△ABC的周长为:,
故答案为:D.
15.【答案】:C
【解析】:解:①∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,
∵在△BAD和△CAE中,,
∴△BAD≌△CAE(SAS),
∴BD=CE,
∵
∴
故本选项错误;
②∵△ABC为等腰直角三角形,
∴∠ABC=∠ACB=45°,
∴∠ABD+∠DBC=45°,
∵△BAD≌△CAE,
∴∠ABD=∠ACE,
∴∠ACE+∠DBC=45°,
故本选项正确;
③∵∠ABD+∠DBC=45°,
∴∠ACE+∠DBC=45°,
∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°,
则BD⊥CE,
故本选项正确;
④∵∠BAC=∠DAE=90°,
∴∠BAE+∠DAC=360°-90°-90°=180°,
故此选项正确,
综上,三个结论是正确的,
故选:C.
16.【答案】:D
【解析】:解:A、∵AB=AC,BE⊥AC于E,CF⊥AB于F,∠A=∠A∴△ABE≌△ACF(AAS),正确;
B∵△ABE≌△ACF,AB=AC∴BF=CE,∠B=∠C,∠DFB=∠DEC=90°∴△BDF≌△CDE(ASA),正确;
C、∵△ABE≌△ACF,AB=AC∴BF=CE,∠B=∠C,∠DFB=∠DEC=90°∴DF=DE故点D在∠BAC的平分线上,正确;
D、无法判定,错误;
故选D.
【画龙点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL. 注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
二. 填空题
17.【答案】: x=-3
【解析】:解:方程两边同乘以x(x-3),
得2x=x-3,
解得x=-3.
经检验:x=-3是原方程的解,
故答案为:x=-3.
18.【答案】:
【解析】:解:已知等式利用题中的新定义化简得: ,即
整理得:3(2m+3)=﹣5(2m﹣3),
去括号得:6m+9=﹣10m+15,
移项合并得:16m=6,
解得: ,
检验当时, ,
∴是分式方程的解,
则.
故答案为:.
19.【答案】: 10
【解析】:解:如图,连接,
是等腰三角形,点是边的中点,
,
,
解得,
是线段的垂直平分线,
点关于直线的对称点为点,
的长为的最小值,
周长的最小值.
故答案为:10.
三.解答题
20【答案】:
(1)a2+a﹣6;
(2)9a2﹣4b2+20b﹣25
【解析】:
【小问1详解】
解:(﹣a2)3÷a4+(a+2)(2a﹣3)
=﹣a6÷a4+2a2﹣3a+4a﹣6
=﹣a2+2a2﹣3a+4a﹣6
=a2+a﹣6;
【小问2详解】
解:(3a+2b﹣5)(3a﹣2b+5)
=[3a+(2b﹣5)][3a﹣(2b﹣5)]
=(3a)2﹣(2b﹣5)2
=9a2﹣(4b2﹣20b+25)
=9a2﹣4b2+20b﹣25.
【画龙点睛】本题考查了整式的混合运算,在进行运算时注意符号是否有变化.
21【答案】:
(1),;(2),.
【解析】:
解:(1)
当时,
原式
;
(2)
由题意得,
解得,
当时,
原式
.
【画龙点睛】本题考查整式的化简求值、分式的化简求值,涉及提公因式、完全平方公式、平方差公式等知识,是重要考点,难度较易,掌握相关知识是解题关键.
22【答案】:
(1)见解析 (2)见解析
(3)见解析 (4)见解析
【解析】:
【小问1详解】
如图所示,△A′B′C′即为所求作,
【小问2详解】
如图,点P即为所求作,
【小问3详解】
如图,即为所作,
【小问4详解】
如图,选择格点D、E,证明△ACD≌△BCE.于是,AC=BC.
选择格点Q,证明△ACQ≌△BCQ,于是,AQ=BQ.
∴CQ为线段AB的垂直平分线,设CQ与AB相交于点F,则CF为所要求的△ABC的边AB上的高.
23【答案】:
(1)详见解析;(2)∠BAC+∠BGC=180°,证明详见解析.
【解析】:
解:(1)线段BC的中垂线EG如图所示:
(2)结论:∠BAC+∠BGC=180°.
理由:在AB上截取AD=AC,连接DG.
∵AM平分∠BAC,
∴∠DAG=∠CAG,
在△DAG和△CAG中
∵
∴△DAG≌△CAG(SAS),
∴∠ADG=∠ACG,DG=CG,
∵G在BC的垂直平分线上,
∴BG=CG,
∴BG=DG,
∴∠ABG=∠BDG,
∵∠BDG+∠ADG=180°,
∴∠ABG+∠ACG=180°,
∵∠ABG+∠BGC+∠ACG+∠BAC=360°,
∴∠BAC+∠BGC=180°.
24【答案】:
(1)A;(2)①4;②5050
【解析】:
(1)图1表示,图2的面积表示,两个图形阴影面积相等,得到
故选A ;
(2)①
∵
∴,解得
②原式=(1002-992)+(982-972)+…+(42-32)+(22-12)
=(100+99)(100-99)+(98+97)(98-97)+…+(4+3)(4-3)+(2+1)(2-1)
=100+99+98+97+…+4+3+2+1
=101×50
=5050
【画龙点睛】本题考查了平方差公式的几何证明,题目较为简单,需要利用正方形和长方形的面积进行变形求解.
25【答案】:
(1)150
(2)当进货量最大时获得的利润是7200元
【解析】:
(1)根据题意确定等量关系列方程即可.
(2)首先设购进桌子的数量为x,求出其取值范围,再列出总利润和x的函数关系,根据一次函数性质求最大值即可.
【小问1详解】
解:根据题意,得:,解得:
经检验符合实际且有意义.
∴表中a的值为150.
【小问2详解】
解:设餐桌购进x张,则餐椅购进张,
依题意列:
解得:
设利润为W元,
则
∵
∴W随x的增大而增大
∴当 x=30时,W 有最大值
此时 .
答:当进货量最大时获得的利润是7200元.
【画龙点睛】本题考查了分式方程和一元一次不等式以及一次函数的性质,解题的关键是理解题意,找出等量关系列出方程,再根据一次函数性质求最大利润.
26【答案】:
(1)见解析 (2)(ⅰ)见解析;(ⅱ)BC CM 2CD
【解析】:
∴△AMN≌△MHC(ASA),
∴MA=MH;
(ⅱ)CB=CM+2CD;理由如下:
证明:如图2,过M点作MG⊥AB于G,
∵△AMN≌△MHC,
∴MN=HC,
∵△BMN为等边三角形,MG⊥AB
∴MN=MB,BM=2BG,
∴HC=BM,
△BMG和△CHD中
&∠B=∠HCD&∠MGB=∠HDC&HC=MB,
∴△BMG≌△CHD(AAS),
∴CD=BG,
∴BM=2CD,
所以BC=MC+2CD.
【画龙点睛】此题主要考查了等边三角形的性质,以及全等三角形的判定与性质,关键是正确作出辅助线,熟练掌握证明三角形全等的方法.原进价(元/张)
零售价(元/张)
成套售价(元/套)
餐桌
a
270
500元
餐椅
70
相关试卷
这是一份河北省秦皇岛市北戴河区2024-2025学年八年级(上)数学期末模拟测试(含答案及详解),共21页。试卷主要包含了选择题等内容,欢迎下载使用。
这是一份河北省涉县2024-2025学年八年级(上)数学期末模拟测试(含答案及详解),共25页。试卷主要包含了选择题等内容,欢迎下载使用。
这是一份河北省易县2024-2025学年八年级(上)数学期末模拟测试(含答案及详解),共22页。试卷主要包含了选择题等内容,欢迎下载使用。









