河北省平乡县2024-2025学年八年级（上）数学期末模拟测试（含答案及详解）

这是一份河北省平乡县2024-2025学年八年级（上）数学期末模拟测试（含答案及详解），共22页。试卷主要包含了选择题等内容，欢迎下载使用。
1. 下列防疫的图标中是轴对称图形的是（ ）
A. B. C. D.
2. 计算(4a3  12a2b  8a3b2) ÷ (4a2)的结果是（ ）
A. a  3b  2ab2B. a2 3b  2ab
C. a  2abD. 1.5a  3b
3. 在攻击人类的病毒中，某类新型冠状病毒体积较大，直径约为0.000 000 125米，含约3万个碱基， 拥有RNA病毒中最大的基因组，比艾滋病毒和丙型肝炎的基因组大三倍以上，比流感的基因组大两倍．0.000000125用科学记数法表示为( )
A. 1.25×10-6B. 1.25×10-7C. 1.25×106D. 1.25×107
4. 下列等式中，不成立的是（ ）
A. B.
C. D.
5. 等腰三角形的周长为13cm，其中一边长为3cm，则该等腰三角形的底边长为（ ）
A. 7cmB. 3cmC. 9cmD. 5cm
6. 若点，关于y轴对称，则点所在的象限是（ ）
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
7. 下列各式变形中，是因式分解的是（ ）
A. B.
C. D.
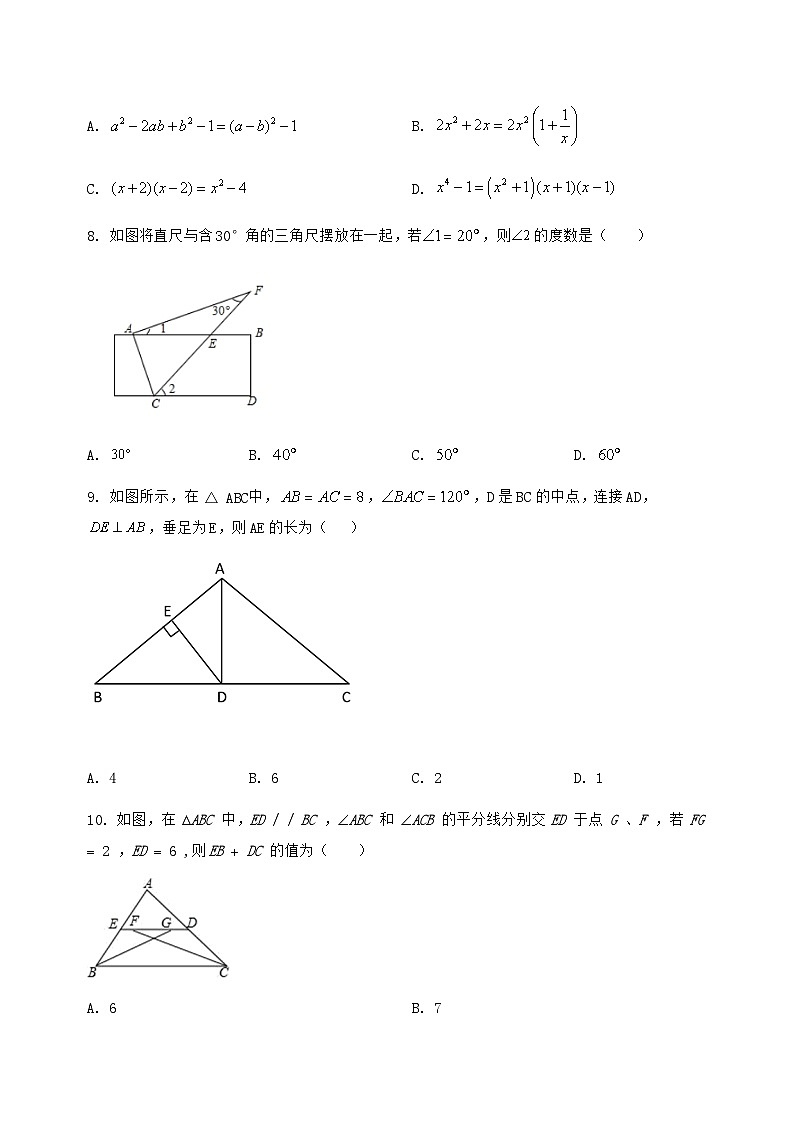
8. 如图将直尺与含30°角的三角尺摆放在一起，若，则的度数是（ ）
A. B. C. D.
9. 如图所示，在△ABC中，，，D是BC的中点，连接AD，，垂足为E，则AE的长为（ ）
A. 4B. 6C. 2D. 1
10. 如图，在 ABC 中，ED / / BC ，ABC 和 ACB 的平分线分别交 ED 于点 G 、F ，若 FG  2 ，ED  6 ,则EB  DC 的值为（ ）
A. 6B. 7
C. 8D. 9
11. 在ΔABC中给定下面几组条件：
①∠ACB=30°，BC=4cm，AC=5cm ②∠ABC=30°，BC=4cm，AC=3cm
③∠ABC=90°，BC=4cm，AC=5cm ④∠ABC=120°，BC=4cm，AC=5cm
若根据每组条件画图，则ΔABC不能够唯一确定的是（ ）
A. ①B. ②C. ③D. ④
12. 如图，在△ABC中，∠B=90°，∠A=30°，AC=a，AB=m，以点C为圆心，CB长为半径画弧交AC于点D，再以点A为圆心，AD长为半径画弧交AB于点E，则BE的长为（ ）
A. m﹣B. a﹣mC. 2a﹣mD. m﹣a
13. 如图，已知∠ABD=∠BAC，添加下列条件还不能判定△ABC≌△BAD的依据是（ ）
A. AC=BDB. ∠DAB=∠CBAC. ∠C=∠DD. BC=AD
14. 若关于x的分式方程－2＝无解，则m的值为（ ）
A. 0B. 2C. 0或2D. 无法确定
15. 已知甲、乙、丙均为x的一次多项式，且其一次项系数皆为正整数，若甲与乙相乘得，乙与丙相乘得，则甲、丙之积与乙的差是（ ）
A. B.
C. D.
16. 如图，已知AB=AC，BE⊥AC于点E，CF⊥AB于点F，BE与CF交于点D，则下列结论中不正确的是（ ）
A. △ABE≅△ACFB. △BDF≅△CDE
C. 点D在平分线上D. 点D是CF的中点
二.填空题(本大题共3题，总计 12分)
17. 因式分解：____________
18. 将下列多项式分解因式，结果中不含因式的是_________（填上你认为正确的序号）．①；②；③；④．
19. 丽丽在做一道计算题目的时候是这样分析的：这个算式里面每个括号内都是两数和的形式，跟最近学的乘法公式作比较，发现如果添加两数的差作为新的因式，就可以运用平方差公式进行运算，她尝试添了因式，很快得到计算结果．
①______________；
请参考丽丽的方法进行运算：
②的值为____________．
三.解答题(共7题，总计66分，解答应写出文字说明、证明过程或演算步骤)
20. （1）因式分解：；
（2）化简：．
21. 解分式方程：
（1）
（2）
22. 如图，△ABC的三个顶点的坐标分别是，，．
（1）在图中画出△ABC关于x轴对称的
（2）分别写出点A，B，C三点关于y轴对称的点，，的坐标；
（3）△ABC的面积为______．
23. 如图，AD平分∠BAC，∠EAD＝∠EDA，∠B＝54°．
（1）求∠EAC的度数；
（2）若∠CAD：∠E＝2：5；求∠E的度数．
24. 【阅读】下列是多项式因式分解的过程：．请利用上述方法解决下列问题．
【应用】
（1）因式分解：；
（2）若x>5，试比较与0的大小关系；
（3）【灵活应用】若，求的值．
25. 一水果店主分两批购进某一种水果，第一批所用资金为2400元，因天气原因，水果涨价，第二批所用资金是2700元，但由于第二批单价比第一批单价每箱多10元，以致购买的数量比第一批少25%．
（1）该水果店主购进第一批这种水果的单价是多少元？
（2）该水果店主计两批水果的售价均定为每箱40元，实际销售时按计划无损耗售完第一批后，发现第二批水果品质不如第一批，于是该店主将售价下降a%销售，结果还是出现了20%的损耗，但这两批水果销售完后仍赚了不低于1716元，求a的最大值．
26. 已知∠MAN=120°，点C是∠MAN的平分线AQ上的一个定点，点B，D分别在AN，AM上，连接BD．
【发现】
（1）如图1，若∠ABC=∠ADC=90°，则∠BCD= °，△CBD是 三角形；
【探索】
（2）如图2，若∠ABC+∠ADC=180°，请判断△CBD的形状，并证明你的结论；
【应用】
（3）如图3，已知∠EOF=120°，OP平分∠EOF，且OP=1，若点G，H分别在射线OE，OF上，且△PGH为等边三角形，则满足上述条件的△PGH的个数一共有 ．（只填序号）
①2个 ②3个 ③4个 ④4个以上
平乡县2024-2025学年八年级（上）数学期末模拟测试
参考答案及解析
一.选择题
1.【答案】：C
【解析】：解：轴对称图形定义：把一个图形沿某条直线对折，对折后直线两旁的部分能完全重合．发现A，B，D都不符合定义，所以A，B，D都错误，只有C符合，所以C正确．
故答案为C．
2.【答案】：A
【解析】：解：(4a3  12a2b  8a3b2) ÷ (4a2)
.
故选A
3.【答案】：B
【解析】：解：0.000000125=1.25×10-7，
故答案选：B
4.【答案】：C
【解析】：A、，故A不符合题意．
B、，故B不符合题意．
C、，故C符合题意．
D、，故D不符合题意．
故选：C．
5.【答案】：B
【解析】：当长是3cm的边是底边时，三边为3cm，5cm，5cm，等腰三角形成立；
当长是3cm的边是腰时，底边长是：13﹣3﹣3=7（cm），而3+3＜7，不满足三角形的三边关系．
故底边长：3cm．
故选：B．
6.【答案】：C
【解析】：解：∵点A（a，3）、点B (2，－b)关于y轴对称，
∴a=2，－b=3，
解得：a=－2，b=－3，
∴点M（a，b）在第三象限，
故选：C．
7.【答案】：D
【解析】：解：A、等式的右边不是整式的积的形式，故A错误；
B、等式右边分母含有字母不是因式分解，故B错误；
C、等式的右边不是整式的积的形式，故C错误；
D、是因式分解，故D正确；
故选D．
8.【答案】：C
【解析】：如图，
∵∠BEF是△AEF的外角，∠1=20，∠F=30，
∴∠BEF=∠1+∠F=50，
∵AB∥CD，
∴∠2=∠BEF=50，
故选：C．
9.【答案】：C
【解析】：解： ， ，D为BC中点，
，
，
，D为BC中点，
，
，
， ，
，
．
故答案为：C．
10.【答案】：C
【解析】：∵ED∥BC，
∴∠EGB=∠GBC，∠DFC=∠FCB，
∵∠GBC=∠GBE，∠FCB=∠FCD，
∴∠EGB=∠EBG，∠DCF=∠DFC，
∴BE=EG，CD=DF，
∵FG=2，ED=6，
∴EB+CD=EG+DF=EF+FG+FG+DG=ED+FG=8，
故选C．
11.【答案】：B
【解析】：解：①BC=4cm，AC=5cm，∠ACB=30°，满足“SAS”，所以根据这组条件画图，△ABC唯一；
②BC=4cm，AC=3cm，∠ABC=30°，根据这组条件画图，△ABC可能为锐角三角形，也可为钝角三角形；
③BC=4cm，AC=5cm，∠ABC=90°；满足“HL”，所以根据这组条件画图，△ABC唯一；
④BC=4cm，AC=5cm，∠ABC=120°，根据这组条件画图，△ABC唯一．
所以，ΔABC不能够唯一确定的是②．
故选：B
12.【答案】：A
【解析】：解：∵∠B=90°，∠A=30°，AC=a，
∴BC=AC=a，
∵以点C为圆心，CB长为半径画弧交AC于点D，
∴CD=BC=a，
∵以点A为圆心，AD长为半径画弧交AB于点E，
∴AD=AE=AC-CD=a，
∵AB=m，
∴BE=AB-AE=m-a，
故选：A．
13.【答案】：D
【解析】：由题意得，∠ABD＝∠BAC，
A.在△ABC与△BAD中，
，
∴△ABC≌△BAD（SAS）；
故选项正确；
B.在△ABC与△BAD中，
，
△ABC≌△BAD（ASA），
故选项正确；
C.在△ABC与△BAD中，
，
△ABC≌△BAD（AAS），
故选项正确；
D.在△ABC与△BAD中，
BC＝AD，AB＝BA，∠BAC＝∠ABD（SSA），△ABC与△BAD不全等，故错误；
故选：D．
14.【答案】：C
【解析】：解：方程两边都乘以（x-3）得：
整理得：（m-2）x=2m-6，
由分式方程无解，
一种情况是未知数系数为0得：m-2=0，m=2，
一种情况是方程有增根得：x−3=0，即x=3，
把x=3代入整式方程得：m=0，
故选：C．
15.【答案】：A
【解析】：A
∵，
∵，
又∵甲与乙相乘得：，乙与丙相乘得：，
∴甲为，乙为，丙为，
∴甲、丙之积与乙的差是：
，
，
，
故选：A
16.【答案】：D
【解析】：解：A、∵AB=AC，BE⊥AC于E，CF⊥AB于F，∠A=∠A∴△ABE≌△ACF（AAS），正确；
B∵△ABE≌△ACF，AB=AC∴BF=CE，∠B=∠C，∠DFB=∠DEC=90°∴△BDF≌△CDE（ASA），正确；
C、∵△ABE≌△ACF，AB=AC∴BF=CE，∠B=∠C，∠DFB=∠DEC=90°∴DF=DE故点D在∠BAC的平分线上，正确；
D、无法判定，错误；
故选D．
【画龙点睛】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、SSA、HL． 注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．
二. 填空题
17.【答案】：
【解析】：解：
故答案为：．
18.【答案】： ④
【解析】：解：①，含因式；
②，含因式；
③，含因式；
④，不含因式；
故答案为：④．
19.【答案】： ①. ②.
【解析】：
=
=
=
=
故答案为：
三.解答题
20【答案】：
（1）；
（2）
【解析】：
解：（1）原式＝
；
（2）原式＝
．
21【答案】：
（1）
（2）无解
【解析】：
【小问1详解】
解：方程两边同乘以得，
解这个整式方程，得，
检验：将代入最简公式分母，
原分式方程的解为．
【小问2详解】
将方程两边同时乘以得：
，
解这个整式方程，得：，
将代入，
所以是增根，
所以原分式方程无解．
【画龙点睛】本题考查的是分式方程的求解，解题的关键是将分式方程转化为整式方程，易错点是漏乘不含未知数的项．
22【答案】：
（1）见解析；（2）、、；（3）2.5．
【解析】：
解：（1）如图，即是所作的图形；
（2），，
点A，B，C三点关于y轴对称点，，的坐标为：
、、；
（3）如图，
故答案为：．
．
23【答案】：
（1）∠EAC＝54°；
（2）．
【解析】：
【小问1详解】
∵∠EAD＝∠EDA，
∴∠EAC＋∠CAD＝∠B＋∠BAD，
∵AD平分∠BAC，
∴∠CAD＝∠BAD．
∴∠EAC＝∠B．
∵∠B＝54°，
∴∠EAC＝54°．
【小问2详解】
设∠CAD＝2x，则∠E＝5x，∠DAB＝2x，
∵∠B＝54°，
∴∠EDA＝∠EAD＝2x＋54°．
∵∠EDA＋∠EAD＋∠E＝180°，
∴2x＋54°＋2x＋54°＋5x＝180°．
解得x＝8°．
∴∠E＝5x＝40°．
24【答案】：
（1）
（2）
（3）5
【解析】：
【小问1详解】
解：，
【小问2详解】
解：，，
∴x+1＞0，x-5＞0，
，
；
【小问3详解】
解：，
，
∵，
∴，
∴a=1，，
．
25【答案】：
（1）水果店主购进第一批这种水果的单价是20元；（2）a的最大值是30．
【解析】：
（1）设第一批水果的单价是x元，
，
解得，x＝20，
经检验，x＝20是原分式方程的解，
答：水果店主购进第一批这种水果的单价是20元；
（2）由题意可得，
，
解得，a≤30，
答：a的最大值是30．
26【答案】：
（1）60，等边；（2）等边三角形，证明见解析（3）④.
【解析】：
（1）如图1，连接BD，
∵∠ABC=∠ADC=90°，∠MAN=120°，
根据四边形的内角和得，∠BCD=360°-（∠ABC+∠ADC+∠MAN）=60°，
∵AC是∠MAN的平分线，CD⊥AM．CB⊥AN，
∴CD=CB，（角平分线的性质定理），
∴△BCD是等边三角形；
故答案为60，等边；
（2）如图2，同（1）得出，∠BCD=60°（根据三角形的内角和定理），
过点C作CE⊥AM于E，CF⊥AN于F，
∵AC是∠MAN的平分线，
∴CE=CF，
∵∠ABC+∠ADC=180°，∠ADC+∠CDE=180°，
∴∠CDE=∠ABC，
在△CDE和△CFB中，
，
∴△CDE≌△CFB（AAS），
∴CD=CB，
∵∠BCD=60°，
∴△CBD是等边三角形；
（3）如图3，
∵OP平分∠EOF，∠EOF=120°，
∴∠POE=∠POF=60°，在OE上截取OG'=OP=1，连接PG'，
∴△G'OP是等边三角形，此时点H'和点O重合，
同理：△OPH是等边三角形，此时点G和点O重合，
将等边△PHG绕点P逆时针旋转到等边△PG'H'，在旋转的过程中，
边PG，PH分别和OE，OF相交（如图中G''，H''）和点P围成的三角形全部是等边三角形，（旋转角的范围为（0°到60°包括0°和60°），
所以有无数个；
理由：同（2）的方法．
故答案为④．