河北省巨鹿县2024-2025学年八年级（上）数学期末模拟测试（含答案及详解）

这是一份河北省巨鹿县2024-2025学年八年级（上）数学期末模拟测试（含答案及详解），共20页。试卷主要包含了选择题等内容，欢迎下载使用。
1. (-12)0 的值是（ ）
A B. C. 1D. 1
2. 下列运算正确的是（ ）
A. B.
C. D.
3. 熔喷布，俗称口罩的“心脏”，是口罩中间的过滤层，能过滤细菌，阻止病菌传播．经测量，医用外科口罩的熔喷布厚度约为0.000156米，将0.000156用科学记数法表示应为（ ）
A. B. C. D.
4. 等腰三角形的周长为13cm，其中一边长为3cm，则该等腰三角形的底边长为（ ）
A. 7cmB. 3cmC. 9cmD. 5cm
5. 如图，已知△ABC≌△DCB，∠A=75°，∠DBC=40°，则∠DCB的度数为（ ）
A. 75°B. 65°
C. 40°D. 30°
6. 若（x+m）（x﹣8）中不含x的一次项，则m的值为（ ）
A. 8B. ﹣8C. 0D. 8或﹣8
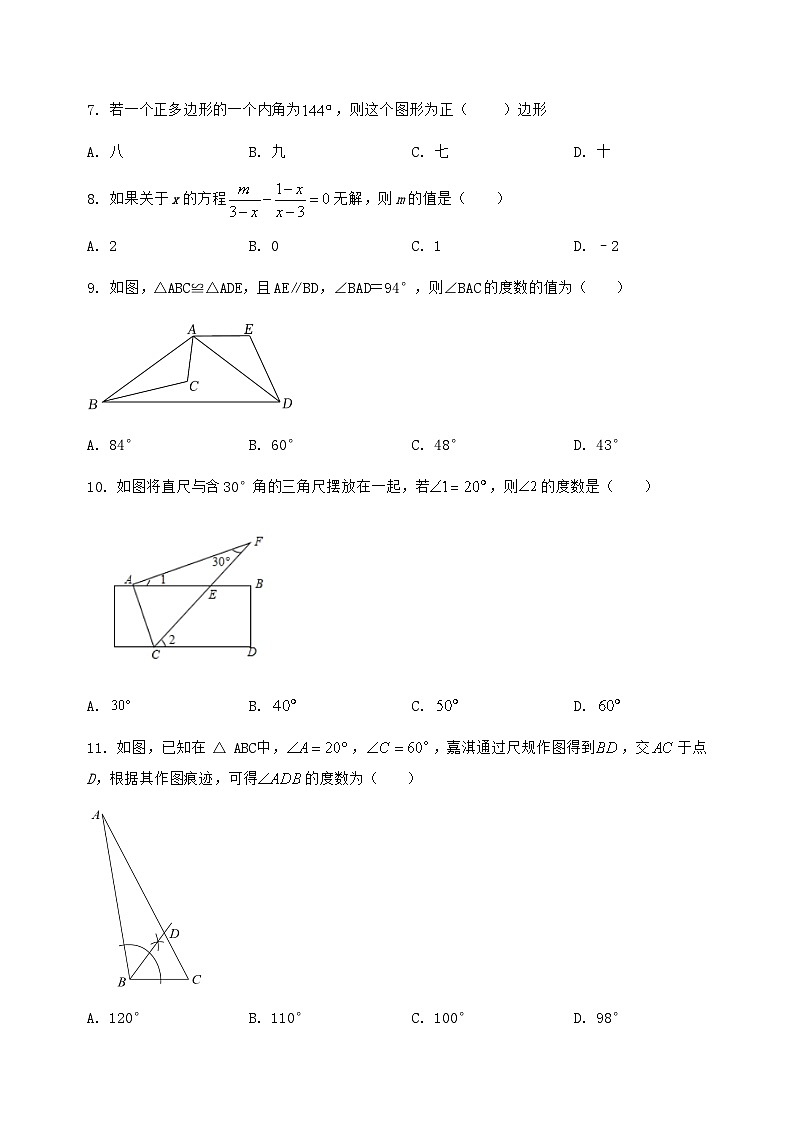
7. 若一个正多边形的一个内角为，则这个图形为正（ ）边形
A. 八B. 九C. 七D. 十
8. 如果关于x的方程无解，则m的值是（ ）
A. 2B. 0C. 1D. –2
9. 如图，△ABC≌△ADE，且AE∥BD，∠BAD＝94°，则∠BAC的度数的值为（ ）
A. 84°B. 60°C. 48°D. 43°
10. 如图将直尺与含30°角的三角尺摆放在一起，若，则的度数是（ ）
A. B. C. D.
11. 如图，已知在△ABC中，，，嘉淇通过尺规作图得到，交于点D，根据其作图痕迹，可得的度数为（ ）
A. 120°B. 110°C. 100°D. 98°
12. 若关于x的分式方程－2＝无解，则m的值为（ ）
A. 0B. 2C. 0或2D. 无法确定
13. 一个三角形两边长分别为4和6，且第三边长为整数，这样的三角形的周长最小值是（ ）
A. 20B. 16C. 13D. 12
14. 如图，在等边△ABC中，AD、CE是△ABC的两条中线，，P是AD上一个动点，则最小值的是（ ）
A. 2.5B. 5C. 7.5D. 10
15. 如图，已知点P是∠AOB角平分线上的一点，∠AOB=60°，PD⊥OA，M是OP的中点，DM=4cm，如果点C是OB上一个动点，则PC的最小值为( )
A. 2B. C. 4D.
16. 如图，在中，，，点，分别是，上的动点，将沿直线翻折，点的对点恰好落在边上，若是等腰三角形，那么的度数为（ ）
A. 或B. 或
C. ，或D. ，或
二.填空题(本大题共3题，总计 12分)
17. 计算： =_________．
18. 如图，△ABC中，是的垂直平分线，AE=3cm, △ABD的周长为，则的周长为______．
19. 如图，直线a∥b，点M、N分别为直线a和直线b上的点，连接MN，∠DMN=70°，点P是线段MN上一动点，直线DE始终经过点P，且与直线a、b分别交与点D、E，
（1）当△MPD与△NPE全等时，直接写出点P的位置：___________________；
（2）当△NPE是等腰三角形时，则∠NPE的度数为___________________．
三.解答题(共7题，总计66分，解答应写出文字说明、证明过程或演算步骤)
20. （1）因式分解：；
（2）化简：．
21. 先化简：，再从1，2，3中选取一个适当的数代入求值．
22. 如图，在下方单位长度为1的方格纸中画有一个△ABC．
（1）画出△ABC关于y轴对称△A′B′C′；
（2）求△ABC的面积．
23. 如图，在△ABC中，AB=AC，∠A=36°，DE是AB的垂直平分线．
（1）求证：△BCD是等腰三角形；
（2）若△ABD的周长是a，BC=b，求△BCD的周长．（用含a，b的代数式表示）
24. 【阅读】下列是多项式因式分解的过程：．请利用上述方法解决下列问题．
【应用】
（1）因式分解：；
（2）若x>5，试比较与0的大小关系；
（3）【灵活应用】若，求的值．
25. 为做好复工复产，某工厂用、两种型号机器人搬运原料，已知型机器人比型机器人每小时多搬运20千克，且型机器人搬运1200千克所用时间与型机器人搬运1000千克所用时间相等．
（1）求这两种机器人每小时分别搬运多少原料；
（2）为生产效率和生产安全考虑，，两种型号机器人都要参与原料运输但两种机器人不能同时进行工作，如果要求不超过5小时需完成对580千克原料的搬运，则型机器人至少要搬运多少千克原料？
26. 如图1，在长方形中，，点P从点B出发，以的速度沿向点C运动（点P运动到点C处时停止运动），设点P的运动时间为．
（1）_____________．（用含t的式子表示）
（2）当t何值时，△ABP≌△DCP？
（3）如图2，当点P从点B开始运动，同时，点Q从点C出发，以的速度沿向点D运动（点Q运动到点D处时停止运动，两点中有一点停止运动后另一点也停止运动），是否存在这样的值使得与全等？若存在，请求出的值；若不存在，请说明理由．
巨鹿县2024-2025学年八年级（上）数学期末模拟测试
参考答案及解析
一.选择题
1.【答案】：C
【解析】：解：
故选C
2.【答案】：D
【解析】：A、，故不符合题意；
B 、，故不符合题意；
C、，故不符合题意；
D、，故符合题意；
故选：D．
3.【答案】：C
【解析】：解：0.000156用科学记数法可表示为1.56×10﹣4．
故选：C．
4.【答案】：B
【解析】：当长是3cm的边是底边时，三边为3cm，5cm，5cm，等腰三角形成立；
当长是3cm的边是腰时，底边长是：13﹣3﹣3=7（cm），而3+3＜7，不满足三角形的三边关系．
故底边长：3cm．
故选：B．
5.【答案】：B
【解析】：解：∵△ABC≌△DCB，
∴∠D=∠A=75°，∠ACB=∠DBC=40°，
∴∠DCB=180°-75°-40°=65°，
故选：B．
6.【答案】：A
【解析】：原式，
由结果不含一次项，得到，即，
则的值为8，
故选：A．
7.【答案】：D
【解析】：解：设所求正n边形边数为n， 则
解得
故答案为：D．
8.【答案】：A
【解析】：解：方程去分母得：m+1﹣x=0，
解得x=m+1，
当分式方程分母为0，即x=3时，方程无解，
则m+1=3，
解得m=2.
故选A.
9.【答案】：D
【解析】：∵△ABC≌△ADE，∠BAD＝94°，
∴AB＝AD，∠BAC＝∠DAE，
∴∠ABD＝∠ADB＝×（180°﹣94°）＝43°，
∵AE//BD，
∴∠DAE＝∠ADB＝43°，
∴∠BAC＝∠DAE＝43°．
故选：D．
10.【答案】：C
【解析】：如图，
∵∠BEF是△AEF的外角，∠1=20，∠F=30，
∴∠BEF=∠1+∠F=50，
∵AB∥CD，
∴∠2=∠BEF=50，
故选：C．
11.【答案】：B
【解析】：根据作图痕迹可知，是∠ABC的平分线，
∵，，
∴
∵是∠ABC的平分线，
∴
∴
故选：B．
12.【答案】：C
【解析】：解：方程两边都乘以（x-3）得：
整理得：（m-2）x=2m-6，
由分式方程无解，
一种情况是未知数系数为0得：m-2=0，m=2，
一种情况是方程有增根得：x−3=0，即x=3，
把x=3代入整式方程得：m=0，
故选：C．
13.【答案】：C
【解析】：解：设三角形的第三边为x，
∵三角形的两边长分别为4和6，
∴2＜x＜10，
∵第三边为整数，
∴第三边x的最小值为3，
∴三角形周长的最小值为：3+4+6=13．
故选：C
14.【答案】：B
【解析】：解：连结PC，
∵△ABC为等边三角形，
∴AB=AC，
∵AD为中线，
∴AD⊥BC，BD=CD=，
∵点P在AD上，BP=CP，
∴PE+PB=PE+PC，
∵PE+PC≥CE
∴C、P、E三点共线时PE+CP最短=CE，
∵CE为△ABC的中线，
∴CE⊥AB，AE=BE=，
∵△ABC为等边三角形，
∴AB=BC，∠ABC=60°，
∴BE=BD，
在△ABD和△CBE中，
，
∴△ABD≌△CBE（SAS）
∴AD=CE=5，
∴PB+PE的最小值为5．
故选择B．
15.【答案】：C
【解析】：解：∵P是∠AOB角平分线上的一点，∠AOB=60°，
∴∠AOP=∠AOB=30°，
∵PD⊥OA，M是OP的中点，DM=4cm，
∴OP=2DM=8，
∴PD=OP=4，
∵点C是OB上一个动点，
∴PC的最小值为P到OB距离，
∴PC的最小值=PD=4．
故选C
16.【答案】：D
【解析】：，，
，
分三种情况讨论：
①当时，如图：
，
；
②当时，如图：
，
；
③当时，如图：
，
；
综上所述，为或或，
故选：D．
二. 填空题
17.【答案】： 3
【解析】：原式=1+2=3
故答案为：3．
18.【答案】： 19cm
【解析】：解：∵是的垂直平分线，
∴cm，，
∴AC＝AE＋CE＝6（cm），
∵的周长为，
∴（cm），
∴（cm），即（cm），
∴（cm）；
∴△ABC的周长为19cm；
故答案为：19cm．
19.【答案】： ①. MN中点处 ②. 70°或40°或55°
【解析】：（1）∵a//b
∴∠DMN=∠PNE，∠MDE=∠DEN，
∴当△MPD与△NPE全等时，即△MPD≌△NPE时MP=NP，
即点P是MN的中点．
故答案为：MN中点处
（2）①若PN=PE时，
∵∠DMN=∠PNE=70°，
∴∠DMN =∠PNE=∠PEN=70°．
∴∠NPE=180°-∠PNE-∠PEN=180°-70°-70°=40°．
∴∠NPE =40°；
②若EP=EN时，则∠NPE =∠PNE=∠DMN =70°；
③若NP=NE时，则∠PEN=∠NPE，此时2∠NPE=180°-∠PNE=180°-∠DMN =180°-70°=110°
∴∠NPE =55°；
综上所述，∠NPE的值是40°或70°或55°．
故答案为：40°或70°或55°．
三.解答题
20【答案】：
（1）；
（2）
【解析】：
解：（1）原式＝
；
（2）原式＝
．
21【答案】：
，-5.
【解析】：
原式
，
当，2时分式无意义，
将，代入原式得：
则原式．
22【答案】：
（1）见解析；（2）
【解析】：
（1）解：△ABC关于y轴对称的如下图所示 ：
（2）
．
23【答案】：
（1）见解析 （2）a﹣b
【解析】：
【小问1详解】
证明：∵AB=AC，∠A=36°，
∴∠ABC=∠C==72°，
∵DE是AC的垂直平分线，
∴AD=BD，
∴∠ABD=∠A=36°，
∵∠CDB是△ADB的外角，
∴∠CDB=∠ABD+∠A=72°，
∴∠C=∠CDB，
∴CB=DB，
∴△BCD是等腰三角形；
【小问2详解】
解：由（1）可知AD=BD=CB=b，
∵△ABD周长是a，
∴AB=a﹣2b，
∵AB=AC，
∴CD=a﹣3b，
∴△BCD的周长=CD+BD+BC=a﹣3b+b+b=a﹣b．
【画龙点睛】本题考查了等腰三角形的性质与判定，线段垂直平分线的性质，三角形的内角和与三角形的外角的定义与性质，综合运用以上知识是解题的关键．
24【答案】：
（1）
（2）
（3）5
【解析】：
【小问1详解】
解：，
【小问2详解】
解：，，
∴x+1＞0，x-5＞0，
，
；
【小问3详解】
解：，
，
∵，
∴，
∴a=1，，
．
25【答案】：
（1）型机器人每小时搬运120千克原料，型机器人每小时搬运100千克原料；
（2）型机器人至少要搬运480千克原料．
【解析】：
（1）解：设型机器人每小时搬运千克原料
解得：
经检验，是原方程的解
∴．
答：A型机器人每小时搬运120千克原料，型机器人每小时搬运100千克原料．
（2）设A型机器人要搬运千克原料.

解得：
答：A型机器人至少要搬运480千克原料．
26【答案】：
（1）；（2）；（3）存在，或，理由见解析．
【解析】：
解：（1）由题意得，，
∴PC=BC-BP=10-2t，
故答案为：；
（2）若△ABP≌△DCP
则
∴2t=10-2t
即
当时，△ABP≌△DCP；
（3）存在，理由如下：
当时，△ABP≅△PCQ
∴2t=4
∴v=2；
当时，△ABP≅△QCP
∴2t=5
∴2.5v=6
∴v=2.4
综上所述，当或时，与全等．