人教版数学九上期末模拟预测卷02（2份，原卷版+解析版）

这是一份人教版数学九上期末模拟预测卷02（2份，原卷版+解析版），文件包含人教版数学九上期末模拟预测卷02原卷版doc、人教版数学九上期末模拟预测卷02解析版doc等2份试卷配套教学资源，其中试卷共31页， 欢迎下载使用。

（考试时间：100分钟 试卷满分：120分）
考生注意：
本试卷26道试题，满分120分，考试时间100分钟．
本试卷分设试卷和答题纸．试卷包括试题与答题要求．作答必须涂（选择题）或写（非选择题）在答题纸上，在试卷上作答一律不得分．
答卷前，务必用钢笔或圆珠笔在答题纸正面清楚地填写姓名、准考证号码等相关信息．
一．选择题（共10小题每题3分，满分30分）
1．一元二次方程2x2+x﹣1＝0的二次项系数为（ ）
A．﹣1B．0C．1D．2
【分析】根据一元二次方程的一般形式得出选项即可．
【解答】解：一元二次方程2x2+x﹣1＝0的二次项系数为2，
故选：D．
【点评】本题考查了一元二次方程的一般形式，能熟记一元二次方程的一般形式是解此题的关键，一元二次方程的一般形式是ax2+bx+c＝0（a、b、c为常数，a≠0）．
2．如图所示的几何体的主视图是（ ）
A．B．C．D．
【分析】找到从几何体的正面看所得到的图形即可．
【解答】解：主视图是一个“L”形的组合图形．
故选：A．
【点评】此题主要考查了简单几何体的三视图，主视图是从物体的正面看得到的视图．
3．小明用一面放大镜观察一个三角形，则这个三角形没有发生变化的是（ ）
A．三角形的边长B．三角形的各内角度数
C．三角形的面积D．三角形的周长
【分析】根据相似三角形的性质解答即可．
【解答】解：∵小明用一面放大镜观察一个三角形，
∴看到的三角形和原三角形相似，
∴这个三角形没有发生变化的是三角形的各内角度数，
故选：B．
【点评】本题考查了相似图形，熟练掌握相似图形的性质是解题的关键．
4．2021年的“一圈两场三改”工作标志着贵阳市民生建设迈入新阶段，某区11月开放体育场馆30所，预计到2022年1月开放体育场馆达63所，若设每个月开放体育场馆的平均增长率为x，则所列的方程为（ ）
A．30（1+x）＝63B．30（1+x）2＝63
C．30（1﹣x）＝63D．30（l﹣x）2＝63
【分析】利用2022年1月开放体育馆数量＝2021年11月开放体育馆数量×（1+每个月开放体育场馆的平均增长率）2，即可得出关于x的一元二次方程，此题得解．
【解答】解：依题意得：30（1+x）2＝63．
故选：B．
【点评】本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方程是解题的关键．
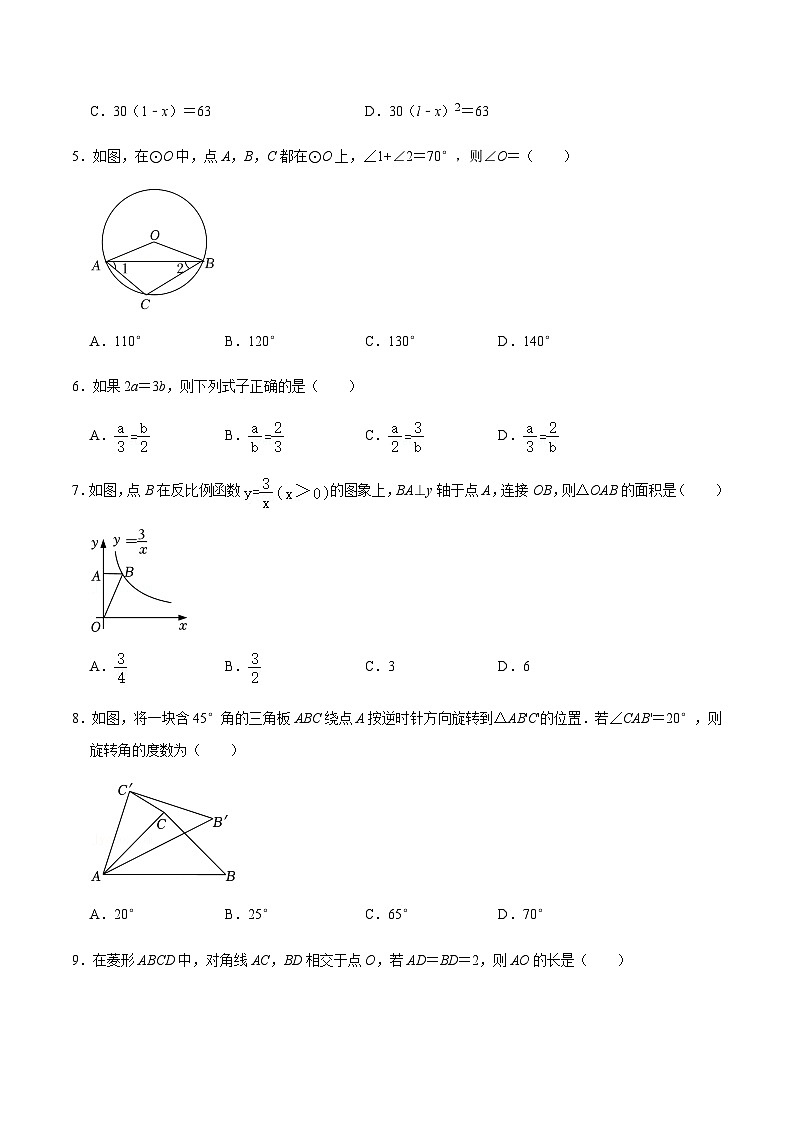
5．如图，在⊙O中，点A，B，C都在⊙O上，∠1+∠2＝70°，则∠O＝（ ）
A．110°B．120°C．130°D．140°
【分析】由三角形内角和定理求出∠C＝110°，由圆内接四边形的性质求出∠D＝70°，则可求出答案．
【解答】解：如图，在优弧AB上取点D，连接AD，BD，
∵∠1+∠2＝70°，
∴∠C＝110°，
∵四边形ACBD内接于圆，
∴∠C+∠D＝180°，
∴∠D＝70°，
∴∠O＝2∠D＝140°．
故选：D．
【点评】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半，也考查了圆内接四边形的性质及三角形内角和定理．
6．如果2a＝3b，则下列式子正确的是（ ）
A．B．C．D．
【分析】把每一个选项的比例式转化为等积式，逐一判断即可解答．
【解答】解：A、∵＝，
∴2a＝3b，
故A符合题意；
B、∵＝，
∴3a＝2b，
故B不符合题意；
C、∵＝，
∴ab＝6，
故C不符合题意；
D、∵＝，
∴ab＝6，
故D不符合题意；
故选：A．
【点评】本题考查了比例的性质，熟练掌握比例的性质是解题的关键．
7．如图，点B在反比例函数的图象上，BA⊥y轴于点A，连接OB，则△OAB的面积是（ ）
A．B．C．3D．6
【分析】根据反比例函数系数k的几何意义，即可确定△OAB的面积．
【解答】解：∵点B在反比例函数的图象上，BA⊥y轴于点A，
∴△OAB的面积为，
故选：B．
【点评】本题考查了反比例函数系数k的几何意义，熟练掌握反比例函数系数k的几何意义是解题的关键．
8．如图，将一块含45°角的三角板ABC绕点A按逆时针方向旋转到△AB'C'的位置．若∠CAB'＝20°，则旋转角的度数为（ ）
A．20°B．25°C．65°D．70°
【分析】根据旋转的性质得出∠BAC＝∠B'AC'＝45°，再根据∠CAB'＝20°，即可求解．
【解答】解：∵将一块含45°角的三角板ABC绕点A按逆时针方向旋转到△AB'C'的位置．
∴∠BAC＝∠B'AC'＝45°，
∵∠CAB'＝20°，
∴旋转角BAB'＝∠BAC﹣∠CAB'＝45°﹣20°＝25°，
故选：B．
【点评】本题考查了旋转的性质，正确确定旋转角是解题的关键．
9．在菱形ABCD中，对角线AC，BD相交于点O，若AD＝BD＝2，则AO的长是（ ）
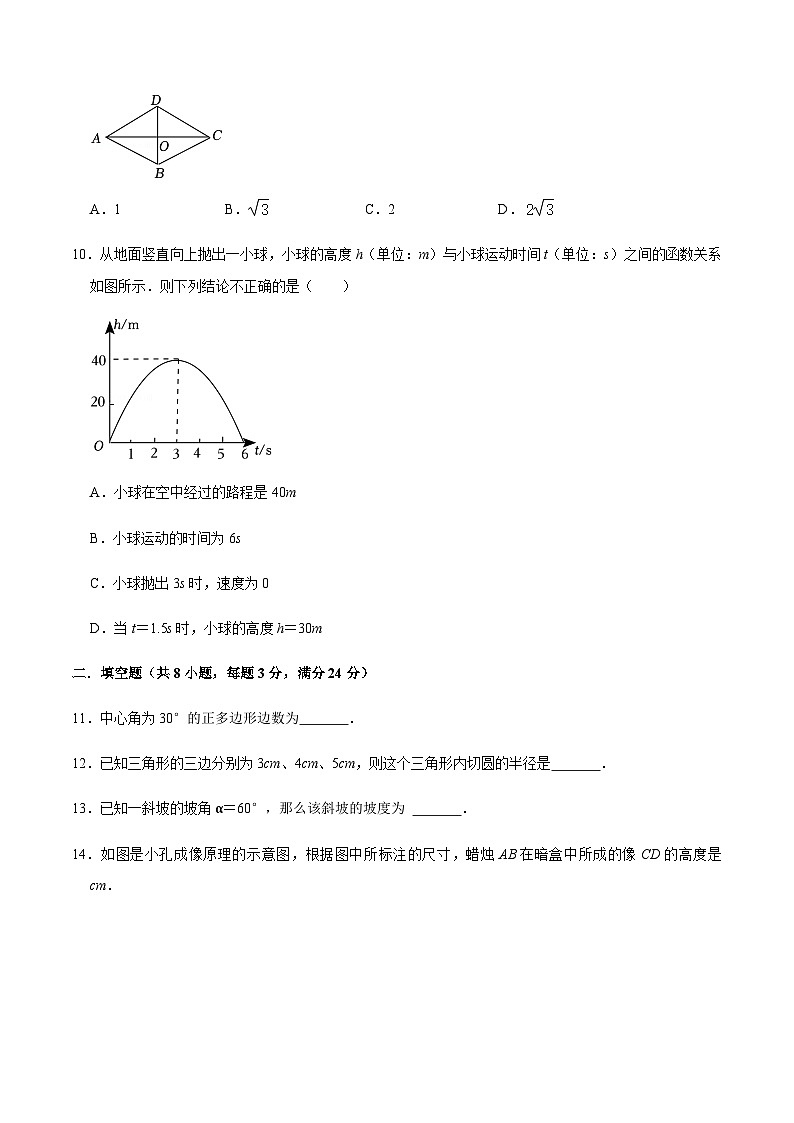
A．1B．C．2D．
【分析】由菱形的性质可得AC⊥BD，AB＝AD＝BD＝2，由直角三角形的性质即可求解．
【解答】解：∵四边形ABCD是菱形，AD＝BD＝2
∴AC⊥BD，AB＝AD＝2，DO＝BO＝1，
在Rt△AOD中，
AO＝＝．
故选：B．
【点评】本题考查了菱形的性质，掌握菱形的对角线互相垂直平分是解题的关键．
10．从地面竖直向上抛出一小球，小球的高度h（单位：m）与小球运动时间t（单位：s）之间的函数关系如图所示．则下列结论不正确的是（ ）
A．小球在空中经过的路程是40m
B．小球运动的时间为6s
C．小球抛出3s时，速度为0
D．当t＝1.5s时，小球的高度h＝30m
【分析】根据二次函数图象和性质求解．
【解答】解：A：由图象知小球在空中经过的路程是40×2＝80m；故A是错误的；
B：当t＝6时，高度为0，则运动时间是6s，或由图象可知，小球6s时落地，故小球运动的时间为6s，故B是正确的；
C：小球抛出3秒时达到最高点，即速度为0，故C是正确的；
D：设函数解析式为：h＝a（t﹣3）2+40，
由题意得：a（0﹣3）2+40＝0，
解得：a＝﹣，
∴h＝﹣（t﹣3）2+40，
当t＝1.5时，h＝﹣×（1.5﹣3）2+40＝30，，故D是正确的；
故选：A．
【点评】本题考查了二次函数图象应用，待定系数法求函数解析式和数形结合思想是解题的关键．
二．填空题（共8小题，每题4分，满分24分）
11．中心角为30°的正多边形边数为 12 ．
【分析】根据正n边形的中心角的度数为360°÷n进行计算即可得到答案．
【解答】解：因为360°÷30°＝12．
所以这个正多边形的边数为12．
故答案为：12．
【点评】本题考查的是正多边形内角、外角和中心角的知识，掌握中心角的计算公式是解题的关键．
12．已知三角形的三边分别为3cm、4cm、5cm，则这个三角形内切圆的半径是 1 ．
【分析】先利用勾股定理的逆定理证明这个三角形为直角三角形，然后利用直角边为a、b，斜边为c的三角形的内切圆半径为求解．
【解答】解：∵32+42＝52，
∴这个三角形为直角三角形，
∴这个三角形内切圆的半径＝＝1．
故答案为1．
【点评】本题考查了三角形的内切圆与内心：与三角形各边都相切的圆叫三角形的内切圆，三角形的内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形．三角形的内心就是三角形三个内角角平分线的交点．记住直角边为a、b，斜边为c的三角形的内切圆半径为．
13．已知一斜坡的坡角α＝60°，那么该斜坡的坡度为 ．
【分析】由于斜坡的坡角为60°，而坡度为坡角的正切，由此即可确定个斜坡的坡度i．
【解答】解：∵斜坡的坡角为60°，
∴这个斜坡的坡度i＝tan60°＝．
故答案为：．
【点评】此题主要考查了解直角三角形应用﹣坡度坡角的问题，解题的关键是利用三角函数解决问题．
14．如图是小孔成像原理的示意图，根据图中所标注的尺寸，蜡烛AB在暗盒中所成的像CD的高度是 1 cm．
【分析】正确理解小孔成像的原理，利用相似三角形的判定得出△ABO∽△CDO，结合相似三角形的性质，利用AB的值求出DC．
【解答】解：由题意可得：AB∥DC，
则△ABO∽△CDO，
故＝＝，
解得：DC＝1（cm）．
故答案为：1．
【点评】此题主要考查了相似三角形的应用，相似比等于对应高之比在相似中用得比较广泛．
15．发射一枚炮弹，经x秒后的高度为y米，且时间与高度的关系为y＝ax2+bx+c（a≠0）．若此炮弹在第7秒与第15秒时的高度相等，则第 11 秒时炮弹位置达到最高．
【分析】求出抛物线的对称轴，即可得炮弹位置达到最高时x的值．
【解答】解：∵此炮弹在第7秒与第15秒时的高度相等，
∴抛物线的对称轴是直线x＝＝11，
∴炮弹位置达到最高时，时间是第11秒．
故答案为：11．
【点评】本题考查二次函数的应用，解题的关键是求出抛物线的对称轴．
16．如图，在Rt△ABC中，∠C＝90°，AC＝8，BC＝6．若以AC所在直线为轴，把△ABC旋转一周，得到一个圆锥，则这个圆锥的侧面积等于 60π ．
【分析】运用公式s＝πlr（其中勾股定理求解得到的母线长l为5）求解．
【解答】解：由已知得，母线长AB＝10，半径r为6，
∴圆锥的侧面积是s＝πlr＝10×6×π＝60π．
故答案为60π．
【点评】本题考查了圆锥的计算，要学会灵活的运用公式求解．
17．如图，四边形ABCD内接于⊙O，点M在AD的延长线上，∠AOC＝140°，则∠CDM＝ 70° ．
【分析】根据圆周角定理得到∠B＝70°，再根据圆内接四边形的任意一个外角等于它的内对角即可得解．
【解答】解：∵∠AOC＝140°，
∴∠B＝∠AOC＝70°，
∵四边形ABCD内接于⊙O，
∴∠CDM＝∠B＝70°，
故答案为：70°．
【点评】此题考查了圆内接四边形的性质、圆周角定理，熟记圆内接四边形的性质、圆周角定理是解题的关键．
18．已知抛物线y＝ax2﹣4ax+c（a≠0）与x轴交于A、B两点，若点A的坐标为（﹣2，0），则线段AB的长为 8 ．
【分析】将点A的坐标代入抛物线解析式可求得c＝﹣12a，再令y＝0，可求得点B的坐标，即可求得答案．
【解答】解：把A（﹣2，0）代入y＝ax2﹣4ax+c，得：4a+8a+c＝0，
解得：c＝﹣12a，
∴y＝ax2﹣4ax﹣12a，
令y＝0，得ax2﹣4ax﹣12a＝0，
∵a≠0，
∴x2﹣4x﹣12＝0，
解得：x1＝﹣2，x2＝6，
∴A（﹣2，0），B（6，0），
∴AB＝6﹣（﹣2）＝8，
故答案为：8．
【点评】本题考查了二次函数与一元二次方程的关系，待定系数法，二次函数图象与x轴的交点等，利用二次函数与一元二次方程的关系求点B的坐标是解题关键．
三．解答题（共8小题，满分66分）
19．计算：（﹣）﹣1++2cs60°﹣（π﹣1）0．
【分析】先化简各项，再作加减法，即可计算．
【解答】解：原式＝
＝0，
故答案为：0．
【点评】此题考查实数的混合运算以及特殊角的三角函数值，关键是掌握运算法则和运算顺序．
20．如图，在直角坐标平面内，已知点A（8，0），点B（3，0），点C是点A关于点B的对称点．
（1）求点C的坐标；
（2）若P坐标为（0，2），过点P作直线l∥x轴，点A关于直线l的对称点是D，求△BCD的面积．
【分析】（1）由A、B坐标得出AB＝5，根据点C是点A关于点B的对称点知BC＝AB＝5，据此可得；
（2）求得AD和BC得到长，然后利用三角形面积公式即可求得．
【解答】解：（1）∵点A（8，0），点B（3，0），
∴AB＝5，
∵点C是点A关于点B的对称点，
∴BC＝AB，
则点C的坐标为（﹣2，0）；
（2）∵AB＝5，P坐标为（0，2），
∴BC＝AB＝5，AD＝4，
∴S△BCD＝BC•AD＝＝10．
【点评】本题主要考查坐标与图形的变化﹣对称，解题的关键是掌握对称的定义和性质．
21．为铸牢中华民族共同体意识，不断巩固民族大团结，红星中学即将举办庆祝建党100周年“中华民族一家亲，同心共筑中国梦”主题活动，学校拟定了演讲比赛、文艺汇演、书画展览、知识竞赛四种活动方案，为了解学生对活动方案的喜爱情况，学校随机抽取了200名学生进行调查（每人只能选择一种方案），将调查结果绘制成如下两幅不完整的统计图，请你根据以下两幅图所给的信息解答下列问题．
（1）在抽取的200名学生中，选择“演讲比赛”的人数为 40 ，在扇形统计图中，m的值为 30 ；
（2）根据本次调查结果，估计全校2000名学生中选择“文艺汇演”的学生大约有多少人？
（3）现从喜爱“知识竞赛”的四名同学a、b、c、d中，任选两名同学参加学校知识竞赛，请用树状图或列表法求出a同学参加的概率．
【分析】（1）总人数乘以A对应的百分比即可求出其人数，再根据四种方案的人数之和等于总人数求出C方案人数，再用C方案人数除以总人数即可得出m的值；
（2）总人数乘以样本中B方案人数所占比例；
（3）列表得出所有等可能结果，从中找到符合条件的结果数，再根据概率公式求解即可．
【解答】解：（1）在抽取的200名学生中，选择“演讲比赛”的人数为：200×20%＝40（人），
则选择“书画展览”的人数为200﹣（40+80+20）＝60（人），
∴在扇形统计图中，m%＝×100%＝30%，即m＝30，
故答案为：40，30；
（2）估计全校2000名学生中选择“文艺汇演”的学生大约有2000×＝800（人）；
（3）列表如下：
由表可知，共有12种等可能结果，其中a同学参加的有6种结果，
所以a同学参加的概率为＝．
【点评】本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果n，再从中选出符合事件A或B的结果数目m，然后利用概率公式计算事件A或事件B的概率．也考查了统计图．
22．已知：如图，在菱形ABCD中，对角线AC、BD相交于点O，DE∥AC，AE∥BD．
（1）求证：四边形AODE是矩形；
（2）若AB＝6，∠ABC＝60°，求四边形AODE的面积．
【分析】（1）先证四边形AODE为平行四边形，再由菱形的性质得∠AOD＝90°，即可得出结论；
（2）证△ABC是等边三角形，得出AC＝AB＝6，则OA＝3，再由勾股定理得出OD的长，即可求解．
【解答】（1）证明：∵DE∥AC，AE∥BD，
∴四边形AODE是平行四边形，
∵四边形ABCD是菱形，
∴AC⊥BD，
∴∠AOD＝90°，
∴平行四边形AODE是矩形；
（2）解：∵四边形ABCD是菱形，
∴AD＝AB＝BC＝6，OA＝OC，AC⊥BD，
∵∠ABC＝60°，
∴△ABC是等边三角形，
∴AC＝AB＝6，
∴OA＝AC＝3，
在Rt△AOD中，由勾股定理得：OD＝＝＝3，
由（1）得：四边形AODE是矩形，
∴四边形AODE的面积＝OA•OD＝3×3＝9．
【点评】本题考查了矩形的判定与性质、菱形的性质、平行四边形的判定与性质、等边三角形的判定与性质、勾股定理等知识，熟练掌握矩形的判定与性质是解题的关键．
23．某社区为了更好地开展“垃圾分类，美丽宁波”活动，需购买A，B两种类型垃圾桶，用1600元可购进A型垃圾桶14个和B型垃圾桶8个，且购买3个A型垃圾桶的费用与购买4个B型垃圾桶的费用相同，请解答下列问题：
（1）求出A型垃圾桶和B型垃圾桶的单价．
（2）若社区欲用不超过3600元购进两种垃圾桶共50个，其中A型垃圾桶至少29个，求有哪几种购买方案？
【分析】（1）设A型垃圾桶的单价为x元，B型垃圾桶的单价为y元，根据“用1600元可购进A型垃圾桶14个和B型垃圾桶8个，且购买3个A型垃圾桶的费用与购买4个B型垃圾桶的费用相同”，即可得出关于x，y的二元一次方程组，解之即可得出A型垃圾桶和B型垃圾桶的单价；
（2）设购进A型垃圾桶m个，则购进B型垃圾桶（50﹣m）个，根据“A型垃圾桶至少购进29个，且购进50个垃圾桶的总费用不超过3600元”，即可得出关于m的一元一次不等式组，解之即可得出m的取值范围，再结合m为正整数，即可得出各购买方案．
【解答】解：（1）设A型垃圾桶的单价为x元，B型垃圾桶的单价为y元，
依题意得：，
解得：．
答：A型垃圾桶的单价为80元，B型垃圾桶的单价为60元．
（2）设购进A型垃圾桶m个，则购进B型垃圾桶（50﹣m）个，
依题意得：，
解得：29≤m≤30．
又∵m为正整数，
∴m可以取29，30，
∴该社区共有2种购买方案，
方案1：购进A型垃圾桶29个，B型垃圾桶21个；
方案2：购进A型垃圾桶30个，B型垃圾桶20个．
【点评】本题考查了二元一次方程组的应用以及一元一次不等式组的应用，解题的关键是：（1）找准等量关系，正确列出二元一次方程组；（2）根据各数量之间的关系，正确列出一元一次不等式组．
24．如图，在Rt△ABC中，∠ACB＝90°，AO是△ABC的角平分线．以O为圆心，OC为半径作⊙O．
（1）求证：AB是⊙O的切线．
（2）已知AO交⊙O于点E，延长AO交⊙O于点D，tan∠D＝，求的值．
（3）在（2）的条件下，设⊙O的半径为3，求AB的长．
【分析】（1）由于题目没有说明直线AB与⊙O有交点，所以过点O作OF⊥AB于点F，然后证明OC＝OF即可；
（2）连接CE，先求证∠ACE＝∠ODC，然后可知△ACE∽△ADC，所以＝，而tan∠D＝于是得到结论；
（3）由（2）可知，AC2＝AE•AD，所以可求出AE和AC的长度，由（1）可知，△OFB∽△ABC，所以＝，然后利用勾股定理即可求得AB的长度．
【解答】解：（1）如图，过点O作OF⊥AB于点F，
∵AO平分∠CAB，
OC⊥AC，OF⊥AB，
∴OC＝OF，
∴AB是⊙O的切线；
（2）如图，连接CE，
∵ED是⊙O的直径，
∴∠ECD＝90°，
∴∠ECO+∠OCD＝90°，
∵∠ACB＝90°，
∴∠ACE+∠ECO＝90°，
∴∠ACE＝∠OCD，
∵OC＝OD，
∴∠OCD＝∠ODC，
∴∠ACE＝∠ODC，
∵∠CAE＝∠CAE，
∴△ACE∽△ADC，
∴＝＝，
∴∠ACE+∠ECO＝90°，
∵tan∠D＝，
∴＝，
∴＝；
（3）由（2）可知：＝，
∴设AE＝x，AC＝2x，
∵△ACE∽△ADC，
∴＝，
∴AC2＝AE•AD，
∴（2x）2＝x（x+6），
解得：x＝2或x＝0（不合题意，舍去），
∴AE＝2，AC＝4，
由（1）可知：AC＝AF＝4，
∠OFB＝∠ACB＝90°，
∵∠B＝∠B，
∴△OFB∽△ACB，
∴＝，
设BF＝a，
∴BC＝，
∴BO＝BC﹣OC＝﹣3，
在Rt△BOF中，
BO2＝OF2+BF2，
∴（﹣3）2＝32+a2，
解得：a＝或a＝0（不合题意，舍去），
∴AB＝AF+BF＝．
【点评】本题考查圆的综合问题，解题的关键是证明△ACE∽△ADC．本题涉及勾股定理，解方程，圆的切线判定知识，内容比较综合，需要学生构造辅助线才能解决问题，对学生综合能力要求较高．
25．我们规定，对于已知线段AB，若存在动点C（点C不与点A，B重合）始终满足∠ACB的大小为定值，则称△ABC是“立信三角形”，其中AB的长称为它的“立信长”，∠ACB称为它的“立信角”．
（1）如图（1），已知立信△ABC中“立信长”AB＝2，“立信角”∠ACB＝90°，请直接写出立信△ABC面积的最大值；
（2）如图（2），在△ABD中，AD＝BD＝2，，C是立信△ABC所在平面上的一个动点，且立信角∠ACB＝60°，求立信△ABC面积的最大值；
（3）如图（3），已知立信长AB＝a（a是常数且a＞0），点C是平面内一动点且满足立信角∠ACB＝120°，若∠ABC，∠BAC的平分线交于点D，问：点D的运动轨迹长度是否为定值？如果是，请求出它的轨迹长度；如果不是，请说明理由．
【分析】（1）如图1中，取AB的中点T，连接CT，过点C作CH⊥AB于点H．利用垂线段最短解决问题即可；
（2）如图2中，过点D作DH⊥AB于点H，判断出点C在D为圆心，DA为半径的圆上运动，当点C运动到C′时，△ACB的面积最大，此时C′，D，H共线；
（3）利用弧长公式计算，求出圆心角，半径即可解决问题．
【解答】解：（1）如图1中，取AB的中点T，连接CT，过点C作CH⊥AB于点H．
∵∠ACB＝90°，AT＝TB，AB＝2，
∴CT＝AB＝1，
∴S△ACB＝×AB×CH≤×AB×CT＝1，
∴△ACB的面积的最大值为1；
（2）如图2中，过点D作DH⊥AB于点H，
∵DA＝DB＝2，DH⊥AB，AB＝2，
∴AH＝HB＝，
∴cs∠DAB＝，
∴∠DAB＝∠DBA＝30°，
∴∠ADB＝180°﹣30°﹣30°＝120°，DH＝AD＝1，
∵∠ACB＝60°，
∴∠ACB＝∠ADB，
∴点C在D为圆心，DA为半径的圆上运动，
当点C运动到C′时，△ACB的面积最大，此时C′，D，H共线，
∴△ACB的面积的最大值＝×2×3＝3；
（3）点D的运动轨迹长度为定值，理由如下：
如图3中，以AB为边向下作等边△AOB，以O为圆心，OA为半径作⊙O，在⊙O上AB三点下方取一点K，连接AK，BK．
∵∠ACB＝120°，AD平分∠CAB，BD平分∠ABC，
∴∠ADB＝150°，
∵∠K＝∠AOB＝30°，
∴∠K+∠ADB＝180°，
∴A，K，B，D四点共圆，
∴点D的运动轨迹是，
∴点D的运动轨迹长度为定值，运动路径的长＝＝，
当点C在AB的下方时，同法可得点D的运动轨迹为，
综上所述，点D运动轨迹的长为．
【点评】本题属于三角形综合题，考查了三角形的面积，弧长公式，解直角三角形，轨迹等知识，解题的关键是正确寻找点的运动轨迹，属于中考压轴题．
26．如图，已知抛物线经过A（﹣1，0），B（3，0），C（0，3）三点．
（1）求抛物线的解析式；
（2）连接BC，点D是线段BC上方抛物线上一点，过点D作DE∥BC，交x轴于点E，连接AD交BC于点F，当取得最小值时，求点D的横坐标；
（3）点G为抛物线的顶点，抛物线对称轴与x轴交于点H，连接GB，点M是抛物线上的动点，设点M的横坐标为m．
①当∠MBA＝∠BGH时，求点M的坐标；
②过点M作MN∥x轴，与抛物线交于点N，P为x轴上一点，连接PM，PN，将△PMN沿着MN翻折，得△QMN，若四边形MPNQ恰好为正方形，求m的值．
【分析】（1）用待定系数法求函数的解析式；
（2）由平行线可得＝，当AE有最大值时有最小值，设D（t，﹣t2+2t+3），过D点的直线DE的解析式为y＝﹣x﹣t2+3t+3，则＝，当t＝时，有最小值；
（3）①由tan∠BGH＝tan∠MBA＝，过点M作MK⊥x轴交于K点，则＝，所以|3﹣m|＝2|﹣m2+2m+3|，求出m＝﹣或m＝﹣，即可求M（﹣，）或（﹣，﹣）；
②根据正方形的对称性可知P、Q的横坐标为1，再由M（m，﹣m2+2m+3），求出N（2﹣m，﹣m2+2m+3），可得|1﹣m|＝|﹣m2+2m+3|，解得m＝或m＝．
【解答】解：（1）设y＝ax2+bx+c，
将A（﹣1，0），B（3，0），C（0，3）代入y＝ax2+bx+c，
∴，
解得，
∴y＝﹣x2+2x+3；
（2）∵DE∥BC，
∴＝，
设直线BC的解析式为y＝kx+b，
∴，
解得，
∴y＝﹣x+3，
设D（t，﹣t2+2t+3），
∴过D点的直线DE的解析式为y＝﹣x﹣t2+3t+3，
∴E（﹣t2+3t+3，0），
∴AE＝﹣t2+3t+4，
∴＝，
当t＝时，有最小值，
∴有最小值，
此时D点横坐标为；
（3）①∵y＝﹣x2+2x+3＝﹣（x﹣1）2+4，
∴G（1，4），H（1，0），
∵GH＝4，BH＝2，
∴tan∠BGH＝，
∵∠MBA＝∠BGH，
∴tan∠MBA＝，
过点M作MK⊥x轴交于K点，
∴＝，
∵M（m，﹣m2+2m+3），
∴MK＝|﹣m2+2m+3|，BK＝|3﹣m|，
∴|3﹣m|＝2|﹣m2+2m+3|，
解得m＝﹣或m＝﹣，
∴M（﹣，）或（﹣，﹣）；
②∵四边形MPNQ恰好为正方形，
∴MN⊥PQ，
∵M、N关于直线x＝1对称，
∴P、Q的横坐标为1，
∵M（m，﹣m2+2m+3），
∴N（2﹣m，﹣m2+2m+3），
∴MN＝|2﹣2m|，
∴|1﹣m|＝|﹣m2+2m+3|，
解得m＝或m＝．
【点评】本题考查二次函数的图象及性质，熟练掌握二次函数的图象及性质，正方形的性质，直角三角形的性质是解题的关键．
a
b
c
d
a
（b，a）
（c，a）
（d，a）
b
（a，b）
（c，b）
（d，b）
c
（a，c）
（b，c）
（d，c）
d
（a，d）
（b，d）
（c，d）