所属成套资源:人教版数学七年级下册期末提升训练专题 (含答案详解)
人教版数学七年级下册期末提升训练专题01 相交线与平行线必刷常考题(含答案详解)
展开
这是一份人教版数学七年级下册期末提升训练专题01 相交线与平行线必刷常考题(含答案详解),共33页。
A.B.
C.D.
2.如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠AB.∠1=∠2
C.∠D=∠DCED.∠D+∠ACD=180°
3.如图,下列条件中,不能判断直线l1∥l2的是( )
A.∠1=∠3 B.∠2=∠3C.∠4=∠5 D.∠2+∠4=180°
4.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
A.30°B.25°C.20°D.15°
5.下列图形中,不能通过其中一个四边形平移得到的是( )
A.B.
C.D.
6.将一直角三角板与两边平行的纸条如图所示放置,下列结论:
(1)∠1=∠2;
(2)∠3=∠4;
(3)∠2+∠4=90°;
(4)∠4+∠5=180°,
其中正确的个数是( )
A.1B.2C.3D.4
7.下列各图中,∠1与∠2是对顶角的是( )
A.B.
C.D.
8.如图,已知∠1=70°,如果CD∥BE,那么∠B的度数为( )
A.70°B.100°C.110°D.120°
9.如图,AB∥CD,∠1=58°,FG平分∠EFD,则∠FGB的度数等于( )
A.122°B.151°C.116°D.97°
10.下列所示的四个图形中,∠1和∠2是同位角的是( )
A.②③B.①②③C.①②④D.①④
11.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.两直线平行,同位角相等
12.某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )
A.甲种方案所用铁丝最长
B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长
D.三种方案所用铁丝一样长
13.如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.如果∠2=60°,那么∠1的度数为( )
A.60°B.50°C.40°D.30°
14.如图,直线l1∥l2,∠A=125°,∠B=85°,则∠1+∠2=( )
A.30°B.35°C.36°D.40°
15.点P是直线l外一点,A、B、C为直线l上的三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线l的距离( )
A.小于2cmB.等于2cmC.不大于2cmD.等于4cm
16.如图,A,B,C,D中的哪幅图案可以通过图案①平移得到( )
A.B.C.D.
17.如图a∥b,M、N分别在a、b上,P为两平行线间一点,那么∠1+∠2+∠3=( )
A.180°B.270°C.360°D.540°
18.如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
A.30°B.20°C.15°D.14°
19.某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( )
A.第一次左拐30°,第二次右拐30°
B.第一次右拐50°,第二次左拐130°
C.第一次右拐50°,第二次右拐130°
D.第一次向左拐50°,第二次向左拐120°
填空题必练
20.把命题“对顶角相等”改写成“如果…那么…”的形式: .
21.如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是 .
22.命题“对顶角相等”的逆命题是 .
23.如图,将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF,则四边形ABFD的周长为 .
24.如图,已知AB∥CD,BE平分∠ABC,∠CDE=150°,则∠C= °.
25.已知三条不同的直线a、b、c在同一平面内,下列四条命题:
①如果a∥b,a⊥c,那么b⊥c;②如果b∥a,c∥a,那么b∥c;③如果b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥c.
其中真命题的是 .(填写所有真命题的序号)
26.一大门的栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= 度.
27.如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2= .
28.如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=25°,则∠2= .
解答题必练
29.如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
∵EF∥AD,( )
∴∠2= .(两直线平行,同位角相等)
又∵∠1=∠2,( )
∴∠1=∠3.( )
∴AB∥DG.( )
∴∠BAC+ =180°( )
又∵∠BAC=70°,( )
∴∠AGD= .
30.已知:如图,AD∥BE,∠1=∠2,求证:∠A=∠E.
31.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
32.如图所示,直线AB、CD相交于O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2和∠3的度数.
33.如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD.
34.如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
35.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
36.已知:如图AB∥CD,EF交AB于G,交CD于F,FH平分∠EFD,交AB于H,∠AGE=50°,求:∠BHF的度数.
37.如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AD∥BC.
38.如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD.
39.如图,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠ACB的大小关系,并说明理由.
40.已知:如图所示,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.
(1)求证:AB∥CD;
(2)试探究∠2与∠3的数量关系.
41.已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.
(1)求证:AB∥CD;
(2)求∠C的度数.
专题01 相交线与平行线必刷常考题
选择题必练
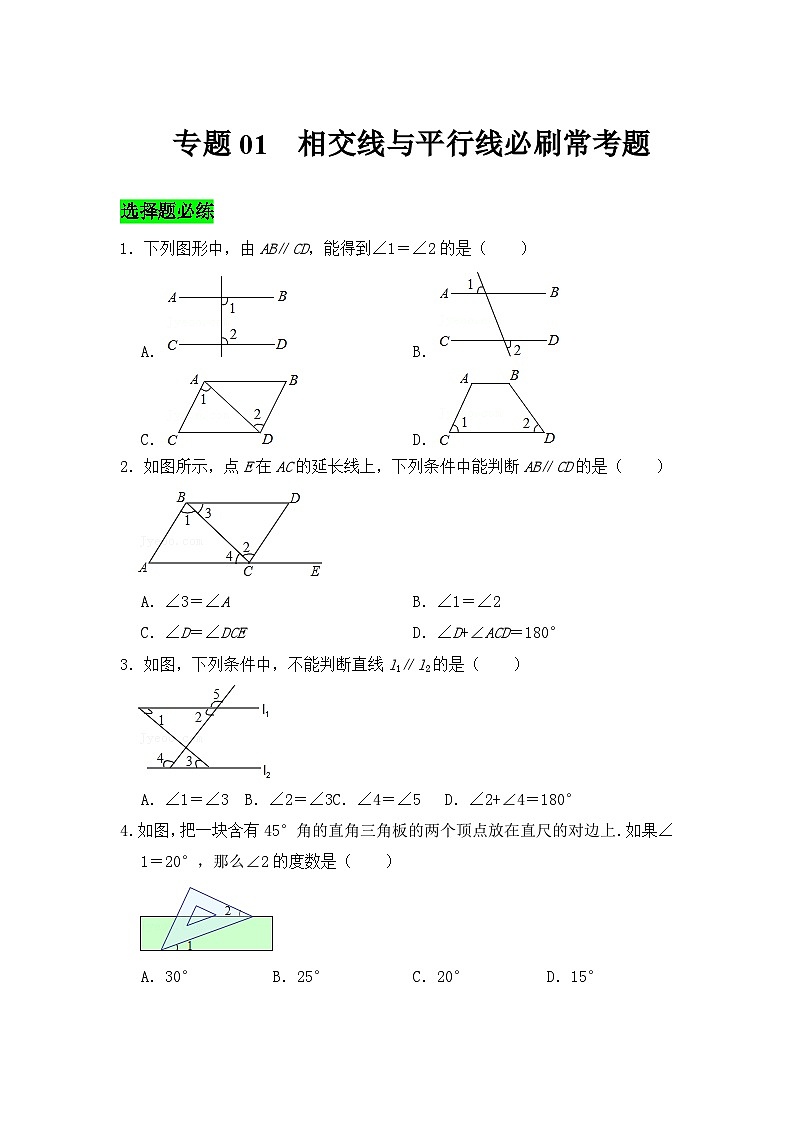
1.下列图形中,由AB∥CD,能得到∠1=∠2的是( )
A.B.
C.D.
【答案】B
【解答】解:A、∵AB∥CD,
∴∠1+∠2=180°,
故A错误;
B、∵AB∥CD,
∴∠1=∠3,
∵∠2=∠3,
∴∠1=∠2,
故B正确;
C、∵AB∥CD,
∴∠BAD=∠CDA,
若AC∥BD,可得∠1=∠2;
故C错误;
D、若梯形ABCD是等腰梯形,可得∠1=∠2,
故D错误.
故选:B.
2.如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠AB.∠1=∠2
C.∠D=∠DCED.∠D+∠ACD=180°
【答案】B
【解答】解:A、∠3=∠A,无法得到,AB∥CD,故此选项错误;
B、∠1=∠2,根据内错角相等,两直线平行可得:AB∥CD,故此选项正确;
C、∠D=∠DCE,根据内错角相等,两直线平行可得:BD∥AC,故此选项错误;
D、∠D+∠ACD=180°,根据同旁内角互补,两直线平行可得:BD∥AC,故此选项错误;
故选:B.
3.如图,下列条件中,不能判断直线l1∥l2的是( )
A.∠1=∠3 B.∠2=∠3C.∠4=∠5 D.∠2+∠4=180°
【答案】B
【解答】解:A、根据内错角相等,两直线平行可判断直线l1∥l2,故此选项不合题意;
B、∠2=∠3,不能判断直线l1∥l2,故此选项符合题意;
C、根据同位角相等,两直线平行可判断直线l1∥l2,故此选项不合题意;
D、根据同旁内角互补,两直线平行可判断直线l1∥l2,故此选项不合题意;
故选:B.
4.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
A.30°B.25°C.20°D.15°
【答案】B
【解答】解:根据题意可知,两直线平行,内错角相等,
∴∠1=∠3,
∵∠3+∠2=45°,
∴∠1+∠2=45°
∵∠1=20°,
∴∠2=25°.
故选:B.
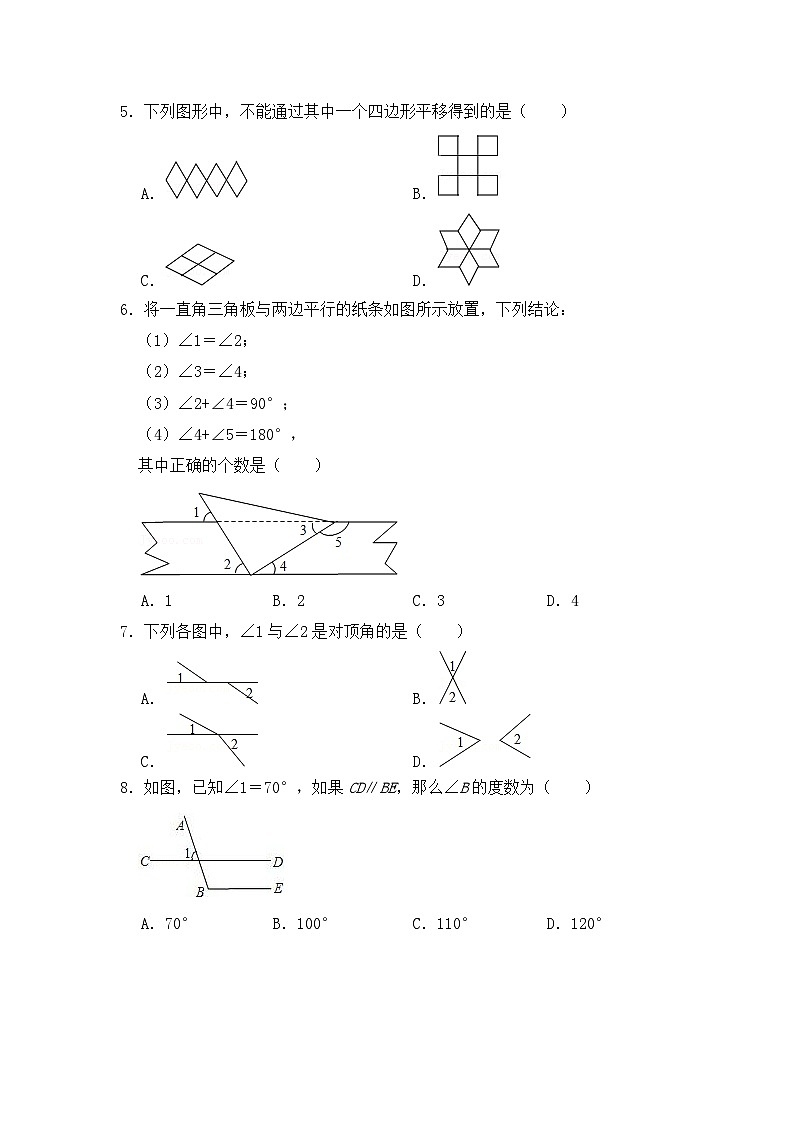
5.下列图形中,不能通过其中一个四边形平移得到的是( )
A.B.
C.D.
【答案】D
【解答】解:A、能通过其中一个四边形平移得到,故本选项不符合题意;
B、能通过其中一个四边形平移得到,故本选项不符合题意;
C、能通过其中一个四边形平移得到,故本选项不符合题意;
D、不能通过其中一个四边形平移得到,需要一个四边形旋转得到,故本选项符合题意.
故选:D.
6.将一直角三角板与两边平行的纸条如图所示放置,下列结论:
(1)∠1=∠2;
(2)∠3=∠4;
(3)∠2+∠4=90°;
(4)∠4+∠5=180°,
其中正确的个数是( )
A.1B.2C.3D.4
【答案】D
【解答】解:∵纸条的两边平行,
∴(1)∠1=∠2(同位角);
(2)∠3=∠4(内错角);
(4)∠4+∠5=180°(同旁内角)均正确;
又∵直角三角板与纸条下线相交的角为90°,
∴(3)∠2+∠4=90°,正确.
故选:D.
7.下列各图中,∠1与∠2是对顶角的是( )
A.B.
C.D.
【答案】B
【解答】解:A、∠1与∠2不是对顶角,故A选项错误;
B、∠1与∠2是对顶角,故B选项正确;
C、∠1与∠2不是对顶角,故C选项错误;
D、∠1与∠2不是对顶角,故D选项错误.
故选:B.
8.如图,已知∠1=70°,如果CD∥BE,那么∠B的度数为( )
A.70°B.100°C.110°D.120°
【答案】C
【解答】解:如图,∵∠1=70°,
∴∠2=∠1=70°,
∵CD∥BE,
∴∠B=180°﹣∠1=180°﹣70°=110°.
故选:C.
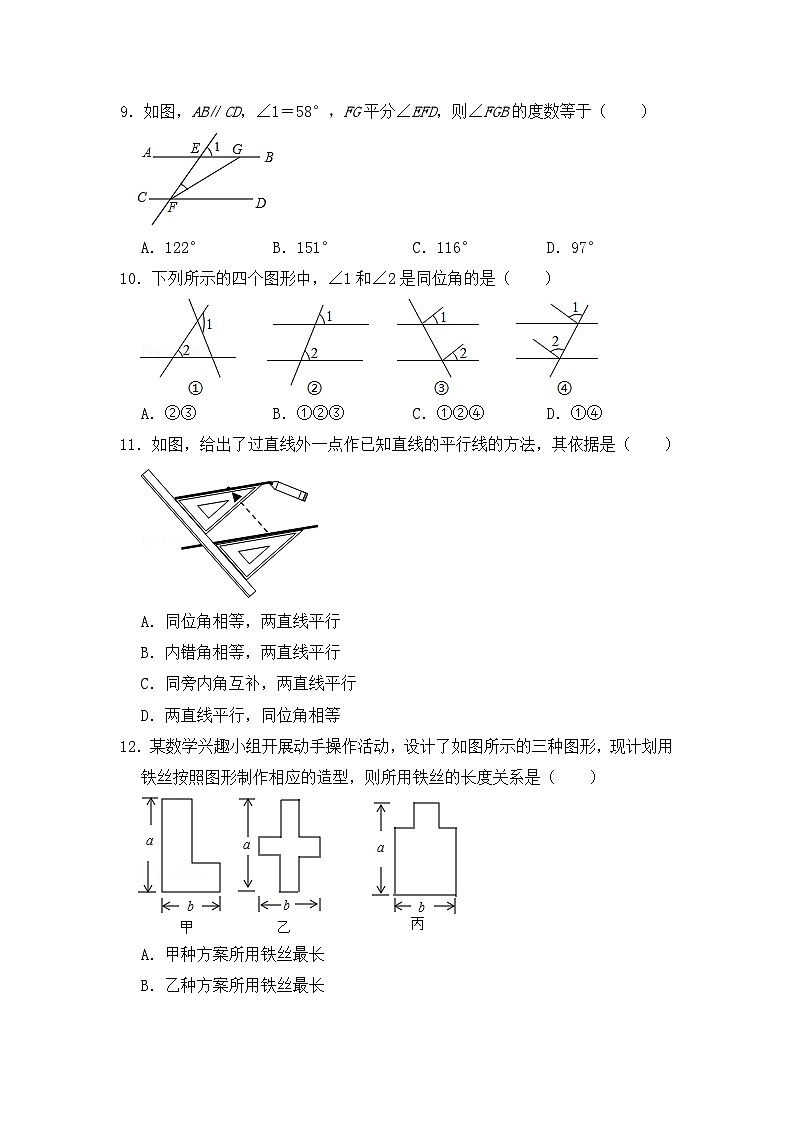
9.如图,AB∥CD,∠1=58°,FG平分∠EFD,则∠FGB的度数等于( )
A.122°B.151°C.116°D.97°
【答案】B
【解答】解:∵AB∥CD,∠1=58°,
∴∠EFD=∠1=58°,
∵FG平分∠EFD,
∴∠GFD=∠EFD=×58°=29°,
∵AB∥CD,
∴∠FGB=180°﹣∠GFD=151°.
故选:B.
10.下列所示的四个图形中,∠1和∠2是同位角的是( )
A.②③B.①②③C.①②④D.①④
【答案】C
【解答】解:图①、②、④中,∠1与∠2在截线的同侧,并且在被截线的同一方,是同位角;
图③中,∠1与∠2的两条边都不在同一条直线上,不是同位角.
故选:C.
11.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.两直线平行,同位角相等
【答案】A
【解答】解:图中所示过直线外一点作已知直线的平行线,则利用了同位角相等,两直线平行的判定方法.
故选:A.
12.某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )
A.甲种方案所用铁丝最长
B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长
D.三种方案所用铁丝一样长
【答案】D
【解答】解:由图形可得出:甲所用铁丝的长度为:2a+2b,
乙所用铁丝的长度为:2a+2b,
丙所用铁丝的长度为:2a+2b,
故三种方案所用铁丝一样长.
故选:D.
13.如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.如果∠2=60°,那么∠1的度数为( )
A.60°B.50°C.40°D.30°
【答案】D
【解答】解:如图,
∵∠3=∠1+30°,
∵AB∥CD,
∴∠2=∠3=60°,
∴∠1=∠3﹣30°=60°﹣30°=30°.
故选:D.
14.如图,直线l1∥l2,∠A=125°,∠B=85°,则∠1+∠2=( )
A.30°B.35°C.36°D.40°
【答案】A
【解答】解:如图,过点A作l1的平行线,过点B作l2的平行线,
∴∠3=∠1,∠4=∠2,
∵l1∥l2,
∴AC∥BD,
∴∠CAB+∠ABD=180°,
∴∠3+∠4=125°+85°﹣180°=30°,
∴∠1+∠2=30°.
故选:A.
15.点P是直线l外一点,A、B、C为直线l上的三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线l的距离( )
A.小于2cmB.等于2cmC.不大于2cmD.等于4cm
【答案】C
【解答】解:∵直线外一点与直线上各点连接的所有线段中,垂线段最短,
∴点P到直线l的距离≤PA,
即点P到直线l的距离不大于2.
故选:C.
16.如图,A,B,C,D中的哪幅图案可以通过图案①平移得到( )
A.B.C.D.
【答案】D
【解答】解:通过图案①平移得到必须与图案①完全相同,角度也必须相同,
观察图形可知D可以通过图案①平移得到.
故选:D.
17.如图a∥b,M、N分别在a、b上,P为两平行线间一点,那么∠1+∠2+∠3=( )
A.180°B.270°C.360°D.540°
【答案】C
【解答】解:过点P作PA∥a,则a∥b∥PA,
∴∠1+∠MPA=180°,∠3+∠NPA=180°,
∴∠1+∠2+∠3=360°.
故选:C.
18.如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
A.30°B.20°C.15°D.14°
【答案】C
【解答】解:如图,∠2=30°,
∠1=∠3﹣∠2=45°﹣30°=15°.
故选:C.
19.某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( )
A.第一次左拐30°,第二次右拐30°
B.第一次右拐50°,第二次左拐130°
C.第一次右拐50°,第二次右拐130°
D.第一次向左拐50°,第二次向左拐120°
【答案】A
【解答】解:如图所示(实线为行驶路线):
A符合“同位角相等,两直线平行”的判定,其余均不符合平行线的判定.
故选:A.
填空题必练
20.把命题“对顶角相等”改写成“如果…那么…”的形式: .
【答案】如果两个角是对顶角,那么这两个角相等.
【解答】解:题设为:两个角是对顶角,结论为:这两个角相等,
故写成“如果…那么…”的形式是:如果两个角是对顶角,那么这两个角相等,
故答案为:如果两个角是对顶角,那么这两个角相等.
21.如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是 .
【答案】垂线段最短.
【解答】解:根据垂线段定理,连接直线外一点与直线上各点的所有线段中,垂线段最短,
∴沿AB开渠,能使所开的渠道最短.
故答案为:垂线段最短.
22.命题“对顶角相等”的逆命题是 .
【答案】相等的角为对顶角.
【解答】解:命题“对顶角相等”的逆命题是“相等的角为对顶角”.
故答案为:相等的角为对顶角.
23.如图,将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF,则四边形ABFD的周长为 .
【答案】10.
【解答】解:根据题意,将周长为8的△ABC沿边BC向右平移1个单位得到△DEF,
则AD=1,BF=BC+CF=BC+1,DF=AC,
又∵AB+BC+AC=8,
∴四边形ABFD的周长=AD+AB+BF+DF=1+AB+BC+1+AC=10.
故答案为:10.
24.如图,已知AB∥CD,BE平分∠ABC,∠CDE=150°,则∠C= °.
【答案】120.
【解答】解:∵∠CDE=150°,
∴∠CDB=180﹣∠CDE=30°,
又∵AB∥CD,
∴∠ABD=∠CDB=30°;
∵BE平分∠ABC,
∴∠ABC=60°,
∴∠C=180°﹣60°=120°.
故答案为:120.
25.已知三条不同的直线a、b、c在同一平面内,下列四条命题:
①如果a∥b,a⊥c,那么b⊥c;②如果b∥a,c∥a,那么b∥c;③如果b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥c.
其中真命题的是 .(填写所有真命题的序号)
【答案】①②④
【解答】解:①如果a∥b,a⊥c,那么b⊥c是真命题,故①正确;
②如果b∥a,c∥a,那么b∥c是真命题,故②正确;
③如果b⊥a,c⊥a,那么b⊥c是假命题,故③错误;
④如果b⊥a,c⊥a,那么b∥c是真命题,故④正确.
故答案为:①②④.
26.一大门的栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= 度.
【答案】270
【解答】解:过B作BF∥AE,则CD∥BF∥AE.
∴∠BCD+∠1=180°;
又∵AB⊥AE,
∴AB⊥BF.
∴∠ABF=90°.
∴∠ABC+∠BCD=90°+180°=270°.
故答案为:270.
27.如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2= .
【答案】140°
【解答】解:如图,
∵l1∥l2,
∴∠3=∠1=40°,
∵∠α=∠β,
∴AB∥CD,
∴∠2+∠3=180°,
∴∠2=180°﹣∠3=180°﹣40°=140°.
故答案为140°.
28.如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=25°,则∠2= .
【答案】115°
【解答】解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠2=∠DEG=∠1+∠FEG=115°.
故答案为:115°.
解答题必练
29.如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
∵EF∥AD,( )
∴∠2= .(两直线平行,同位角相等)
又∵∠1=∠2,( )
∴∠1=∠3.( )
∴AB∥DG.( )
∴∠BAC+ =180°( )
又∵∠BAC=70°,( )
∴∠AGD= .
【答案】略
【解答】解:∵EF∥AD(已知),
∴∠2=∠3.(两直线平行,同位角相等)
又∵∠1=∠2,(已知)
∴∠1=∠3,(等量代换)
∴AB∥DG.(内错角相等,两直线平行)
∴∠BAC+∠AGD=180°.(两直线平行,同旁内角互补)
又∵∠BAC=70°,(已知)
∴∠AGD=110°.
30.已知:如图,AD∥BE,∠1=∠2,求证:∠A=∠E.
【答案】略
【解答】证明:∵AD∥BE,
∴∠A=∠3,
∵∠1=∠2,
∴DE∥AC,
∴∠E=∠3,
∴∠A=∠EBC=∠E.
31.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
【答案】20°
【解答】解:∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠ACB+∠DAC=180°,
∵∠DAC=120°,
∴∠ACB=60°,
又∵∠ACF=20°,
∴∠FCB=∠ACB﹣∠ACF=40°,
∵CE平分∠BCF,
∴∠BCE=20°,
∵EF∥BC,
∴∠FEC=∠ECB,
∴∠FEC=20°.
32.如图所示,直线AB、CD相交于O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2和∠3的度数.
【答案】∠2=65°,∠3=50°
【解答】解:∵∠FOC=90°,∠1=40°,AB为直线,
∴∠3+∠FOC+∠1=180°,
∴∠3=180°﹣90°﹣40°=50°.
∠3与∠AOD互补,
∴∠AOD=180°﹣∠3=130°,
∵OE平分∠AOD,
∴∠2=∠AOD=65°.
33.如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD.
【答案】110°
【解答】解:∵EF∥AD(已知)
∴∠2=∠3(两直线平行,同位角相等);
∵∠1=∠2(已知),
∴∠1=∠3(等量代换);
∴DG∥AB(内错角相等,两直线平行).
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补).
∵∠BAC=70°,
∴∠AGD=110°.
34.如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
【答案】50°
【解答】解:∵AB∥CD,
∴∠ABC=∠1=65°,∠ABD+∠BDC=180°,
∵BC平分∠ABD,
∴∠ABD=2∠ABC=130°,
∴∠BDC=180°﹣∠ABD=50°,
∴∠2=∠BDC=50°.
35.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
【答案】20°
【解答】解:∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠ACB+∠DAC=180°,
∵∠DAC=120°,
∴∠ACB=60°,
又∵∠ACF=20°,
∴∠FCB=∠ACB﹣∠ACF=40°,
∵CE平分∠BCF,
∴∠BCE=20°,
∵EF∥BC,
∴∠FEC=∠ECB,
∴∠FEC=20°.
36.已知:如图AB∥CD,EF交AB于G,交CD于F,FH平分∠EFD,交AB于H,∠AGE=50°,求:∠BHF的度数.
【答案】115°
【解答】解:∵AB∥CD,
∴∠CFG=∠AGE=50°,
∴∠GFD=130°;
又∵FH平分∠EFD,
∴∠HFD=∠EFD=65°,
∵AB∥CD,
∴∠BHF+∠HFD=180°,
∴∠BHF=180°﹣∠HFD=115°.
37.如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AD∥BC.
【答案】略
【解答】证明:∵AE平分∠BAD,
∴∠1=∠2,
∵AB∥CD,∠CFE=∠E,
∴∠1=∠CFE=∠E,
∴∠2=∠E,
∴AD∥BC.
38.如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD.
【答案】110°
【解答】解:∵EF∥AD(已知)
∴∠2=∠3(两直线平行,同位角相等);
∵∠1=∠2(已知),
∴∠1=∠3(等量代换);
∴DG∥AB(内错角相等,两直线平行).
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补).
∵∠BAC=70°,
∴∠AGD=110°.
39.如图,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠ACB的大小关系,并说明理由.
【答案】略
【解答】解:∠AED=∠ACB.
理由:∵∠1+∠4=180°(平角定义),∠1+∠2=180°(已知).
∴∠2=∠4.
∴EF∥AB(内错角相等,两直线平行).
∴∠3=∠ADE(两直线平行,内错角相等).
∵∠3=∠B(已知),
∴∠B=∠ADE(等量代换).
∴DE∥BC(同位角相等,两直线平行).
∴∠AED=∠ACB(两直线平行,同位角相等).
40.已知:如图所示,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.
(1)求证:AB∥CD;
(2)试探究∠2与∠3的数量关系.
【答案】(1)略(2)90°
【解答】证明:(1)∵BE、DE平分∠ABD、∠BDC,
∴∠1=∠ABD,∠2=∠BDC;
∵∠1+∠2=90°,
∴∠ABD+∠BDC=180°;
∴AB∥CD;(同旁内角互补,两直线平行)
解:(2)∵DE平分∠BDC,
∴∠2=∠FDE;
∵∠1+∠2=90°,
∴∠BED=180﹣(∠1+∠2)=90°=∠DEF=90°;
∴∠3+∠FDE=90°;
∴∠2+∠3=90°.
41.已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.
(1)求证:AB∥CD;
(2)求∠C的度数.
【答案】(1)略 (2)25°
【解答】(1)证明:∵AE⊥BC,FG⊥BC,
∴AE∥GF,
∴∠2=∠A,
∵∠1=∠2,
∴∠1=∠A,
∴AB∥CD;
(2)解:∵AB∥CD,
∴∠D+∠CBD+∠3=180°,
∵∠D=∠3+60°,∠CBD=70°,
∴∠3=25°,
∵AB∥CD,
∴∠C=∠3=25°.
相关试卷
这是一份人教版数学七下期末提升训练专题05 一元一次不等式组必刷常考题(含答案详解),共15页。试卷主要包含了若x>y,则下列式子中错误的是,下列说法不一定成立的是,不等式组的解集在数轴上表示为,如果关于x的不等式,如果点P,不等式组的最小整数解为等内容,欢迎下载使用。
这是一份人教版数学七下期末提升训练专题04 二元一次方程组必刷常考题(含答案详解),共30页。试卷主要包含了方程组的解是,已知,满足方程组,则的值为等内容,欢迎下载使用。
这是一份2024-2025学年-人教版数学七年级上册期末必刷常考题:代数式,共14页。









