
所属成套资源:(安徽版)中考数学一轮复习专题训练 (含答案)
(安徽版)中考数学一轮复习专题训练专题15 图形认识初步(含答案)
展开
这是一份(安徽版)中考数学一轮复习专题训练专题15 图形认识初步(含答案),共24页。试卷主要包含了单选题,填空题等内容,欢迎下载使用。
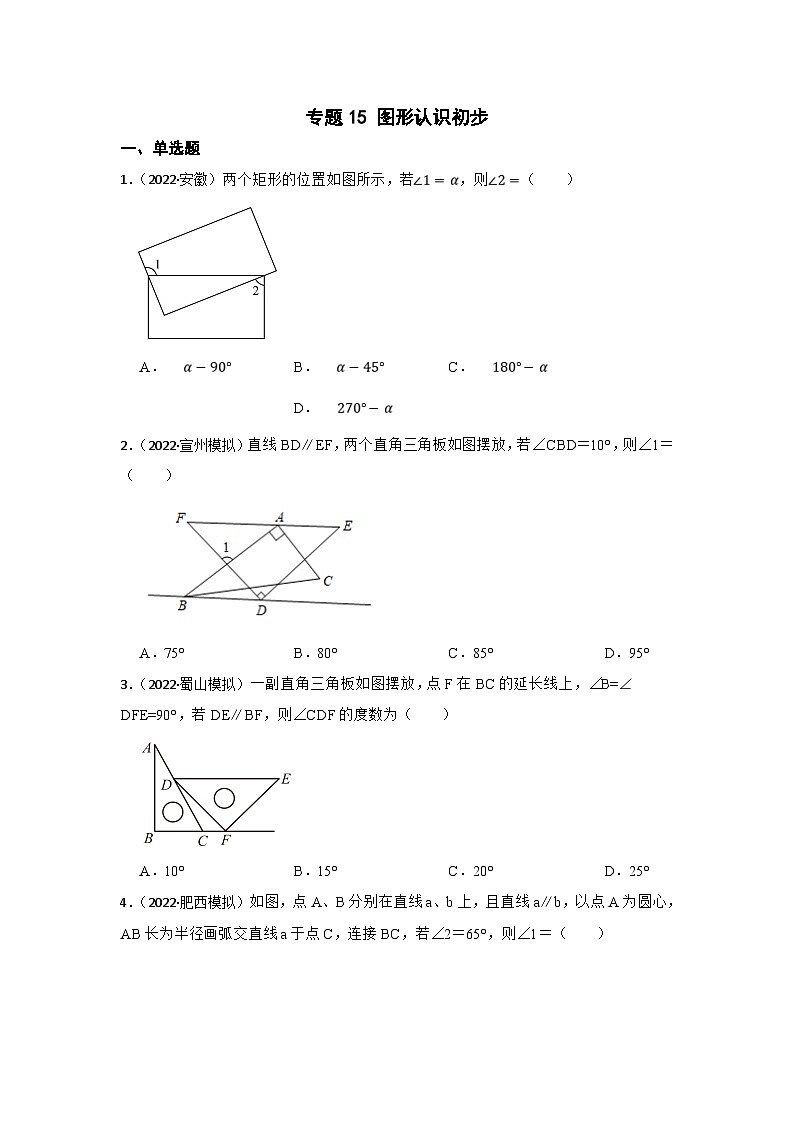
1.(2022·安徽)两个矩形的位置如图所示,若,则( )
A.B.C.D.
2.(2022·宣州模拟)直线BD∥EF,两个直角三角板如图摆放,若∠CBD=10°,则∠1=( )
A.75°B.80°C.85°D.95°
3.(2022·蜀山模拟)一副直角三角板如图摆放,点F在BC的延长线上,∠B=∠DFE=90°,若DE∥BF,则∠CDF的度数为( )
A.10°B.15°C.20°D.25°
4.(2022·肥西模拟)如图,点A、B分别在直线a、b上,且直线a∥b,以点A为圆心,AB长为半径画弧交直线a于点C,连接BC,若∠2=65°,则∠1=( )
A.75°B.65°C.50°D.25°
5.(2022·蜀山模拟)两个直角三角板ABC,ADE如图摆放,其中∠BAC=∠DEA = 90°,∠B=45°,∠D=60°,若DEBC,则∠BAD的大小为( )
A.15°B.22.5°C.30°D.45°
6.(2022·宣城模拟)将两个直角三角板如图摆放,其中 , , , 与 交于点P, 与 交于点Q.若 ,则 ()
A.40°B.32.5°C.45.5°D.30°
7.(2022·肥西模拟)如图,直线,直线分别交直线、于点E、F,过点F作,交直线于点G,若,则的大小是( )
A.B.C.D.
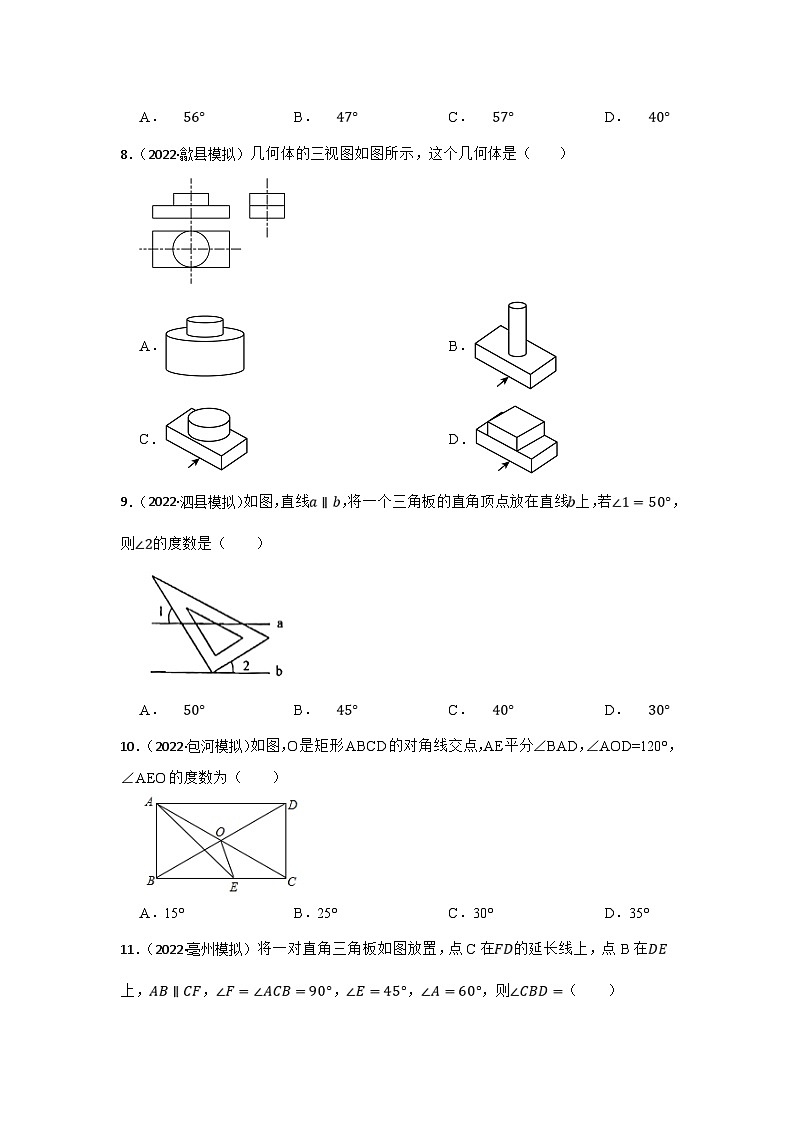
8.(2022·歙县模拟)几何体的三视图如图所示,这个几何体是( )
A.B.
C.D.
9.(2022·泗县模拟)如图,直线,将一个三角板的直角顶点放在直线上,若,则的度数是( )
A.B.C.D.
10.(2022·包河模拟)如图,O是矩形ABCD的对角线交点,AE平分∠BAD,∠AOD=120°,∠AEO的度数为( )
A.15°B.25°C.30°D.35°
11.(2022·亳州模拟)将一对直角三角板如图放置,点C在的延长线上,点B在上,,,,,则( )
A.B.C.D.
12.(2022·安徽模拟)如图,上有A、B两点,点C为弧AB上一点,点P是外一点,且,,则的度数为( )
A.B.C.D.
13.(2021·安徽模拟)如图, , .若 ,则 的度数是( )
A.40°B.60°C.70°D.90°
14.(2021·安徽)在△ABC中∠ACB=90°,分别过点B,C作∠BAC平分线的垂线,垂足分别为点D,E,BC的中点是M,连接CD,MD,ME.则下列结论错误的是( )
A.CD=2MEB.ME∥ABC.BD=CDD.ME=MD
15.(2021·合肥模拟)如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含 角的直角三角板的斜边与纸条一边重合,含 角的三角板的一个顶点在纸条的另一边上,则 的度数是( )
A.B.C.D.
16.(2021·包河模拟)如图,AB//CD,∠1+∠2=110°,则∠GEF+∠GFE的度数为( )
A.110°B.70°C.80°D.90°
17.(2021·芜湖模拟)在数学课上,小明同学在练习本上相互平行的横格线上先画了直线 ,度量出 ,接着他准备在点 处画直线 ,若要使 ,则 的度数为( )
A.65°B.75°C.85°D.105°
18.(2021·安徽模拟)如图,一副直角三角板的顶点 重合( , ),当 时,则∠ABD=( )
A.105°B.75°C.85°D.95°
19.(2021·包河模拟)一副三角板如图放置,则 的度数为( )
A.B.C.D.
20.(2021·义安模拟)如图,在 中, , , ,则 大小为( )
A.B.C.D.
二、填空题
21.(2022·义安模拟)在中,D,E是直线上两点,且,,若,则= .
22.(2022·肥西模拟)如图,在△ABC中,AB=4,点P为AC边上一点,PE⊥AB于点E,PF⊥BC于点F,将∠A、∠C分别沿PE、PF折叠,使点A、C分别落在边AB、BC上的点G、H处.
(1)当∠B=50°时,则∠GPH= .
(2)当四边形BHPG为平行四边形时,则PE+PF的值为 .
23.(2021·义安模拟)如图, , 分别是 的边 , 上的点,若 , , ,则 的大小为 .
24.(2021·庐阳模拟)在正方形网格中,A,B,C,D,E均为格点,则∠BAC-∠DAE= °.
25.(2021·安徽模拟)如图, , ,∠BEC=40°,则 °.
答案解析部分
1.【答案】C
【解析】【解答】解:如图,
∠3=∠1-90°=α-90°,
∠2=90°-∠3=180°-α.
故答案为:C.
【分析】先利用三角形的外角的性质求出∠3=∠1-90°=α-90°,再利用余角的性质可得∠2=90°-∠3=180°-α。
2.【答案】D
【解析】【解答】解:∵△ABC是含30°的三角板,△DEF为含45°的三角板,
∴∠ABC=30°,∠F=45°,
∵∠CBD=10°,
∴∠ABD=∠ABC+∠CBD=30°+10°=40°,
∵EF∥BD,
∴∠FAB=∠ABD=40°,
∴∠1=180°-∠F-∠FAB=180°-45°-40°=95°.
故答案为:D.
【分析】先由已知条件得出∠ABD,再根据平行线的性质得出∠FAB,再根据三角形内角和定理即可求解。
3.【答案】B
【解析】【解答】如图,
∵DE∥BF,∠B=∠DFE=90°,
∴∠EDF=∠2=45°,∠ACB=60°,
∵∠ACB=∠2+∠CDF,
∴∠CDF=15°,
故答案为:B.
【分析】利用平行线的性质可得∠EDF=∠2=45°,∠ACB=60°,再利用角的运算可得∠CDF=15°。
4.【答案】C
【解析】【解答】解:,,
,
由作图过程可知,,
,
,
故答案为:C.
【分析】根据平行线的性质可得,再利用等边对顶角的性质可得,最后利用角的运算可得。
5.【答案】A
【解析】【解答】解:∵DE∥BC,∠BAC=∠DEA = 90°,
∴AE⊥BC,
∵∠B=45°,∠D=60°,
∴∠BAE=45°,∠DAE=30°.
∴∠BAD=45°-30°=15°.
故答案为:A
【分析】先求出∠BAE=45°,∠DAE=30°,再利用∠BAD=∠BAE-∠DAE计算即可。
6.【答案】D
【解析】【解答】解:在 中, , ,则 ,
在 中, , ,则 ,
,
, ,
, ,
,
故答案为:D.
【分析】根据平行线的性质可得 , ,再利用三角形的外角的性质可得∠DPC和∠DQC,最后利用角的运算可得。
7.【答案】B
【解析】【解答】解:∵,
∴∠EFD=∠1=43°,
∵,
∴∠GFE=90°,
∴∠2=180°-90°-43°=47°.
故答案为:B.
【分析】根据平行同位角相等、对顶角相等和余角的性质,可知∠2=90°-∠1
8.【答案】C
【解析】【解答】解:由几何体的三视图,可得这个几何体是
故答案为:C.
【分析】根据几何体的三视图得到答案
9.【答案】C
【解析】【解答】如图,
一个三角板的直角顶点放在直线上
故答案为:C.
【分析】根据平行线的性质可得,再利用角的运算可得。
10.【答案】C
【解析】【解答】解:∵四边形ABCD是矩形,
∴AD//BC,∠ABC=∠BAD=90°,AC=BD,OB=BD,OC=AC,
∴OB=OC,
∴∠OBC=∠OCB,
∵∠BOC=∠AOD=120°,
∴∠OBC=30°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=45°,
∴∠AEB=∠EAD=∠BAE=45°,
∴AB=BE,
∵∠AOD=120°,
∴∠AOB=60°,
∴AB=OA=OB,
∴OB=BE,
∴∠BOE=∠BEO,
∴∠OEB=75°,
∴∠AEO=∠OEB-∠AEB=75°-45°=30°,
故答案为:C.
【分析】根据矩形的性质得出OB=OC,∠ABC=∠BAD=90°,AC=BD,OB=BD,OC=AC,由AE平分∠BAD,得出∠BAE、∠AEB的度数,及是等边三角形,是等腰三角形,即可得出是等腰三角形,可求出∠OEB的度数,即可得解。
11.【答案】B
【解析】【解答】解:∵,,,
∴∠EDF=,∠ABC=,
∵AB∥CF,
∴∠ABD=∠EDF=,
∴∠CBD=∠ABD-∠ABC=,
故答案为:B.
【分析】先利用平行线的性质可得∠ABD=∠EDF=45°,再利用∠CBD=∠ABD-∠ABC计算即可。
12.【答案】D
【解析】【解答】解:如图,在优弧AB上找一点D,连接AD,BD,AB,则∠ADB=∠AOB=30°
在圆内接四边形ADBC中
∠ACB=180°-∠ADB=180°-30°=150°
∴∠CAB+∠CBA=180°-150°=30°
又∵AC=BC=PC
∴∠CPA=∠CAP,∠CBP=∠CPB
∴∠APB=180°-(∠PAB+∠PBA)
=180°-(∠CAB+∠CBA+∠CAP+∠CBP)
=180°-30°-(∠CAP+∠CBP)
=150°-(∠CAP+∠CBP)
=150°-(∠APC+∠BPC)
=150°-∠APB
∴∠APB=75°
故答案为:D.
【分析】连接AD,BD,AB,先利用圆周角求出∠ADB=∠AOB=30°,再利用圆内接四边形的性质可得∠ACB=180°-∠ADB=180°-30°=150°,再根据等腰三角形和三角形的内角和求出∠CAB+∠CBA=180°-150°=30°,最后利用∠APB=180°-(∠PAB+∠PBA)=150°-(∠APC+∠BPC)=150°-∠APB计算即可。
13.【答案】D
【解析】【解答】解:如图所示,过点C作BD的平行线CF交AB于点F.
∴ .
∴ .
又∵ ,
∴ .
∵ ,
∴ .
∴ .
又∵ ,
∴ .
∴ .
故答案为:D.
【分析】过点C作BD的平行线CF交AB于点F.根据平行线的性质可得:,,再相加即可。
14.【答案】A
【解析】【解答】解:
根据题意可得,如图所示,延长EM交BD于点F,延长DM交AB于点N
在△ABC中,∠ACB=90°,分别过点B和点C做∠BAC的平分线的垂线,垂足分别为点D和点E
由此可得,点A,C,D,B四点共圆
∵AD评分∠CAB
∴∠CAD=∠BAD
∴CD=DB,即选项C正确;
∵点M为BC的中点
∴DM⊥BC
∵∠ACB=90°
∴AC∥DN
∴点N为线段AB的中点
∴AN=DN
∴∠DAB=∠ADN
∵CE⊥AD,BD⊥AD
∴CE∥BD
∴∠ECM=∠FBM,∠CEM=∠BFM
∵点M为BC的中点
∴CM=BM
∴△CEM≌△BFM
∴EM=FM
∴EM=FM=DM,即D正确
∴∠FEM=∠MDE=∠DAB
∴EM∥AB,即选项B正确
∴A不正确
故答案为:A.
【分析】根据题意做出图形,由中点的性质,结合三角形全等的判定和性质,分别判断即可。
15.【答案】B
【解析】【解答】解:过含 角的三角板的直角顶点做一条平行纸条边的线,在图上分别标出 、 、 、 ,
由题意及根据两直线平行知: , ,
所求 ,
由图可知: 与 互补,
,
,
,
故答案为:B.
【分析】先求出 ,再求出∠3=∠4=60°,最后求解即可。
16.【答案】B
【解析】【解答】∵ ,
∴ ,
∴ ,
∵ ,
∴ .
故答案为:B.
【分析】先求出∠BEF+∠DFE=180°,再根据 ∠1+∠2=110°计算求解即可。
17.【答案】B
【解析】【解答】解:如图,由题意得: ,
,
要使 ,则 ,
,
,
,
故答案为:B.
【分析】先求出 ,再求出∠3=75°,最后求解即可。
18.【答案】A
【解析】【解答】解:过点B作MN∥AC,
在Rt△ABC中,∠C=30°,
∴∠A=60°,
∵MN∥AC,
∴∠ABM=∠A=60°,
同理,∠DBM=∠D=45°,
∴∠ABD=∠ABM+∠DBM=105°.
故答案为:A.
【分析】过点B作MN∥AC,根据平行线的性质及∠ABD=∠ABM+∠DBM即可求解.
19.【答案】B
【解析】【解答】如图,∵ ,
∴①,
∵ ,
∴ ,
∵ ,
∴ .
∴ ,
∵ ,
∴②
由①-②得: ,
∴ .
故答案为:B.
【分析】根据∠DAC是△ABD的外角,∠EAC是△ABE的外角得出∠DAC=∠1+∠ABD,∠EAC=∠2+∠ABE,将两式相加即可。
20.【答案】D
【解析】【解答】∵AD∥BC
∴∠B+∠BAD=180°
∵∠B=40°
∴∠BAD=120°
∵∠BAC=40°
∴∠DAC=∠BAD-∠BAC=120°-40°=80°
故答案为:D
【分析】根据AD∥BC,得∠B+∠BAD=180°,则有∠BAD=120°, 再由∠BAC=40°,即得所求结果.
21.【答案】30°或60°或120°
【解析】【解答】解:当点D、E在线段BC上时,
如图1(i),
∵AD=BD,
∴∠B=∠BAD,
∴∠ADE=∠B+∠BAD=2∠BAD,
∵AE=CE,
∴∠C=∠CAE,
∴∠AED=∠C+∠CAE=2∠CAE,
∴∠ADE+∠AED=2(∠BAD+∠CAE),
∵∠ADE+∠AED+∠DAE=180°,∠DAE=60°,
∴∠BAD+∠CAE=60°,
∴∠BAC=∠BAD+∠CAE+∠DAE=120°;
如图1(ii),同理可得∠BAC=120°;
当点D与点C重合,点E与点B重合时,如图2,
∴∠BAC=∠DAE=60°;
当D、E在CB或BC延长线上时,
如图3(i),
∵AD=BD,
∴∠ABD=∠BAD,
∵AE=CE,
∴∠C=∠CAE,
∵∠ABD=∠C+∠BAC,
∴∠BAD=∠C+∠BAC,
∴∠DAE+∠EAB=∠C+∠BAC,
∴∠DAE+∠EAC-∠BAC =∠C+∠BAC,
∴60°=2∠BAC,
∴∠BAC=30°,
如图3(ii),同理可得∠BAC=30°,
综上,∠BAC=30°或60°或120°.
故答案为:30°或60°或120°.
【分析】由等腰三角形的性质可得∠B=∠BAD,∠C=∠CAE,利用三角形的内角和定理可求出∠BAD+∠CAE=60°,进而可求解∠BAC的度数。
22.【答案】(1)80°
(2)2
【解析】【解答】(1)当∠B=50°时,则∠A+∠C=130°,
由折叠可得,∠AGP=∠A,∠PHC=∠C,
∴∠AGP+∠PHC=130°,
∴∠APG+∠CPH=(180°-∠A-∠AGP)+(180°-∠C-∠PHC)=360°-(∠A+∠C)-(∠AGP+∠PHC)=100°,
∴∠GPH=180°-(∠APG+∠CPH)=80°,
故答案为:80°;
(2)当四边形BHPG为平行四边形时,ABPH,GPBC,
∴∠AGP=∠B,∠PHC=∠B,
∵∠AGP=∠A,∠PHC=∠C,
∴∠A=∠B=∠C,
∴△ABC是等边三角形,AC=AB=4,
∴在Rt△AGP和Rt△PCF中,PE+PF=APcs60°+PCcs60°=(AP+PC)cs60°=ACcs60°=4×=,
故答案为:.
【分析】(1)根据三角形的内角和与折叠的性质即可求解;
(2)根据四边形BHPG为平行四边形时得出△ABC是等边三角形,AC=AB=4,再根据解直角三角形的性质即可求解。
23.【答案】40°
【解析】【解答】解:∵AB=AC,
∴∠B=∠ACB,
∵AD=AE,
∴∠ADE=∠AED,
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=∠ADE+20°,
∵∠AED是△EDC的外角,
∴∠AED=∠ACB+20°,
∴∠BAD=∠ADE+20°-∠B=∠ACB+20°+20°-∠B=40°.
故答案为40°.
【分析】先求出∠ADE=∠AED,再求出∠AED=∠ACB+20°,最后计算求解即可。
24.【答案】45
【解析】【解答】解:如图示,在正方形网格中,连接正方形的顶点,得到 和 ,
设正方形网格的边长为1,则有 , , ,
∴ , ,
∴
,
,
,
,
又∵根据作图可知 ,
∴
∴
即有: ,
故答案为:45.
【分析】在正方形网格中,连接正方形的顶点,作出 和 ,设正方形网格的边长为1,则有 , , ,可知 ,可证 ,可得 ,则可证出 ,根据作图可知 ,得 ,可以求出 .
25.【答案】35
【解析】【解答】解:∵EB=EC,∠BEC=40°,
∴∠B=∠ECB= = =70°,
∵∠AEB=70°,∠BEC=40°,
∴∠AEC=∠AEB+∠BEC=70°+40°=110°,
∵EA=EC,
∴∠ECA=∠A= = =35°,
∴∠ACB=∠ECB-∠ECA=70°-35°=35°,
故答案为:35.
【分析】利用等腰三角形的性质和已知角求得∠ECB的度数,然后求得∠ECA的度数后即可求得答案
相关试卷
这是一份专题十二 图形的初步认识——2024届中考数学一轮复习进阶训练,共13页。试卷主要包含了下列说法中正确的选项是,5°B,如图,,,则,,之间的关系是,已知命题等内容,欢迎下载使用。
这是一份专题训练16:图形初步认识 中考数学一轮复习知识点课标要求,共16页。试卷主要包含了知识要点,课标要求,常见考点,专题训练等内容,欢迎下载使用。
这是一份专题15 图形的认识 中考数学一轮复习专题训练(北京专用),共24页。试卷主要包含了单选题,填空题,作图题,综合题等内容,欢迎下载使用。










