浙教版数学七年级上学期期中【压轴23题专练】（解析版）

这是一份浙教版数学七年级上学期期中【压轴23题专练】（解析版），文件包含浙教版数学七年级上学期期中压轴23题专练原卷版doc、浙教版数学七年级上学期期中压轴23题专练解析版doc等2份试卷配套教学资源，其中试卷共33页， 欢迎下载使用。
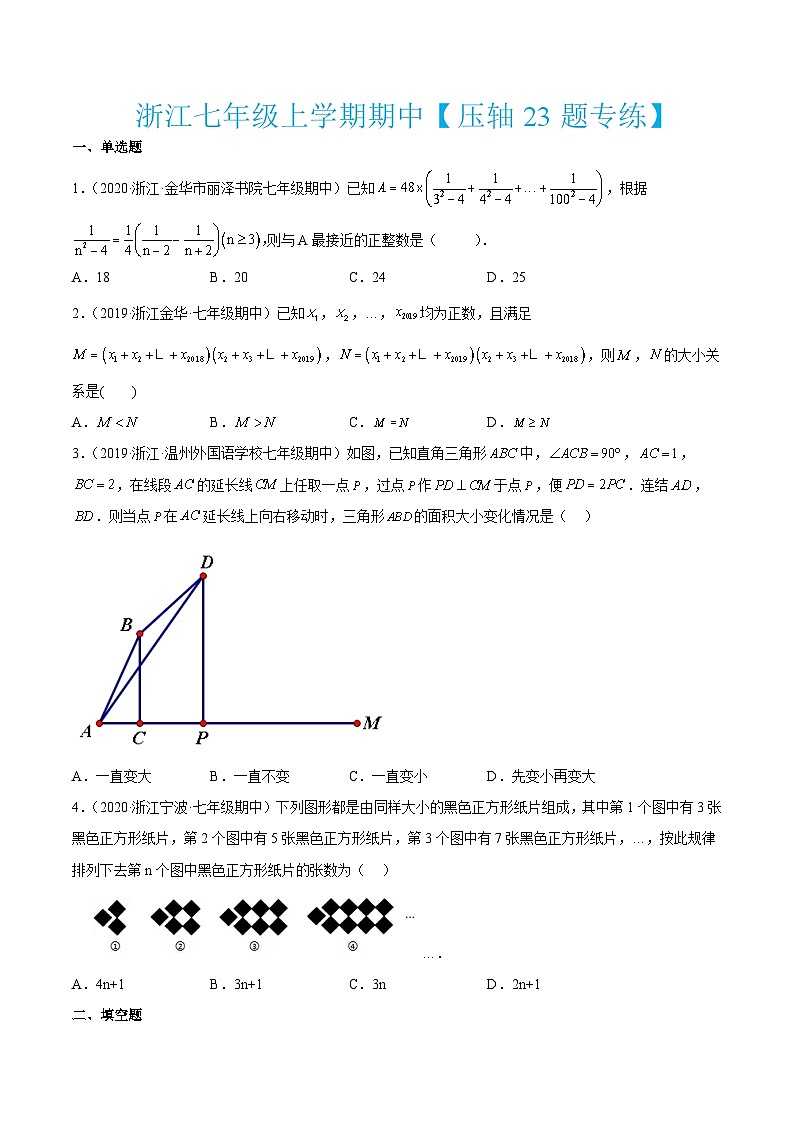
1．（2020·浙江·金华市丽泽书院七年级期中）已知，根据则与A最接近的正整数是（ ）．
A．18B．20C．24D．25
【答案】D
【分析】根据公式的特点把A进行变形化简，故可求解．
【详解】∵
∴
=
≈12×2.0435=24.522≈25
故选：D．
【点睛】此题主要考查数的规律计算，解题的关键是运用已知的运算公式变形求解．
2．（2019·浙江金华·七年级期中）已知，，…，均为正数，且满足，，则，的大小关系是( )
A．B．C．D．
【答案】B
【分析】设，，然后求出MN的值，再与0进行比较即可.
【详解】解：根据题意，设，，
∴，
∴；
；
∴
=
=；
∴；
故选：B.
【点睛】本题考查了比较实数的大小，以及数字规律性问题，解题的关键是熟练掌握作差法比较大小.
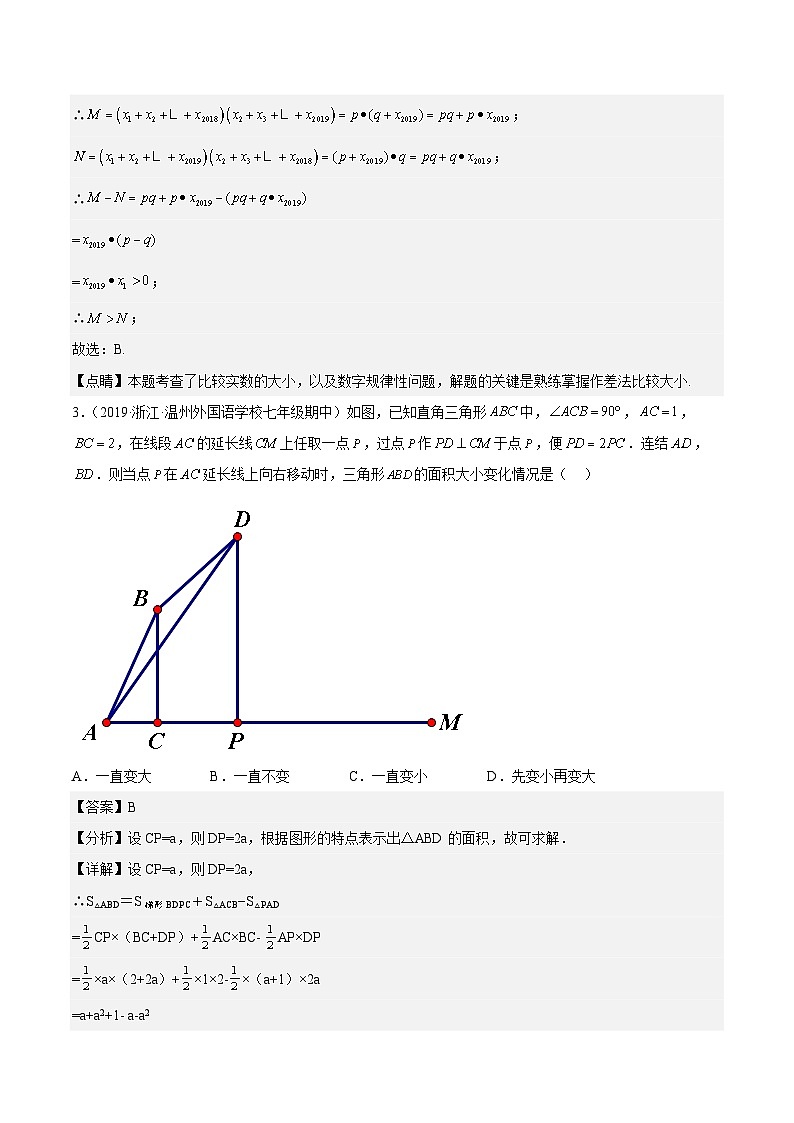
3．（2019·浙江·温州外国语学校七年级期中）如图，已知直角三角形中，，，，在线段的延长线上任取一点，过点作于点，便．连结，．则当点在延长线上向右移动时，三角形的面积大小变化情况是（ ）
A．一直变大B．一直不变C．一直变小D．先变小再变大
【答案】B
【分析】设CP=a，则DP=2a，根据图形的特点表示出△ABD的面积，故可求解．
【详解】设CP=a，则DP=2a，
∴S△ABD＝S梯形BDPC＋S△ACB−S△PAD
=CP×（BC+DP）+AC×BC-AP×DP
=×a×（2+2a）+×1×2-×（a+1）×2a
=a+a2+1- a-a2
=1
∴三角形的面积大小不变
故选B．
【点睛】此题主要考查列代数式，解题的关键是熟知三角形及梯形的面积求解．
4．（2020·浙江宁波·七年级期中）下列图形都是由同样大小的黑色正方形纸片组成，其中第1个图中有3张黑色正方形纸片，第2个图中有5张黑色正方形纸片，第3个图中有7张黑色正方形纸片，…，按此规律排列下去第n个图中黑色正方形纸片的张数为（ ）
…．
A．4n+1B．3n+1C．3nD．2n+1
【答案】D
【分析】根据图形的规律可知，从第二个图形开始，每个图形中的黑色正方形纸片数比前一个图形多2个，由此可推出结果．
【详解】第1个图中有3张黑色正方形纸片，
第2个图中有5张黑色正方形纸片，
第3个图中有7张黑色正方形纸片，
…，
依次类推，第n个图中黑色正方形纸片的张数为2n+1，
故选：D．
【点睛】本题考查了图形的规律，代数式表示图形的个数，掌握图形的规律是解题的关键．
二、填空题
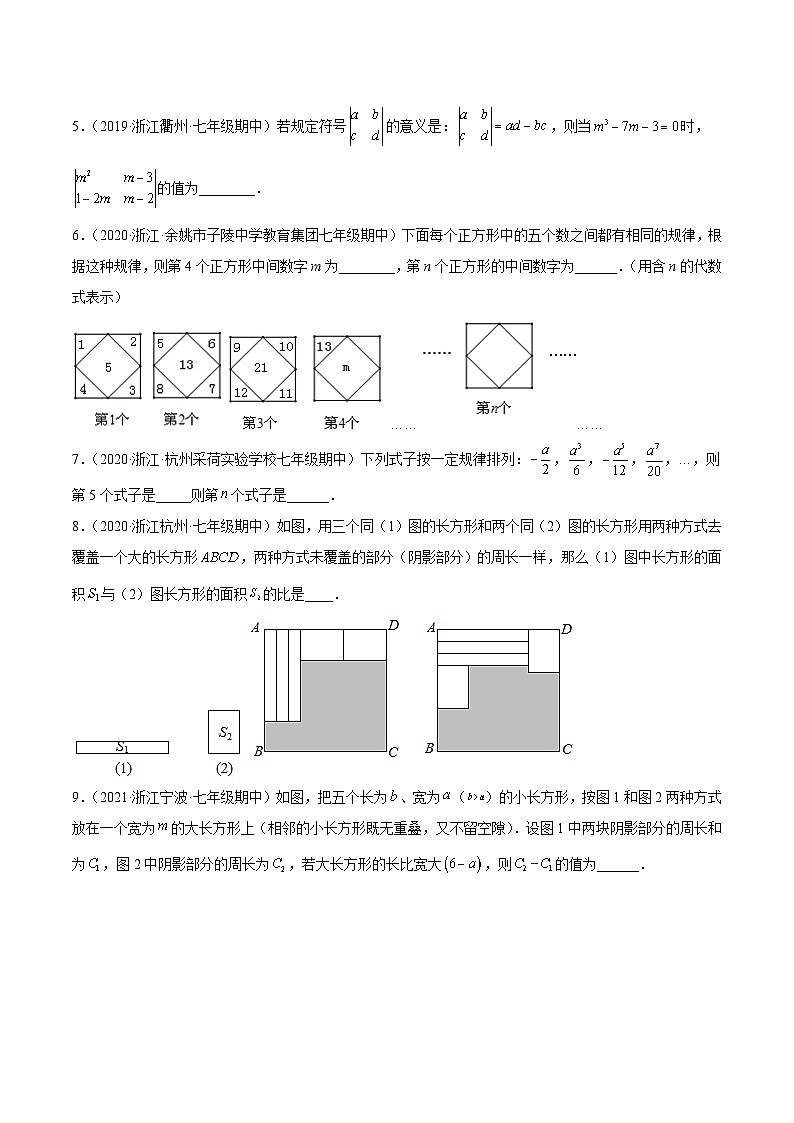
5．（2019·浙江衢州·七年级期中）若规定符号的意义是：，则当时，的值为________．
【答案】
【分析】根据定义的新运算的运算法则，得出的值，然后进行化简，最后再整体代入即可求值．
【详解】
∵，
∴，
∴原式=．
故答案为：6．
【点睛】本题主要考查定义新运算，掌握多项式的乘法法则和整体代入法是解题的关键．
6．（2020·浙江·余姚市子陵中学教育集团七年级期中）下面每个正方形中的五个数之间都有相同的规律，根据这种规律，则第4个正方形中间数字m为________，第n个正方形的中间数字为______．（用含n的代数式表示）
…………
【答案】 29
【分析】由前三个正方形可知：右上和右下两个数的和等于中间的数，根据这一个规律即可得出m的值；首先求得第n个的最小数为1+4（n-1）=4n-3，其它三个分别为4n-2，4n-1，4n，由以上规律即可求解．
【详解】解：由题知：右上和右下两个数的和等于中间的数，
∴第4个正方形中间的数字m=14+15=29；
∵第n个的最小数为1+4（n-1）=4n-3，其它三个分别为4n-2，4n-1，4n，
∴第n个正方形的中间数字：4n-2+4n-1=8n-3．
故答案为：29；8n-3
【点睛】本题主要考查的是图形的变化规律，通过观察、分析、归纳发现数字之间的运算规律是解题的关键．
7．（2020·浙江·杭州采荷实验学校七年级期中）下列式子按一定规律排列：，，，，…，则第5个式子是_____则第个式子是______．
【答案】
【分析】根据符号的规律是奇数项为负，偶数项为正，分母的规律是2=1×2，6=2×3，12=3×4，20=4×5，…，分子的规律是底数为a，指数是1，3，5，7，…，即可解答．
【详解】解：由，，，，…，可知符号的规律是奇数项为负，偶数项为正，分母的规律是2=1×2，6=2×3，12=3×4，20=4×5，…，分子的规律是底数为a，指数是1，3，5，7，…，
∴第5个式子是，
第个式子是，
故答案为：，．
【点睛】本题考查数字规律，解题的关键是根据题意找出单项式之间的规律，本题属于基础题型．
8．（2020·浙江杭州·七年级期中）如图，用三个同（1）图的长方形和两个同（2）图的长方形用两种方式去覆盖一个大的长方形，两种方式未覆盖的部分（阴影部分）的周长一样，那么（1）图中长方形的面积与（2）图长方形的面积的比是____．
【答案】
【分析】本题需先设图（1）中长方形的长为acm，宽为bcm，图（2）中长方形的宽为xcm，长为ycm，再结合图形分别得出图形（3）的阴影周长和图形（4）的阴影周长，相等后列等式可得：a＝2y，x＝3b，最后根据长方形面积公式可得结论．
【详解】解：设图（1）中长方形的长为acm，宽为bcm，图（2）中长方形的宽为xcm，长为ycm，
由两个长方形ABCD的AD＝3b＋2y＝a＋x，

∴图（3）阴影部分周长为：2（3b＋2y＋DC−x）＝6b＋4y＋2DC−2x＝2a＋2x＋2DC−2x＝2a＋2DC，
∴图（4）阴影部分周长为：2（a＋x＋DC−3b）＝2a＋2x＋2DC−6b＝2a＋2x＋2DC−2（a＋x−2y）＝2DC＋4y，

∵两种方式未覆盖的部分（阴影部分）的周长一样，
∴2a＋2DC＝2DC＋4y，a＝2y，
∵3b＋2y＝a＋x，
∴x＝3b，
∴S1：S2＝ab：xy＝2yb：3yb＝，
故答案是：．
【点睛】本题主要考查了整式的加减运算，根据题意结合图形得出3b＋2y＝a＋x ，2a＋2DC＝2DC＋4y是解题的关键．
9．（2021·浙江宁波·七年级期中）如图，把五个长为、宽为（）的小长方形，按图1和图2两种方式放在一个宽为的大长方形上（相邻的小长方形既无重叠，又不留空隙）．设图1中两块阴影部分的周长和为，图2中阴影部分的周长为，若大长方形的长比宽大，则的值为______．

【答案】12
【分析】先将图1拆成两个长方形，分别算出两个长方形的长和宽即可求出；将图2的每条边长都求出来，相加即可求出；再根据两个长方形的长相等得到等式，用和表示，代入中即可得出答案.
【详解】由图可知
∴
又
∴
故答案为12.
【点睛】本题考查的是整式的加减，解题的关键是理解题意得出等式.
10．（2020·浙江·金华市丽泽书院七年级期中）黑板上写有1，，，，…，共100个数字，每次操作先从黑板上的数中选取2个数a，b，然后删去a，b，并在黑板上写上数a+b+1，则经过_____次操作后，黑板上只剩下一个数，这个数是_____．
【答案】 99
【分析】将所给数化为＝1﹣，＝﹣，＝﹣，…，＝﹣，再根据题意可知，在操作的过程中，这100个数都要求和，操作99次后剩余一个数，则可得黑板最后剩下的是+99＝．
【详解】解：＝1﹣，＝﹣，＝﹣，…，＝﹣，
每次取两个数a，b，删去a，b，并在黑板上写上数a+b+1，
∵这100个数的和是1++++…+=1+1﹣﹣﹣﹣＝2﹣＝，
则黑板上的数求和后，每次再加1，
每次都是去掉2个数，添加一个数，故黑板最后剩一个数，则操作99次，
∴黑板最后剩下的是+99＝．
故答案为：99；．
【点睛】本题考查数字的变化规律以及有理数的加法等知识，理解题意并将所给式子进行拆项相加是解题的关键．
11．（2020·浙江·杭州采荷实验学校七年级期中）代数式，当时，可化简为______；若代数式的最大值为与最小值为，则的值______．
【答案】 3 -9
【分析】当时，可得x-1＜0，x+2＜0，利用绝对值的性质即可化简，分别化简当时以及当x＞1时，根据当时，，求出a，b即可．
【详解】解：当时，x-1＜0，x+2＜0，
∴，
当时，，
当x＞1时，
∵当时，，
∴代数式的最大值为3，最小值为-3，
∴a=3，b=-3，
∴ab=-9，
故答案为：3，-9．
【点睛】本题主要考查了绝对值的化简，解题的关键是对x进行分类讨论，再化简代数式．
12．（2021·浙江·七年级期中）设，，，…；另设，，，…．已知是一个关于的三次多项式（为正整数），可表示为，则________．
【答案】1
【分析】由N1=n1=1,那么令n=1代入即可解答．
【详解】解：∵N1=n1=1
∴令k=1，则有：N1==a+b+c+d
∴a+b+c+d=1．
故填1．
【点睛】本题属于竞赛题，主要考查了特殊值法的应用，发现N1=n1=1,是解答本题的关键．
13．（2020·浙江·永嘉县上塘城关中学七年级期中）已知整数，，，，…，满足下列条件：，，，，，，…，依次类推，则的值为______．
【答案】
【分析】根据题意计算出、、、、、，发现规律即可求解．
【详解】∵，
∴=；
；
=；
；
；
……四组一循环
根据规律可知=
故答案为：-2021．
【点睛】此题主要考查实数变化的规律探究，解题的关键是根据题意写出前几个数，发现规律求解．
三、解答题
14．（2020·浙江·温州市第十二中学七年级期中）阅读材料：
对于排好顺序的三个数：，称为数列．计算的值，将这三个算式的最小值称为数列的价值．例如，对于数列，因为，所以数列的价值为．
当改变数列中三个数的顺序时，所得到的数列都可以按照上述方法计算其相应的价值.如数列的价值为，数列的价值等等．对于“”这三个数，按照不同的排列顺序得到的不同数列中，价值的最小值为．
根据以上材料，回答下列问题：
（1）求数列的价值；
（2）将“”这三个数按照不同的顺序排列，可得若干个数列，求取得的价值最小时的数列．
（3）已知，将“”这三个数按照不同的顺序排列，可得若干个数列，若这些数列的价值的最小值为1，求的值．
【答案】（1）数列的价值是2；（2）数列为：3，-2，5；或-2，3，5时，数列的价值的最小值为；（3）a的值为1或11或5．
【分析】（1）根据定义，代入直接可求；
（2）数列共6中排列方式，分别求出每一种情况的价值，即可求解；
（3）分和和和四种情况讨论，分别求解并判断即可．
【详解】解：（1）因为，
所以，数列的价值是2；
（2）由（1）得数列的价值是2；
因为，故数列的价值是；
因为，故数列3，-2，5的价值是；
因为，故数列3，5，-2的价值是2；
因为，故数列-2，5，3的价值是；
因为，故数列-2，3，5的价值是；
数列为：3，-2，5；或-2，3，5时，数列的价值的最小值为；
（3）因为
故当时，因为，所以；
当时，（舍去）或（舍去）
当时，或，当时，，故不符合题意舍去；
当时，或，当时，，故不符合题意舍去；
综上所述a的值为1或11或5．
【点睛】本题考查数字的规律，新定义．理解题意，利用绝对值的性质计算是解题的关键．
15．（2020·浙江·杭州采荷实验学校七年级期中）已知数轴上三点对应的数分别为，3，点为数轴上任意一点，其对应的数为。
（1）三点中，其中一个点是另外两个点连成的线段的中点（把一条线段分成相等部分的点），那么的值是_________．
（2）数轴上是否存在点，使点到点，点的距离之和是7？若存在，请直接写出的值；若不存在，请说明理由．
（3）如果点以每分钟3个单位长度的速度从原点向右运动时，点和点分别以每分钟4个单位长度和每分钟1个单位长度的速度也向右运动，且三点同时出发，那么几分钟后，三点中，其中一个点是另外两个点连成的线段的中点
【答案】（1）1或-5或7；（2）的值为或；（3）经过2分钟或分钟或分钟后
【分析】（1）对点P的位置进行分类讨论，利用数轴上两点之间的距离列出方程即可解答；
（2）由题意得：|x-(-1)|+|x-3|=7，再对x的取值进行分类讨论即可解答；
（3）表达出t分钟后，点M，N，P表示的数，再对M，N，P三点的位置进行分类讨论，利用数轴上两点之间的距离列出方程即可解答．
【详解】解：（1）①若点P是线段MN的中点，则MP=NP，
即x-(-1)=3-x，解得：x=1，
②若点M是线段PN的中点，则PM=MN，
即-1-x=3-(-1)，解得：x=-5，
③若点N是线段PM的中点，则PN=MN，
即x-3=3-(-1)，解得：x=7，
故答案为：1或-5或7；
（2）由题意得：|x-(-1)|+|x-3|=7，
①当点x＜-1时，|x-(-1)|+|x-3|=-(x+1)-(x-3)
即-(x+1)-(x-3)=7，解得：x=，
②当-1≤x≤3时，|x-(-1)|+|x-3|=x+1-(x-3)，
即x+1-(x-3)=7，方程无解，
③当x＞3时，|x-(-1)|+|x-3|=x+1+x-3
即x+1+x-3=7，解得：x=，
综上所述，的值为或；
（3）设时间为t分钟，则t分钟后，点M，N，P表示的数分别为：-1+4t，3+t，3t，
①若点P是线段MN的中点，则MP=NP，
则3t-(-1+4t)=3+t-3t，解得：t=2，
②若点M是线段PN的中点，则PM=MN，
则-1+4t-3t=3+t-(-1+4t)，解得：t=，
③若点N是线段PM的中点，则PN=MN，
则3+t-3t=-1+4t-(3+t)，解得：t=，
综上所述，经过2分钟或分钟或分钟后，三点中，其中一个点是另外两个点连成的线段的中点．
【点睛】本题主要考查数轴和一元一次方程的应用，解答本题的关键是根据数轴和路程问题，列出一元一次方程求解，注意分情况讨论，不要漏解．
16．（2020·浙江·七年级期中）如图，某快递员要从公司点A出发，前往B、C、D等地派发包裹，规定：向上向右走为正，向下向左走为负，并且行走方向顺序为先左右再上下．如果从A到B记为：A→B（＋1，＋4），从B到A记为：B→A（－1，－4），其中第一个数表示左右方向，第二个数表示上下方向，请根据图完成如下问题：
（1）A→C（ ， ），B→D（ ， ），C→D（＋1， ）；
（2）若快递员的行走路线为A→B→C→D，请计算该快递员走过的路程；
（3）若快递员从A处去某P处的行走路线依次为（＋2，＋2），（＋1，－1），（－2，＋3），（－1，－2），请在图中标出P的位置．
【答案】（1）；（2）10；（3）图见解析．
【分析】（1）参考从A到B的记作方法即可得；
（2）先分别求出A→B、B→C、C→D，再将相应数字的绝对值求和即可得；
（3）根据题意中的规定方法和记作方法逐个路线分析即可得．
【详解】（1）：先向右走3单位长度，再向上走4单位长度，则，
：先向右走3单位长度，再向下走2单位长度，则，
：先向右走1单位长度，再向下走2单位长度，则；
（2）因为，
所以快递员按所行走的路程为，
，
；
（3）快递员到达图中的E处，
快递员到达图中的F处，
快递员到达图中的B处，
快递员到达图中的P处，
则P处的位置如图所示：
【点睛】本题考查了正负数在实际生活中的应用、绝对值运算，读懂题干中的规定和记作方法是解题关键．
17．（2020·浙江·杭州市朝晖中学七年级期中）阅读绝对值拓展材料：表示数a在数轴上的对应点与原点的距离如：表示5在数轴上的对应点到原点的距离而，即表示5、0在数轴上对应的两点之间的距离，类似的，有：表示5、在数轴上对应的两点之间的距离．一般地，点A、B在数轴上分别表示有理数a、b，那么A、B之间的距离可表示为．
回答下列问题：
（1）数轴上表示2和5的两点之间的距离是 ，数轴上表示1和的两点之间的距离是 ；
（2）数轴上表示x和的两点A和B之间的距离是 ，如果A、B两点之间的距离为2，那么 ．
（3）可以理解为数轴上表示x和 的两点之间的距离．
（4）可以理解为数轴上表示x的点到表示 和 这两点的距离之和．可以理解为数轴上表示x的点到表示 和 这两点的距离之和．
（5）最小值是 ，的最小值是 ．
【答案】（1）3，4；（2）|x+1|，x=1或-3；（3）-2；（4）2，3，-2，1；（5）1，3
【分析】（1）根据两点之间的距离公式计算即可；
（2）根据两点之间的距离公式计算即可；
（3）根据绝对值的意义可得；
（4）根据绝对值的意义可得；
（5）分别得出和的意义，再根据数轴的性质可得．
【详解】解：（1）数轴上表示2和5的两点之间的距离是3，
数轴上表示1和-3的两点之间的距离是4；
（2）数轴上表示x和-1的两点A和B之间的距离是|x+1|，
如果|AB|=2，即|x+1|=2，
∴x=1或-3；
（3）|x+2|可以理解为数轴上表示x和-2的两点之间的距离；
（4）|x-2|+|x-3|可以理解为数轴上表示x的点到表示2和3这两点的距离之和，
|x+2|+|x-1|可以理解为数轴上表示x的点到表示-2和1这两点的距离之和；
（5）由（4）可知：
当x在2和3之间时，|x-2|+|x-3|最小值是1，
当x在-2和1之间时，|x+2|+|x-1|的最小值是3．
【点睛】本题考查的是绝对值的问题，涉及到数轴应用问题，只要理解绝对值含义和数轴上表示数值的关系（如：|x+2|表示x与-2的距离），即可求解．
18．（2020·浙江·宁波市第七中学七年级期中）如图，点、在数轴上分别表示实数、，、两点之间的距离表示为，在数轴上、两点之间的距离请你利用数轴回答下列问题：
（1）数轴上表示2和6两点之间的距离是________，数轴上表示1和的两点之间的距离为________．
（2）数轴上表示和1两点之间的距离为_______，数轴上表示和两点之间的距离为________．
（3）若表示一个实数，且，化简________．
（4）的最小值为________．
（5）的最大值为________．
【答案】（1）4，3；（2）|x-1|，|x+3|；（3）8；（4）6；（5）4
【分析】（1）（2）直接代入公式即可；
（3）实质是在点表示3和-5的点之间取一点，计算该点到点3和-5的距离和；
（4）可知x对应点在3时，|x-1|+|x-2|+|x-3|+|x-4|+|x-5|值最小；
（5）分当-1＜x＜3时，当x≤-1时，当x≥3时，三种情况分别化简，从而求出最大值．
【详解】解：（1）|6-2|=4，|-2-1|=3，
答案为：4，3；
（2）根据两点间距离公式可知：数轴上表示x和1两点之间的距离为|x-1|，
数轴上表示x和-3两点之间的距离为|x+3|，
故答案为：|x-1|，|x+3|；
（3）x对应点在点-5和3之间时的任意一点时|x-3|+|x+5|的值都是8，
故答案为：8；
（4）|x-1|+|x-2|+|x-3|+|x-4|+|x-5|表示数x到1，2，3，4，5的距离之和，
可知：当x对应点是3时，|x-1|+|x-2|+|x-3|+|x-4|+|x-5|的最小值为6，
故答案为：6；
（5）当-1＜x＜3时，|x+1|-|x-3|=x+1+x-3=2x-2，
-4＜2x-2＜4，
当x≤-1时，|x+1|-|x-3|=-x-1+x-3=-4，
当x≥3时，|x+1|-|x-3|=x+1-x+3=4，
综上：的最大值为4．
【点睛】此题主要考查了绝对值、数轴等知识，用几何方法借助数轴来求解，非常直观，体现了数形结合的优点．
19．（2020·浙江·宁波市镇海区尚志中学七年级期中）如果把一个自然数各数位上的数字从最高位到个位依次排出的一串数字，与从个位到最高位依次排出的一串数字完全相同，那么我们把这样的自然数称为“和谐数”．例如自然数12321，从最高位到个位依次排出的一串数字是：1，2，3，2，1，从个位到最高位依次排出的一串数字仍是：1，2，3，2，1，因此12321是一个“和谐数”．再如22，545，3883，345543，…，都是“和谐数”．
（1）请你直接写出2个四位“和谐数”，并猜想任意一个四位“和谐数”能否被11整除？并说明理由．
（2）已知一个能被11整除的三位“和谐数”，设其个位上的数字是（，为自然数），十位上的数字是，用含的代数式表示．
【答案】（1），（答案不唯一）；任意一个四位“和谐数”都能被11整除，理由见解析；（2）．
【分析】（1）根据“和谐数”的定义即可得；设一个四位“和谐数”为，先根据“和谐数”的定义可得，再根据十进制、整式的加减可得这个四位数为，由此即可得；
（2）设这个能被11整除的三位“和谐数”为，先根据“和谐数”的定义可得，再根据十进制、整式的加减可得这个三位数为，从而可得是整数，然后根据的取值范围可得，由此即可得出答案．
【详解】（1）由“和谐数”的定义得：，是“和谐数”（答案不唯一），
任意一个四位“和谐数”都能被11整除，理由如下：
设一个四位“和谐数”为，
则最高位到个位的排列为，
个位到最高位的排列为，
由“和谐数”的定义得：，
则这个四位“和谐数”为，
，
，
，
因此，任意一个四位“和谐数”都能被11整除；
（2）由题意，设这个能被11整除的三位“和谐数”为，
则最高位到个位的排列为，
个位到最高位的排列为，
由“和谐数”的定义得：，
则这个三位“和谐数”为，
，
，
能被11整除，均为整数，
是整数，
是整数，
又，
，
要使是整数，则的取值只能是0，
即，
故．
【点睛】本题考查了整式加减的应用、列代数式，正确理解“和谐数”的定义是解题关键．
20．（2020·浙江·七年级期中）定义：若A，B，C为数轴上三点，若点C到点A的距离是点C到点B的距离2倍，我们就称点C是的美好点．
例如；如图1，点A表示的数为，点B表示的数为2．表示1的点C到点A的距离是2，到点B的距离是1，那么点C是的美好点；又如，表示0的点D到点A的距离是1，到点B的距高是2，那么点D就不是的美好点，但点D是的美好点．
如图2，M，N为数轴上两点，点M所表示的数为，点N所表示的数为2．
（1）点E，F，G表示的数分别是，6.5，11，其中是美好点的是________；写出美好点H所表示的数是___________．
（2）现有一只电子蚂蚁P从点N开始出发，以2个单位每秒的速度向左运动．当t为何值时，点P恰好为M和N的美好点？
【答案】（1）G，-4或-16；（2）1.5或3或9
【分析】（1）根据美好点的定义，结合图2，直观考察点E，F，G到点M，N的距离，只有点G符合条件．结合图2，根据美好点的定义，在数轴上寻找到点N的距离是到点M的距离2倍的点，在点的移动过程中注意到两个点的距离的变化．
（2）根据美好点的定义，分情况分别确定P点的位置，进而可确定t的值．
【详解】解：（1）根据美好点的定义，结合图2，直观考察点E，F，G到点M，N的距离，只有点G符合条件，
故答案是：G．
结合图2，根据美好点的定义，在数轴上寻找到点N的距离是到点M的距离2倍的点，点N的右侧不存在满足条件的点，点M和N之间靠近点M一侧应该有满足条件的点，进而可以确定-4符合条件．点M的左侧距离点M的距离等于点M和点N的距离的点符合条件，进而可得符合条件的点是-16．
故答案是：-4或-16．
（2）根据美好点的定义，P，M和N中恰有一个点为其余两点的美好点分6种情况，
第一情况：当P为【M，N】的美好点，点P在M，N之间，如图1，
当MP=2PN时，PN=3，点P对应的数为2-3=-1，因此t=1.5秒；
第二种情况，当P为【N，M】的美好点，点P在M，N之间，如图2，
当2PM=PN时，NP=6，点P对应的数为2-6=-4，因此t=3秒；
第三种情况，P为【N，M】的美好点，点P在M左侧，如图3，
当PN=2MN时，NP=18，点P对应的数为2-18=-16，因此t=9秒；
综上所述，t的值为：1.5或3或9．
【点睛】本题考查实数与数轴、美好点的定义等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考创新题目．
21．（2019·浙江·台州市书生中学七年级期中）已知：b是最小的正整数，且a、b满足＋＝0，请回答问题：
（1）请直接写出a、b、c的值；
（2）数轴上a、b、c所对应的点分别为A、B、C，点M是A、B之间的一个动点，其对应的数为m，请化简（请写出化简过程）；
（3）在（1）（2）的条件下，点A、B、C开始在数轴上运动．若点A以每秒1个单位长度的速度向左运动．同时，点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动．假设t秒钟过后，若点B与点C之间的距离表示为BC，点A与点B之间的距离表示为AB．请问：BC－AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值．
【答案】（1）-1；1；5；（2）①当m