初中数学沪教版（五四制）（2024）七年级下册第十四章 三角形第2节 全等三角形14.4 全等三角形的判定同步练习题

这是一份初中数学沪教版（五四制）（2024）七年级下册第十四章 三角形第2节 全等三角形14.4 全等三角形的判定同步练习题，文件包含沪教版数学七年级下册同步讲练第10讲全等三角形的判定与性质及应用原卷版doc、沪教版数学七年级下册同步讲练第10讲全等三角形的判定与性质及应用解析版doc等2份试卷配套教学资源，其中试卷共75页， 欢迎下载使用。
一．全等三角形的判定与性质
（1）全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．
（2）在应用全等三角形的判定时，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形．
二．全等三角形的应用
（1）全等三角形的性质与判定综合应用
用全等寻找下一个全等三角形的条件，全等的性质和判定往往是综合在一起应用的，这需要认真分析题目的已知和求证，分清问题中已知的线段和角与所证明的线段或角之间的联系．
（2）作辅助线构造全等三角形
常见的辅助线做法：①把三角形一边的中线延长，把分散条件集中到同一个三角形中是解决中线问题的基本规律．②证明一条线段等于两条线段的和，可采用“截长法”或“补短法”，这些问题经常用到全等三角形来证明．
（3）全等三角形在实际问题中的应用
一般方法是把实际问题先转化为数学问题，再转化为三角形问题，其中，画出示意图，把已知条件转化为三角形中的边角关系是关键．
一．全等三角形的判定与性质（共9小题）
1．（2020秋•宝山区校级期末）已知：如图，点A、B、C、D在同一条直线上，AB＝DC，AE∥DF，AE＝DF，求证：EC＝FB．
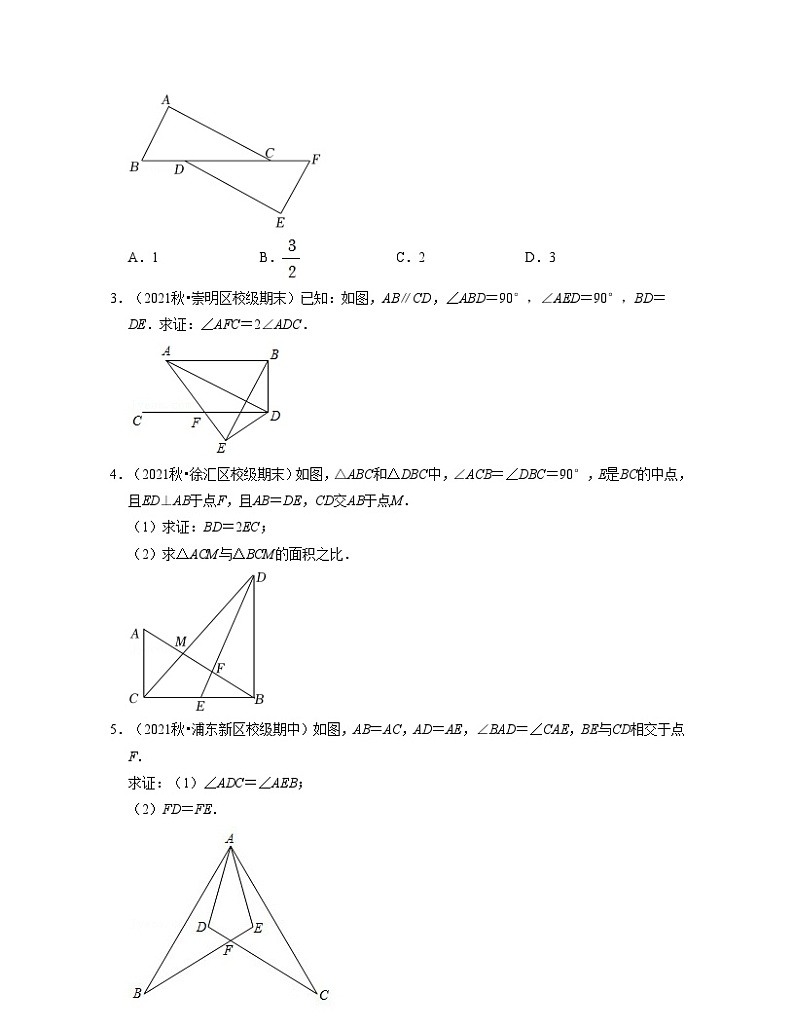
2．（2021秋•普陀区期末）如图，已知点B、D、C、F在同一条直线上，AB∥EF，AB＝EF，AC∥DE，如果BF＝6，DC＝3，那么BD的长等于（ ）
A．1B．C．2D．3
3．（2021秋•崇明区校级期末）已知：如图，AB∥CD，∠ABD＝90°，∠AED＝90°，BD＝DE．求证：∠AFC＝2∠ADC．
4．（2021秋•徐汇区校级期末）如图，△ABC和△DBC中，∠ACB＝∠DBC＝90°，E是BC的中点，且ED⊥AB于点F，且AB＝DE，CD交AB于点M．
（1）求证：BD＝2EC；
（2）求△ACM与△BCM的面积之比．
5．（2021秋•浦东新区校级期中）如图，AB＝AC，AD＝AE，∠BAD＝∠CAE，BE与CD相交于点F．
求证：（1）∠ADC＝∠AEB；
（2）FD＝FE．
6．（2021秋•徐汇区校级期中）已知在△ABC中，AB＝AC，在边AC上取一点D，以D为顶点，DB为一条边作∠BDF＝∠A，点E在AC的延长线上，∠ECF＝∠ACB．
求证：（1）∠FDC＝∠ABD；
（2）DB＝DF；
（3）当点D在AC延长线上时，DB＝DF是否依然成立？在备用图中画出图形，并说明理由．
7．（2021春•金山区期末）阅读并填空：如图，已知在△ABC中，AB＝AC，点D、E在边BC上，且AD＝AE，说明BD＝CE的理由．
解：因为AB＝AC，
所以 ；（等边对等角）
因为 ，（已知）
所以∠AED＝∠ADE；（等边对等角）
因为∠AED＝∠EAC+∠C，
∠ADE＝∠BAD+∠B，（ ）
所以∠BAD＝∠EAC；（等式性质）
在△ABD与△ACE中，
所以△ABD≌△ACE（A．S．A）
所以 ．（全等三角形的对应边相等）
8．（2021秋•松江区期末）在△ABC中，AD是BC边上的中线，AD⊥AB，如果AC＝5，AD＝2，那么AB的长是 ．
9．（2021秋•普陀区期末）已知：如图，在△ABC中，AB＝CB，∠ABC＝45°，高AD与高BE相交于点F，G为BF的中点．
求证：（1）DG＝DE；
（2）∠DEG＝∠DEC．
二．全等三角形的应用（共3小题）
10．（2021春•金山区期末）如图，有两根钢条AB、CD，在中点O处以小转轴连在一起做成工具（卡钳），可测量工件内槽的宽．如果测量AC＝2cm，那么工件内槽的宽BD＝ cm．
11．（2020春•嘉定区期末）如图，两车从路段MN的两端同时出发，以相同的速度行驶，相同时间后分别到达A，B两地，两车行进的路线平行．那么A，B两地到路段MN的距离相等吗？为什么？
12．（2019春•嘉定区期末）如图，两车从路段A，B的两端同时出发，以相同的速度行驶，相同时间后分别到达C，D两地，两车行进的路线平行．那么C，D两地到路段AB的距离相等吗？为什么？
分层提分
题组A 基础过关练
一．选择题（共3小题）
1．（2016秋•天津期末）小明不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有1、2、3、4的四块），你认为将其中的哪一些块带去，就能配一块与原来一样大小的三角形？应该带（ ）
A．第1块B．第2块C．第3块D．第4块
2．（2015•义乌市）如图，小敏做了一个角平分仪ABCD，其中AB＝AD，BC＝DC．将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A，C画一条射线AE，AE就是∠PRQ的平分线．此角平分仪的画图原理是：根据仪器结构，可得△ABC≌△ADC，这样就有∠QAE＝∠PAE．则说明这两个三角形全等的依据是（ ）
A．SASB．ASAC．AASD．SSS
3．（2021秋•营山县期中）在△ABC中，AB＝5，AC＝7，AD是BC边上的中线，则AD的取值范围是（ ）
A．0＜AD＜12B．1＜AD＜6C．0＜AD＜6D．2＜AD＜12
二．填空题（共10小题）
4．（2021秋•沂水县期中）如图，点B、E、C、F在同一条直线上，AB∥DE，AB＝DE，∠A＝∠D，BF＝10，BC＝6，则EC＝ ．
5．（2021春•杨浦区期末）在△ABC与△DEF中，∠A＝∠D，∠B＝∠E，BC＝EF，AB＝3cm，AC＝5cm，那么DE＝ cm．
6．（2015秋•蒙城县期末）如图所示，将两根钢条AA′，BB′的中点O连在一起，使AA′，BB′可以绕着点O自由转动，就做成了一个测量工具，则A′B′的长等于内槽宽AB，那么判定△OAB≌△OA′B′的理由是 ．
7．（2009•杨浦区二模）如图所示，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是带 去玻璃店．
8．（2021秋•普陀区期中）如图，△ABC中，AD⊥BC于点D，BE⊥AC于点E，AD、BE相交于点F，如果BF＝AC，BC＝8，CD＝2，那么AF＝ ．
9．（2021秋•徐汇区校级月考）如图，△ABC的周长为26，点D、E都在边BC上，∠ABC的平分线垂直于AE，垂足为Q，∠ACB的平分线垂直于AD，垂足为P，若BC＝10，则DE的长是 ．
10．（2021秋•徐汇区校级月考）△ABC中，AB＝6，AC＝8，点D是BC边上的中点，则AD的取值范围是 ．
11．（2021春•盐湖区校级期末）在△ABC中，AB＝AC，点D是△ABC外一点，连接AD、BD、CD，且BD交AC于点O，在BD上取一点E，使得AE＝AD，∠EAD＝∠BAC，若∠ACB＝70°，则∠BDC的度数为 ．
12．（2021秋•长沙期中）如图，∠ACB＝90°，AC＝BC，BE⊥CE，AD⊥CE，垂足分别为E，D，AD＝25，DE＝17，则BE＝ ．
13．（2021秋•梅里斯区期末）小明不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有1、2、3、4的四块），你认为将其中的哪一块带去，就能配一块与原来一样大小的三角形？应该带第 块．
三．解答题（共15小题）
14．（2021春•黄浦区期末）如图，点A、B、C、D在一条直线上如果AC＝BD，BE＝CF，且BE∥CF，那么AE∥DF．为什么？
解：∵BE∥CF（已知），
∴∠EBC＝∠FCB（ ）．
∵∠EBC+∠EBA＝180°，∠FCB+∠FCD＝180°（平角的意义），
∴∠EBA＝∠FCD（ ）．
∵AC＝BD（已知），
∴AC﹣BC＝BD﹣BC（等式性质），
即 ．（完成以下说理过程）
15．（2021秋•徐汇区校级期中）已知，如图，△ABC中，∠C＝90°，D是AB上一点，DE⊥CD于D，交BC于E，且有AC＝AD＝CE，求证：DE＝CD．
16．（2020春•普陀区期末）如图，已知AB＝DE，AC＝DF，BF＝EC．
（1）说明△ABC与△DEF全等的理由；
（2）如果AC＝CF，∠1＝30°，∠D＝105°，求∠AFC的度数．
17．（2019秋•徐汇区校级月考）如图，在△ABC中，BD平分∠ABC，M、N分别是BA、BC上的点，且∠MDN+∠MBN＝180°，求证：DM＝DN．
18．（2021春•浦东新区月考）如图所示，在△ABC中，AD是∠BAC的平分线，M是BC的中点，MF∥DA交BA的延长线于点E，交AC于点F，求证：BE＝CF．
19．（2021春•闵行区期末）如图，已知在等腰△ABC中AB＝AC，点D，点E和点F分别是BC，AB和AC边上的点，且BE＝DC，∠B＝∠EDF，试说明DE＝DF．
20．（2021春•闵行区期末）如图，△ABC中，AD⊥BC，垂足为点D，CE⊥AB，垂足为点E，AD＝DC，CE和AD交于点F，联结BF，试说明∠FBD＝45°．
21．（2021春•浦东新区校级期末）如图，已知∠B＝∠C＝90°，AE⊥ED，AB＝EC，EF⊥AD，试说明点F是AD的中点的理由．
22．（2021春•浦东新区期末）如图，在三角形ABC中，已知点D、E、F分别在边BC、AC、AB上，且FD＝DE，BF＝CD，∠FDE＝∠B，那么∠B与∠C相等吗？为什么？
23．（2021春•浦东新区期末）如图，在△ABC中，点D是边BC的中点，过点C作直线CE，使CE∥AB，交AD的延长线于点E．试说明AD＝ED的理由．
解：因为CE∥AB（已知），
所以∠BAD＝ （ ）．
因为点D是边BC的中点，
所以 ，
在△ABD和△ECD中，
，
所以△ABD≌△ECD（ ），
所以AD＝ED（ ）．
24．（2021春•黄浦区期末）如图在四边形ABCD中，AD∥BC，E是AB的中点，连接DE并延长交CB的延长线于点F，点G在边BC上，且∠1＝∠2．
（1）说明△ADE≌△BFE的理由；
（2）联结EG，那么EG与DF的位置关系是 ，请说明理由．
25．（2021春•杨浦区期末）如图，已知△ABC与△BDE都是等边三角形，点D在边AC上，说明CE∥AB的理由．
解：因为△ABC是等边三角形（已知），
所以∠A＝∠ABC＝60°，AB＝BC（等边三角形的意义）．
因为△BDE是等边三角形（已知），
所以∠BE＝60°，BD＝BE（等边三角形的意义）．
所以∠ABC﹣∠DBC＝∠DBE﹣∠DBC（等式性质），
得∠ABD＝ ．
在△ABD与△CBE中，，
所以△ABD≌△CBE（ ）．
所以∠A＝ （ ）．
又因为∠A＝∠ABC，
所以∠ABC＝ （等量代换）．
所以CE∥AB（ ）．
26．（2021春•杨浦区期末）如图，已知△ADE≌△CBF，顶点A、D、E分别与顶点C、B、F对应，据此可以判断图中有哪几组直线互相平行？请说明理由．
27．（2021春•普陀区校级期中）如图，在△ABC中，点D、E分别在BC、AB上，AE＝AC，过点E作EF∥BC交AC于F，EC平分∠DEF．说明∠BAD＝∠CAD．
28．（2021春•浦东新区校级期末）如图，已知∠A＝∠B，AE＝BE，点D在AC边上，∠1＝∠2，AE和BD相交于点O．
（1）求证：△AEC≌△BED；
（2）若∠1＝44°，求∠BDE的度数．
题组B 能力提升练
一．填空题（共2小题）
1．（2021秋•浦东新区期中）如图，已知AD是△ABC的中线，E是AC上的一点，BE交AD于F，AC＝BF，∠DAC＝24°，∠EBC＝32°，则∠ACB＝ ．
2．（2021春•黄浦区期末）如图，△ABC中，AB＝AC，BD＝CE，BE＝CF，若∠A＝50°，则∠DEF的度数是 ．
二．解答题（共15小题）
3．（2021秋•徐汇区校级月考）如图，四边形ABCD中，BC＝CD，CB⊥AB于B，CD⊥AD于D，求证：AB＝AD．
4．（2021春•浦东新区校级期末）如图，在四边形ABCD中，AB∥CD，∠1＝∠2，AD＝EC．则线段AB，BE，CD之间存在怎样的数量关系？并说明理由．
5．（2021春•静安区期末）如图，已知四边形ABCD中，AB∥CD，AD∥BC．E为BD上一点，且BE＝AD，∠DEF＝∠ADC，EF交BC的延长线于点F．
（1）AD和BC相等吗？为什么？
（2）BF和BD相等吗？为什么？
6．（2020秋•奉贤区期末）已知：在△ABC中，AB＝6，AC＝5，△ABC的面积为9．点P为边AB上动点，过点B作BD∥AC，交CP的延长线于点D．∠ACP的平分线交AB于点E．
（1）如图1，当CD⊥AB时，求PA的长；
（2）如图2，当点E为AB的中点时，请猜想并证明：线段AC、CD、DB的数量关系．
7．（2020春•虹口区期中）如图，已知E、F是BD上的两点，BE＝DF，AE＝CF，AE∥CF，请填写AD∥BC的理由．
解：因为AE∥CF（已知），
所以∠AED＝ （两直线平行，内错角相等）．
因为BE＝DF（已知），
所以BE+EF＝DF+EF（ ），
即BF＝DE．
在△ADE与△CBF中
，
所以△ADE≌△CBF（ ）．
得∠ADE＝∠CBF（ ）．
所以AD∥BC（ ）．
8．（2020秋•普陀区期中）如图，已知AB＝AC，BD＝CD，过点D作DE⊥AB交AB的延长线于点E、DF⊥AC交AC的延长线于点F，垂足分别为点E、F．
（1）求证：∠DBE＝∠DCF．
（2）求证：BE＝CF．
9．（2019秋•浦东新区期末）已知：如图，△ABC中，∠ABC＝45°，AD⊥BC，BE⊥AC于D，垂足分别为点D、E，AD与BE相交于点F．求证：DF＝DC．
10．（2019春•青浦区期末）如图，点A、B、C、D在一条直线上．如果AC＝BD，BE＝CF，且BE∥CF，那么AE∥DF．为什么？
解：因为BE∥CF（已知），所以∠EBC＝∠FCB（ ）．
因为∠EBC+∠EB4＝180°，∠FCB+∠FCD＝180°（平角的意义），所以 （ ）．
因为AC＝BD（已知），所以AC﹣BC＝BD﹣BC（等式性质），即 （完成以下说理过程）．
11．（2019春•奉贤区期末）阅读并填空：
如图，△ABC是等腰三角形，AB＝AC，D是边AC延长线上的一点，E在边AB上，且联接DE交BC于O，如果OE＝OD，那么CD＝BE，为什么？
解：过点E作EF∥AC交BC于F，
所以∠ACB＝∠EFB（两直线平行，同位角相等），
∠D＝∠OEF（ ），
在△OCD与△OFE中，
，
所以△OCD≌OFE，（ ），
所以CD＝FE（ ），
因为AB＝AC（已知），
所以∠ACB＝∠B（ ），
所以∠EFB＝∠B（等量代换），
所以BE＝FE，
所以CD＝BE．
12．（2019秋•浦东新区期中）在等腰△OAB和等腰△OCD中，OA＝OB，OC＝OD，连接AC、BD交于点M．
（1）如图1，若∠AOB＝∠COD＝40°：
①AC与BD的数量关系为 ；
②∠AMB的度数为 ．
（2）如图2，若∠AOB＝∠COD＝90°：
①判断AC与BD之间存在怎样的数量关系？并说明理由；
②求∠AMB的度数．
13．（2018秋•松江区期末）在△ABC中，点Q是BC边上的中点，过点A作与线段BC相交的直线l，过点B作BN⊥l于N，过点C作CM⊥l于M．
（1）如图1，如果直线l过点Q，求证：QM＝QN；
（2）如图2，若直线l不经过点Q，联结QM，QN，那么第（1）问的结论是否成立？若成立，给出证明过程；若不成立，请说明理由．
14．（2018秋•金山区期末）已知：如图，A、F、C、D在同一直线上，AB∥DE，AB＝DE，AF＝CD，
求证（1）BC＝EF；
（2）BC∥EF．
15．（2021秋•浦东新区期中）如图1，在△ABC中，∠A＝120°，∠C＝20°，BD平分∠ABC，交AC于点D．
（1）求证：BD＝CD．
（2）如图2，若∠BAC的角平分线AE交BC于点E，求证：AB+BE＝AC．
（3）如图3，若∠BAC的外角平分线AE交CB的延长线于点E，则（2）中的结论是否成立？若成立，给出证明，若不成立，写出正确的结论．
16．（2021春•浦东新区期末）如图，在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＝∠DAE＝90°．
（1）当点D在AC上时，如图①，线段BD，CE有怎样的数量关系和位置关系？请证明你的猜想；
（2）将图①中的△ADE绕点A顺时针旋转α（0°＜α＜90°），如图②，线段BD，CE有怎样的数量关系和位置关系？请说明理由．
17．（2014春•金堂县期末）一条大河两岸的A、B处分别立着高压线铁塔，如图所示．假设河的两岸平行，你在河的南岸，请利用现有的自然条件、皮尺和标杆，并结合你学过的全等三角形的知识，设计一个不过河便能测量河的宽度的好办法．（要求，画出示意图，并标出字母，结合图形简要叙述你的方案）