





备战2025年高考数学精品课件第二章 第8讲 函数模型的应用
展开
这是一份备战2025年高考数学精品课件第二章 第8讲 函数模型的应用,共59页。PPT课件主要包含了给出下列四个结论,①②③,ABD,ACD等内容,欢迎下载使用。
1. 几种常见的函数模型
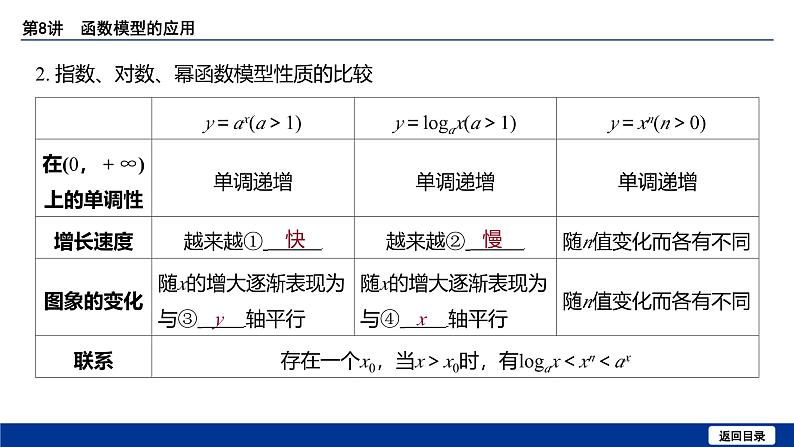
2. 指数、对数、幂函数模型性质的比较
1. 下列说法正确的是( D )
2. 已知 f ( x )= x 2, g ( x )=2 x , h ( x )=lg2 x ,当 x ∈(4,+∞)时,对三个函数的增
长速度进行比较,下列选项中正确的是( B )
4. [2023湖南省株洲市模拟]“每天进步一点点”可以用数学来诠释,假如你今天的
数学水平是1,以后每天比前一天增加千分之五,则经过 y 天之后,你的数学水平 x
与 y 之间的函数关系式是( C )
①在[ t 1, t 2]这段时间内,甲企业的污水治理能力比乙企业强;
②在 t 2时刻,甲企业的污水治理能力比乙企业强;
③在 t 3时刻,甲、乙两企业的污水排放都已达标;
④甲企业在[0, t 1],[ t 1, t 2],[ t 2, t 3]这三段时间中,在[0, t 1]的污水治
理能力最强.
其中所有正确结论的序号是 .
[解析] 由题图可知甲企业的污水排放量在 t 1时刻高于乙企业,而在 t 2时刻甲、乙
两企业的污水排放量相同,故在[ t 1, t 2]这段时间内,甲企业的污水治理能力比乙
企业强,故①正确;甲企业污水排放量与时间的关系图象在 t 2时刻切线的斜率的绝
对值大于乙企业,故②正确;在 t 3时刻,甲、乙两企业的污水排放量都低于污水达
标排放量,故都已达标,③正确;甲企业在[0, t 1],[ t 1, t 2],[ t 2, t 3]这三段时间
中,在[ t 1, t 2]这段时间的污水治理能力最强,故④错误.
方法技巧判断函数图象与实际变化过程是否吻合的方法(1)构建函数模型法:若易构建函数模型,则先建立函数模型,再结合模型选择函数
图象.(2)验证法:根据实际问题中两变量的变化快慢等特点,结合函数图象的变化趋势,
验证是否吻合,从中排除不符合实际的情况,选择出符合实际情况的答案.
命题点2 已知函数模型求解实际问题
例2 (1)[2024武汉部分学校调考]某企业在生产中为倡导绿色环保的理念,购入污水
过滤系统对污水进行过滤处理,已知在过滤过程中污水中的剩余污染物数量 N
(mg/L)与时间 t (h)的关系为 N = N 0e- kt ,其中 N 0为初始污染物的数量, k 为常数.若
在某次过滤过程中,前2个小时过滤掉了污染物的30%,则可计算前6个小时共能过
滤掉污染物的( C )
已知在距离燃油汽车、混合动力汽车、电动汽车10 m处测得实际声压分别为 p 1, p 2, p 3,则( ACD )
方法技巧已知函数模型求解实际问题的步骤(1)认清所给函数模型,弄清哪些量为待定系数;(2)根据已知利用待定系数法,确定模型中的待定系数;(3)利用该函数模型,借助函数的性质、导数等求解实际问题,并进行检验.
命题点3 构造函数模型求解实际问题例3 (1)[2024四川省叙永一中模拟]净水机通过分级过滤的方式使自来水逐步达到纯
净水的标准,其中第一级过滤一般由孔径为5微米的 PP 棉滤芯(聚丙烯熔喷滤芯)构
成,其结构是多层式的,主要用于去除铁锈、泥沙、悬浮物等各种大颗粒杂质,假
设每一层 PP 棉滤芯可以过滤掉三分之一的大颗粒杂质,若过滤前水中大颗粒杂质
含量为80 mg/L,现要满足过滤后水中大颗粒杂质含量不超过2 mg/L,则 PP 棉滤芯
的层数最少为(参考数据:lg 2≈0.301,lg 3≈0.477)( A )
(2)[2023南昌市模拟]某市出台两套出租车计价方案,方案一:2千米及2千米以内收
费8元(起步价),超过2千米的部分每千米收费3元,不足1千米按1千米计算;方案
二:3千米及3千米以内收费12元(起步价),超过3千米不超过10千米的部分每千米收
费2.5元,超过10千米的部分每千米收费3.5元,不足1千米按1千米计算.以下说法正
确的是( C )
方法技巧构建函数模型解决实际问题的步骤(1)建模:抽象出实际问题的数学模型;(2)推理、演算:对数学模型进行逻辑推理或数学运算,得到问题在数学意义上
的解;(3)评价、解释:对求得的数学结果进行深入讨论,作出评价、解释,返回到原来的
实际问题中去,得到实际问题的解.
2. [命题点2/多选]第31届世界大学生夏季运动会在四川成都举行,大运会吉祥物“蓉
宝”备受人们欢迎.某大型超市举行抽奖活动,推出“单次消费满1 000元可参加抽
奖”的活动,奖品为若干个大运会吉祥物“蓉宝”.抽奖结果分为五个等级,等级 x
与获得“蓉宝”的个数 f ( x )的关系式为 f ( x )= p +e kx + b ,已知三等奖比四等奖获得
的“蓉宝”多2个,比五等奖获得的“蓉宝”多3个,且三等奖获得的“蓉宝”数是
五等奖的2倍,则( ABD )
3. [命题点3]某省2023年退休人员基本养老金,采取定额调整、挂钩调整和适当倾斜
相结合的办法.(1)定额调整:每人每月增加41元养老金.(2)挂钩调整:按以下两部分
计算增加养老金,①按2022年12月本人基本养老金的1.25%确定月增加额;②按本
人缴费年限分段确定月增加额,其中,对15年(含)以下的部分,每满1年,月增加1.2
元,16年(含)以上至25年的部分,每满1年,月增加1.4元,26年(含)以上至35年的部
分,每满1年,月增加1.6元,36年(含)以上至45年的部分,每满1年,月增加1.8元,
46年(含)以上的部分,每满1年,月增加2元.(3)适当倾斜:2022年12月31日前,年满
70周岁不满75周岁、年满75周岁不满80周岁和年满80周岁的退休人员,每人每月分
别增加15元、30元和60元养老金.张女士今年57周岁,缴费年限是34年,2022年12月
的基本养老金为3 000元,则张女士2023年基本养老金的月增加额为( B )
[解析] 张女士年龄不满70周岁,没有“适当倾斜”的部分,只有定额调整41元和挂钩调整的两部分,其中按2022年12月本人基本养老金的1.25%确定的月增加额为3 000×1.25%=37.5(元);按本人缴费年限分段确定的月增加额为15×1.2+10×1.4+(34-15-10)×1.6=46.4(元).因此张女士2023年基本养老金的月增加额为41+37.5+46.4=124.9(元),故选B.
1. [2023合肥市二检]Malthus模型是一种重要的数学模型.某研究人员在研究一种细菌
数量 N ( t )与时间 t 的关系时,得到的Malthus模型是 N ( t )= N 0e0.46 t ,其中 N 0是 t = t 0时刻的细菌数量,e为自然对数的底数.若 t 时刻细菌数量是 t 0时刻细菌数量的6.3倍,则 t 约为(ln 6.3≈1.84)( C )
[解析] 因为 t 时刻细菌数量是 t 0时刻细菌数量的6.3倍,所以 N 0e0.46 t =6.3 N 0,即
e0.46 t =6.3,则0.46 t =ln 6.3≈1.84,得 t ≈4.故选C.
3. [2022北京高考]在北京冬奥会上,国家速滑馆“冰丝带”使用高效环保的二氧化
碳跨临界直冷制冰技术,为实现绿色冬奥作出了贡献.如图描述了一定条件下二氧化
碳所处的状态与 T 和lg P 的关系,其中 T 表示温度,单位是K; P 表示压强,单位是
bar .下列结论中正确的是( D )
[解析] 对于A选项,当 T =220, P =1 026,即lg P =lg 1 026>lg 103=3
时,根据图象可知,二氧化碳处于固态;对于B选项,当 T =270, P =128,
即lg P =lg 128∈(lg102,lg103),即lg P ∈(2,3)时,根据图象可知,二氧化
碳处于液态;对于C选项,当 T =300, P =9 987,即lg P =lg 9 987<lg104
=4时,根据图象可知,二氧化碳处于固态;对于D选项,当 T =360, P =
729,即lg P =lg 729∈(lg102,lg103),即lg P =lg 729∈(2,3)时,根据图象
可知,二氧化碳处于超临界状态.故选D.
4. [多选/2024广东七校联考]尽管目前人类还无法准确预报地震,但科学家经过研
究,已经对地震有所了解,例如,地震时释放的能量 E (单位:焦耳)与地震里氏震
级 M 之间的关系为lg E =4.8+1.5 M ,则下列说法正确的是( ACD )
5. [2024江苏常州模拟]牛顿曾经提出了常温环境下的温度冷却模型:θ=(θ1-θ0)e- kt
+θ0,其中 t 为时间(单位:min),θ0为环境温度,θ1为物体初始温度,θ为冷却后温
度.假设在室内温度为20°C的情况下,一杯饮料由100 ℃降低到60 ℃需要20 min,则
此饮料从60 ℃降低到25 ℃需要 min .
(1)当投入 A , B 两个项目的资金相同且 B 项目比 A 项目一年创造的利润高时,求投
入 A 项目的资金 x (单位:万元)的取值范围.
综上,投入 A 项目的资金 x (单位:万元)的取值范围为(10,40).
(2)若该公司共有资金30万,全部用于投资 A , B 两个项目,则该公司一年分别投入
A , B 两个项目多少万元时,创造的总利润最大?
8. [2024江苏省南京市第九中学模拟]天宫空间站的轨道高度为400~450千米,倾角
为42~43度,设计寿命为10年,长期驻留3人,总质量可达180吨,以进行较大规模
的空间应用.某项实验在空间站进行,实验开始时,某物质的含量为1.2 mg/cm3,每
经过1小时,该物质的含量就会减少20%,若该物质的含量不超过0.2 mg/cm3,则实
验进入第二阶段,那么实验进入第二阶段至少需要(需要的小时数取整数,参考数
据:lg 2≈0.30,lg 3≈0.48)( B )
10. [2024河北省衡水市第十三中学模拟]为进一步奏响“绿水青山就是金山银山”的
主旋律,某旅游风景区以“绿水青山”为主题,特别制作了旅游纪念章,并决定近
期投放市场.根据市场调研情况,预计每枚纪念章的市场价 y (单位:元)与上市时间 x
(单位:天)的数据如下表
(2)记你所选取的函数 y = f ( x ),若对任意 x ∈[ k ,+∞)( k >0),不等式 kf ( x )-32 k
-210≥0恒成立,求实数 k 的取值范围.
相关课件
这是一份第14讲 函数模型及其应用高考数学复习课件,共60页。PPT课件主要包含了第二单元函数,教师备用习题,作业手册等内容,欢迎下载使用。
这是一份2025年高考数学一轮复习-第二章 函数-第9讲 函数模型及应用【课件】,共40页。PPT课件主要包含了必备知识自主排查,核心考点师生共研等内容,欢迎下载使用。
这是一份高考数学一轮复习第二章第九讲函数模型及其应用课件,共36页。PPT课件主要包含了常见的函数模型,选择数学模型,常用结论,图2-9-1,答案B,答案D,图2-9-2,的特点故选B,种方法,Cln2等内容,欢迎下载使用。




![《高考总复习》数学 第二章 第14讲 函数模型及其应用[配套课件]](http://jx-previews-01.oss-cn-hangzhou.aliyuncs.com/3/3/13744187/0/0.jpg?x-oss-process=image/resize,w_202)




