






备战2025年高考数学精品课件第五章 突破2 数列中的构造问题
展开
这是一份备战2025年高考数学精品课件第五章 突破2 数列中的构造问题,共35页。PPT课件主要包含了n-1,n+1,命题拓展,方法技巧,n+2,ABD,步骤如下,BCD等内容,欢迎下载使用。
命题点1 形如 an +1= pan + f ( n )( p ≠1)
例1 (1)在数列{ an }中, a 1=1, an +1=3 an -2 n -1,则 an = .
(2)设数列{ an }满足 a 1=3, an +1=3 an -4 n ,则 an = .
[解析] 由已知可得 an +1-(2 n +3)=3[ an -(2 n +1)], an -(2 n +1)=3[ an -1-(2 n -1)],…, a 2-5=3( a 1-3).因为 a 1=3,所以 an =2 n +1.
[变条件]若例1(2)中的 a 1=4,则 an = .
[解析] 设 an +1+ x ( n +1)+ y =3( an + xn + y ),则展开利用对应项系数相等可得
出 x =-2, y =-1,所以{ an -2 n -1}是以 a 1-2-1=1为首项,3为公比的等比
数列,所以 an -2 n -1=3 n -1,所以 an =3 n -1+2 n +1.
3 n -1+2 n +1
形如 an +1= pan + f ( n )( p ≠1)的递推式,一般采用构造法求通项:
(1)若 f ( n )为非零常数,则一般凑配成 an +1+ x = p ( an + x )的形式(利用待定系数法
求 x ),构造等比数列;
(2)若 f ( n )为关于 n 的一次函数,则一般凑配成 an +1+ x ( n +1)+ y = p ( an + xn + y )
的形式(利用待定系数法求 x , y ),构造等比数列;
(3)若 f ( n )为指数幂(如 qn )的形式,则一般两边同时除以 pn +1或 qn +1,再利用累加法
或构造法求通项.
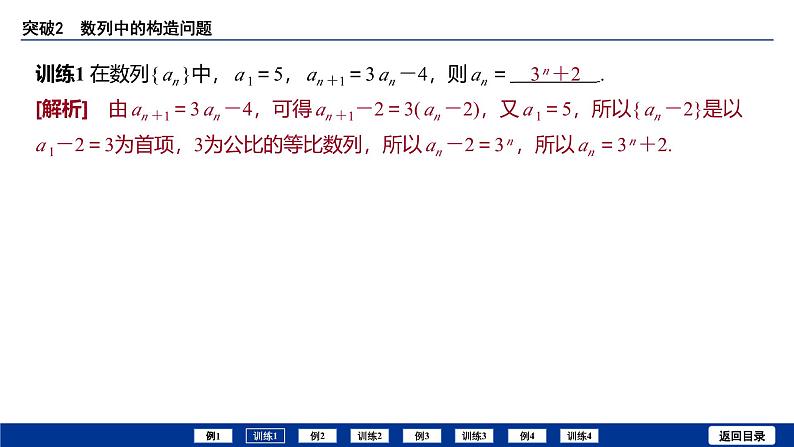
训练1 在数列{ an }中, a 1=5, an +1=3 an -4,则 an = .
[解析] 由 an +1=3 an -4,可得 an +1-2=3( an -2),又 a 1=5,所以{ an -2}是以 a 1-2=3为首项,3为公比的等比数列,所以 an -2=3 n ,所以 an =3 n +2.
命题点3 形如 an +1= pan + qan -1( n ≥2)
例3 已知数列{ an }满足 an +1=5 an -6 an -1( n ≥2),且 a 1=1, a 2=4,则数列{ an }
的通项公式为 .
an =2×3 n -1-2 n -1
形如 an +1= pan + qan -1( n ≥2)的递推式,一般采用构造法求通项,将原式变形为 an +1+λ an =μ( an +λ an -1)( n ≥2),由待定系数法求出λ,μ,再依据相邻两项的递推
关系求通项.
训练3 已知数列{ an }满足 a 1=1, a 2=2,且对任意 n ∈N*,都有 an +2=3 an +1-2 an .则{ an }的通项公式为 .
an =2 n -1
思维帮·提升思维 快速解题
用“不动点法”求数列的通项公式
利用不动点法求数列通项的步骤
对于一个函数 f ( x ),我们把满足 f ( m )= m 的值 m 称为函数 f ( x )的“不动点”.利用
“不动点法”可以构造新数列,求数列的通项公式.
iii.解方程得出 an .
3. [2024河南焦作统考]已知数列{ an }满足 an +1=3 an +2, a 3+ a 2=22,则满足 an
>160的最小正整数 n = .
4. [2023合肥六中三模]已知在数列{ an }中, a 1=5, a 2=2, an =2 an -1+3 an -2( n
≥3),则数列{ an }的通项公式为 .
[解析] ∵ an =2 an -1+3 an -2( n ≥3),∴ an + an -1=3( an -1+ an -2)( n ≥3),又 a 1
+ a 2=7,∴{ an +1+ an }是首项为7,公比为3的等比数列,则 an +1+ an =7×3 n -1
7. [2024名师原创]设数列{ an }的前 n 项和为 Sn ,满足2 Sn = an +1-2 n +1+1( n
∈N*),且 a 1, a 2+5, a 3成等差数列.
(1)求 a 1的值;
[解析] (1)2 Sn = an +1-2 n +1+1,令 n =2得2 S 2= a 3-23+1,即2 a 1+2 a 2= a 3-7 ①.因为 a 1, a 2+5, a 3成等差数列,所以2( a 2+5)= a 1+ a 3,即 a 3=2( a 2+5)- a 1
②,将②代入①可得2 a 1+2 a 2=2( a 2+5)- a 1-7,解得 a 1=1,故 a 1的值为1.
(2)求数列{ an }的通项公式.
8. [2024浙江宁波模拟]已知数列{ an }满足 a 1=1,且对任意正整数 m , n 都有 am + n
= an + am +2 mn .
(1)求数列{ an }的通项公式;
相关课件
这是一份备战2025年高考数学精品课件第五章 第2讲 等差数列,共60页。PPT课件主要包含了一个常数,等差中项,规律总结,等差数列的单调性,等差数列的性质,最小公倍数,方法技巧,BCD,A15,B30等内容,欢迎下载使用。
这是一份备战2025年高考数学精品课件第五章 突破3 数列中的创新型问题,共32页。PPT课件主要包含了ABD,故选B等内容,欢迎下载使用。
这是一份备战2025年高考数学精品课件第八章 突破2 圆锥曲线中的最值、范围问题,共37页。PPT课件主要包含了1求p等内容,欢迎下载使用。








