重庆市长寿实验中学2024-2025学年八年级上学期第一次月考数学试卷

这是一份重庆市长寿实验中学2024-2025学年八年级上学期第一次月考数学试卷，共31页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（3分）下列等式中，从左到右的变形是因式分解的是（ ）
A．x2+2x+3＝x（x+2）+3B．（x+1）2＝x2+2x+1
C．D．x2﹣4＝（x+2）（x﹣2）
2．（3分）下列长度的三条线段首尾顺次相接能组成三角形是（ ）
A．1，2，3B．2，4，7C．3，4，8D．2，3，4
3．（3分）下列多边形中，内角和与外角和相等的是（ ）
A．B．
C．D．
4．（3分）下列计算中正确的是（ ）
A．（x2）2＝x5B．x3﹣x2＝x
C．（a﹣b）2＝a2﹣b2D．﹣x2•x＝﹣x3
5．（3分）2022年2月8日上午，谷爱凌在女子滑雪大跳台决赛中，获得了北京冬奥会雪上项目的首金．如图所示，大跳台的∠B＝35°，∠C＝y°，∠BAD＝x°，请找出y与x的关系式（ ）
A．y＝145﹣xB．y＝x﹣35C．y＝x+55D．y＝x+35
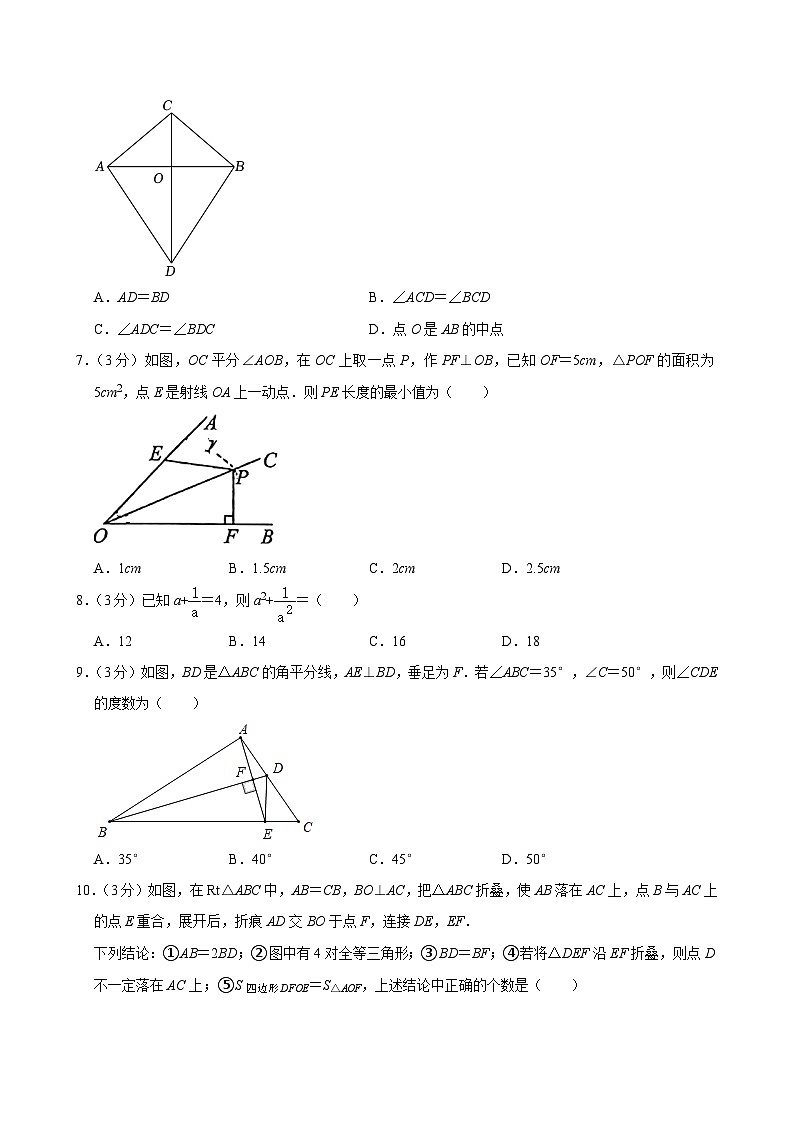
6．（3分）如图，AC＝BC，下列条件不能判定△ACD与△BCD全等的是（ ）
A．AD＝BDB．∠ACD＝∠BCD
C．∠ADC＝∠BDCD．点O是AB的中点
7．（3分）如图，OC平分∠AOB，在OC上取一点P，作PF⊥OB，已知OF＝5cm，△POF的面积为5cm2，点E是射线OA上一动点．则PE长度的最小值为（ ）
A．1cmB．1.5cmC．2cmD．2.5cm
8．（3分）已知a+＝4，则a2+＝（ ）
A．12B．14C．16D．18
9．（3分）如图，BD是△ABC的角平分线，AE⊥BD，垂足为F．若∠ABC＝35°，∠C＝50°，则∠CDE的度数为（ ）
A．35°B．40°C．45°D．50°
10．（3分）如图，在Rt△ABC中，AB＝CB，BO⊥AC，把△ABC折叠，使AB落在AC上，点B与AC上的点E重合，展开后，折痕AD交BO于点F，连接DE，EF．
下列结论：①AB＝2BD；②图中有4对全等三角形；③BD＝BF；④若将△DEF沿EF折叠，则点D不一定落在AC上；⑤S四边形DFOE＝S△AOF，上述结论中正确的个数是（ ）
A．1B．2C．3D．4
二、填空题
11．（3分）计算：2m2•（3m）2＝ ．
12．（3分）若992﹣1＝ ．
13．（3分）若多项式x2+（m﹣1）x+9是一个完全平方式，则m的值是 ．
14．（3分）如图，AD⊥BC于点D，D为BC的中点，连接AB，∠ABC的平分线交AD于点O，连接OC，若∠AOC＝120°，则∠ABC＝ ．
15．（3分）如图，在RT△ABC中，∠ACB＝90°，AC＝BC，直角顶点C在y轴上，点A在x轴上，OC＝2OA＝4，则点B的坐标为 ．
16．（3分）若关于x的不等式组，有且只有3个整数解，且关于y的一元一次方程2y+6＝3a的解是正整数，则所有满足条件的整数a的值之和为 ．
17．（3分）下列说法：
①已知a，b，c满足a2+6a+b2﹣4b+c2﹣2c+14＝0，则a+b+c＝0；
②已知a，b，c是正整数，a＞b，且a2﹣（b﹣c）2＝5，则a＝3，b＝2，c＝4；
③若实数x，y，m满足2x+y+m＝5，3x+2y+m＝8，则代数式3xy﹣1的值可以是6．
其中正确的是 （请在横线上填写序号）．
三、解答题：
18．计算：
（1）5x（x+2y﹣8）；
（2）（3x+2y）（﹣2y+3x）．
19．因式分解：
（1）24a3bc2﹣8ab2；
（2）（m+3n）（4m﹣n）﹣（m+3n）（m﹣7n）．
20．如图，点D在线段BC上，AB∥CE，AB＝CD，BD＝CE．
（1）求作∠ADE的平分线，并交AE于点F（要求：尺规作图，保留作图痕迹，不写作法）；
（2）在（1）问的条件下试证明：AF＝EF，请将以下推导过程补充完整．
证明：∵AB∥CE，
∴∠B＝∠C．
在△ABD和△DCE中
，
∴△ABD≌△DCE（ ），
∴ ．
∵DF平分∠ADE，
∴∠ADF＝∠EDF．
在△ADF和△EDF中
，
∴△ADF≌△EDF（SAS），
∴AF＝EF．
21．先化简，再求值：[（a﹣b）2﹣2b（a﹣b）﹣（a+b）（a﹣b）]÷（﹣4b），其中a＝1，b＝．
22．为深入学习贯彻党的二十大精神，引领广大职工准确把握党的二十大报告的丰富内涵、精神实质、实践要求，江北区教育工会开展了学习二十大知识竞赛活动，根据竞赛活动的成绩划分了四个等级：A：合格，B：良好，C：优秀，D：非常优秀．现随机抽查部分竞赛成绩的数据进行了整理、绘制成部分统计图：
请根据图中信息，解答下列问题：
（1）填空：a＝ ，“优秀”对应扇形的圆心角度数为 ；
（2）请你补全条形统计图；
（3）若我区有8000名教职工，请你估计其中“优秀”和“非常优秀”的教职工共有多少人？
23．如图，点E在CD上，BC与AE交于点F，AB＝CB，BE＝BD，∠1＝∠2．
（1）求证：△ABE≌△CBD；
（2）若∠2＝55°，求∠3的度数．
24．为改善校园环境，提升办学品质，重庆市鲁能巴蜀中学计划拆除网球场，新建综合大楼．已知2辆甲型除渣车和3辆乙型除渣车每天可以除渣170吨，3辆甲型除渣车和2辆乙型除渣车每天可以除渣180吨．
（1）求甲、乙两种型号的除渣车每辆每天分别可以除渣多少吨？
（2）施工期间，学校决定租赁甲、乙两种型号的除渣车共20辆，已知每辆甲型除渣车租赁价格为15万元，每辆乙型除渣车租赁价格为12万元，要想使租赁除渣车的总费用不超过261万元，且每天除渣总量又不低于650吨，请你求出所有的租赁方案．
25．数学活动课中，老师给出以下问题：
（1）如图1，在△ABC中，D是边BC的中点，若AB＝5，AC＝9，则中线AD长度的取值范围 ．
（2）如图2，在△ABC中，D是边BC的中点，过D点的射线DE交边AB于E，再作DF⊥DE交边AC于点F，连接EF，请探索由三条线段BE、EF、CF构成的三角形的形状，并说明理由．
（3）已知：如图3，AB＝AC，∠BAC＝∠CDE＝90°，且DC＝DE，F是线段BE的中点．求证：AF⊥FD．
26．现有长与宽分别为a、b的小长方形若干个，用两个这样的小长方形拼成如图1的图形，用四个相同的小长方形拼成图2的图形，请认真观察图形，解答下列问题：
（1）根据图中条件，请写出图1和图2所验证的关于a、b的关系式：（用含a、b的代数式表示出来）；
图1表示： ；
图2表示： ；
根据上面的解题思路与方法，解决下列问题：
（2）若x+y＝8，x2+y2＝40，求xy的值；
（3）请直接写出下列问题答案：
①若2m+3n＝5，mn＝1，则2m﹣3n＝ ；
②若（4﹣m）（5﹣m）＝6，则（4﹣m）2+（5﹣m）2＝ ．
（4）如图3，点C是线段AB上的一点，以AC，BC为边向两边作正方形，设AB＝7，两正方形的面积和S1+S2＝16，求图中阴影部分面积．
2024-2025学年重庆市长寿实验中学八年级（上）第一次月考数学试卷
参考答案与试题解析
一、选择题
1．（3分）下列等式中，从左到右的变形是因式分解的是（ ）
A．x2+2x+3＝x（x+2）+3B．（x+1）2＝x2+2x+1
C．D．x2﹣4＝（x+2）（x﹣2）
【分析】根据因式分解的定义“将多项式化为几个整式的积的形式”，由此即可求解．
【解答】解：A、不是因式分解，不符合题意；
B、不是因式分解，不符合题意；
C、等号右边不是整式，不是因式分解，不符合题意；
D、是因式分解，符合题意；
故选：D．
【点评】本题主要考查因式分解的概念，掌握其概念是解题的关键．
2．（3分）下列长度的三条线段首尾顺次相接能组成三角形是（ ）
A．1，2，3B．2，4，7C．3，4，8D．2，3，4
【分析】根据三角形的三边关系：任意两边的和一定大于第三边，即两个短边的和大于最长的边，即可进行判断．
【解答】解：A、1+2＝3，故不能构成三角形，故此选项不符合题意；
B、2+4＜7，故不能构成三角形，故此选项不符合题意；
C、3+4＜8，故不能构成三角形，故此选项不符合题意；
D、2+3＞4，故能构成三角形，故此选项符合题意．
故选：D．
【点评】本题考查了三角形的三边的关系，正确理解三边关系定理是解题关键．
3．（3分）下列多边形中，内角和与外角和相等的是（ ）
A．B．
C．D．
【分析】根据多边形的内角和公式（n﹣2）•180°与多边形的外角和定理列式进行计算即可得解．
【解答】解：设所求多边形的边数为n，根据题意得：
（n﹣2）•180°＝360°，
解得n＝4．
故选：B．
【点评】本题考查了多边形的内角和公式与外角和定理，熟记公式与定理是解题的关键．
4．（3分）下列计算中正确的是（ ）
A．（x2）2＝x5B．x3﹣x2＝x
C．（a﹣b）2＝a2﹣b2D．﹣x2•x＝﹣x3
【分析】根据幂的乘方计算，完全平方公式，同底数幂乘法计算和合并同类项，逐项分析判断即可．
【解答】解：A、（x2）2＝x4，原式计算错误，不符合题意；
B、x3与x2不是同类项，不能合并，原式计算错误，不符合题意；
C、（a﹣b）2＝a2﹣2ab+b2，原式计算错误，不符合题意；
D、﹣x2•x＝﹣x3，原式计算正确，符合题意；
故选：D．
【点评】本题主要考查了幂的乘方计算，完全平方公式，同底数幂乘法计算和合并同类项，熟知相关计算法则是解题的关键．
5．（3分）2022年2月8日上午，谷爱凌在女子滑雪大跳台决赛中，获得了北京冬奥会雪上项目的首金．如图所示，大跳台的∠B＝35°，∠C＝y°，∠BAD＝x°，请找出y与x的关系式（ ）
A．y＝145﹣xB．y＝x﹣35C．y＝x+55D．y＝x+35
【分析】直接利用三角形的外角性质求解即可．
【解答】解：∵∠BAD是△ABC的外角，∠B＝35°，∠C＝y°，∠BAD＝x°，
∴∠BAD＝∠B+∠C，
即x＝35+y，
∴y＝x﹣35．
故选：B．
【点评】本题主要考查三角形的外角性质，解答的关键是明确三角形的外角性质：三角形的外角等于与其不相邻的两个内角之和．
6．（3分）如图，AC＝BC，下列条件不能判定△ACD与△BCD全等的是（ ）
A．AD＝BDB．∠ACD＝∠BCD
C．∠ADC＝∠BDCD．点O是AB的中点
【分析】根据全等三角形的判定方法可对A、B、C选项进行判断；根据等腰三角形的性质和全等三角形的判定方法可对D选项进行判断．
【解答】解：∵AC＝BC，CD＝CD，
∴当AD＝BD时，△ACD≌△BCD（SSS）；
当∠ACD＝∠BCD时，△ACD≌△BCD（SAS）；
当∠ADC＝∠BDC时，不能判断△ACD≌△BCD；
当O点为AB的中点时，CO平分∠ACB，∠ACD＝∠BCD，△ACD≌△BCD（SAS）．
故选：C．
【点评】本题考查了全等三角形的判定：熟练掌握全等三角形的5种判定方法是解决问题的关键．选用哪一种方法，取决于题目中的已知条件．
7．（3分）如图，OC平分∠AOB，在OC上取一点P，作PF⊥OB，已知OF＝5cm，△POF的面积为5cm2，点E是射线OA上一动点．则PE长度的最小值为（ ）
A．1cmB．1.5cmC．2cmD．2.5cm
【分析】先求解PF＝2，过P点作PH⊥OB于H，根据角平分线的性质得到PH＝PF＝2cm，然后根据垂线段最短求解．
【解答】解：∵OF＝5cm，△FOP的面积为5cm2，PF⊥OB，
∴，
∴PF＝2，
过P点作PH⊥OA于H，如图：
∵OC平分∠AOB，PH⊥OA，PF⊥OB，
∴PF＝PH＝2cm，
∵点E是射线OA上的动点，
∴PE的最小值为2cm，
故选：C．
【点评】本题考查了角平分线的性质，掌握角平分线的性质是解题的关键．
8．（3分）已知a+＝4，则a2+＝（ ）
A．12B．14C．16D．18
【分析】先把已知方程两边平方，再变形得结论．
【解答】解：∵a+＝4，
∴（a+）2＝42．
即a2+2+＝16．
∴a2+＝14．
故选：B．
【点评】本题考查分式的化简求值，掌握完全平方公式是解决本题的关键．
9．（3分）如图，BD是△ABC的角平分线，AE⊥BD，垂足为F．若∠ABC＝35°，∠C＝50°，则∠CDE的度数为（ ）
A．35°B．40°C．45°D．50°
【分析】根据角平分线的定义和垂直的定义得到∠ABD＝∠EBD＝∠ABC＝，∠AFB＝∠EFB＝90°，推出AB＝BE，根据等腰三角形的性质得到AF＝EF，求得AD＝ED，得到∠DAF＝∠DEF，根据三角形的外角的性质即可得到结论．
【解答】解：∵∠ABC＝35°，∠C＝50°，
∴∠BAC＝180°﹣35°﹣50°＝95°，
∵BD是△ABC的角平分线，
∴∠ABF＝∠EBF，
∵AE⊥BD，
∴∠AFB＝∠EFB＝90°，
在△ABF和△EBF中，
，
∴△ABF≌△EBF（ASA），
∴AB＝EB，AF＝EF，
∴∠BAE＝∠BEA，DA＝DE，
∴∠DAE＝∠DEA，
∴∠BAE+∠DAE＝∠BEA+∠DEA，
∴∠DEB＝∠DAB＝95°，
∴∠CDE＝∠DEB﹣∠C＝45°，
故选：C．
【点评】本题考查了三角形的内角和，全等三角形的判定和性质，三角形的外角的性质，熟练掌握全等三角形的判定和性质是解题的关键．
10．（3分）如图，在Rt△ABC中，AB＝CB，BO⊥AC，把△ABC折叠，使AB落在AC上，点B与AC上的点E重合，展开后，折痕AD交BO于点F，连接DE，EF．
下列结论：①AB＝2BD；②图中有4对全等三角形；③BD＝BF；④若将△DEF沿EF折叠，则点D不一定落在AC上；⑤S四边形DFOE＝S△AOF，上述结论中正确的个数是（ ）
A．1B．2C．3D．4
【分析】由等腰直角三角形的性质可得AO＝CO＝BO，∠ABO＝∠BAO＝∠C＝∠CBO＝45°，由折叠的性质可得∠ABD＝∠AED＝90°，BD＝DE，AB＝AE，利用全等三角形的性质依次判断可求解．
【解答】解：∵AB＝CB，BO⊥AC，∠ABC＝90°，
∴AO＝CO＝BO，∠ABO＝∠BAO＝∠C＝∠CBO＝45°，
∵把△ABC折叠，使AB落在AC上，点B与AC上的点E重合，
∴△ABD≌△AED，
∴∠ABD＝∠AED＝90°，BD＝DE，AB＝AE，
∴∠EDC＝∠C＝45°，
∴DE＝EC，
∴CD＝DE＝BD，
∴AB＝BC＝BD+CD＝（1+）BD，故①错误，
在△ABO和△CBO中，
，
∴△ABO≌△CBO（SAS），
∵△ABD≌△AED，
∴∠BAD＝∠EAD，∠ADB＝∠ADE，
在△ABF和△AEF中，
，
∴△ABF≌△AEF（SAS），
在△BDF和△EDF中，
，
∴△BDF≌△EDF（SSS），
∴图中共有4对全等三角形，故②正确；
∵∠AFO＝90°﹣∠FAO，∠ADB＝90°﹣∠BAD，
∴∠ADB＝∠AFO＝∠BFD，
∴BF＝BD，故③正确；
∵△BDF≌△EDF，
∴∠FBD＝∠FED＝45°，
∵∠AED＝90°，
∴∠AEF＝∠DEF，
∴将△DEF沿EF折叠，则点D一定落在AC上，故④错误；
连接CF，
∵AO＝CO，
∴S△AFO＝S△CFO，
∵∠AEF＝∠ACB＝45°，
∴EF∥BC，
∴S△EFD＝S△EFC，
∴S四边形OEDF＝S△CFO，
∴S四边形OEDF＝S△AFO，故⑤正确，
故选：C．
【点评】本题考查了翻折变换，全等三角形的判定和性质，等腰直角三角形的性质，灵活运用全等三角形的判定是本题的关键．
二、填空题
11．（3分）计算：2m2•（3m）2＝ 18m4 ．
【分析】先利用积的乘方法则计算乘方，再根据单项式乘单项式和同底数幂相乘法则计算乘法即可．
【解答】解：原式＝2m2•9m2
＝18m4，
故答案为：18m4．
【点评】本题主要考查了单项式乘单项式、同底数幂相乘和积的乘方，解题关键是熟练掌握单项式乘单项式法则、同底数幂相乘法则和积的乘方法则．
12．（3分）若992﹣1＝ 9800 ．
【分析】直接利用平方差公式分解因式即可求出答案．
【解答】解：992﹣1
＝（99+1）×（99﹣1）
＝100×98
＝9800．
故答案为：9800．
【点评】此题主要考查了平方差公式，熟练掌握平方差公式是解题的关键．
13．（3分）若多项式x2+（m﹣1）x+9是一个完全平方式，则m的值是 ﹣5或7 ．
【分析】根据完全平方式的特点得出（m﹣1）x＝±2•x•3，再求出即可．
【解答】解：∵x2+（m﹣1）x+9是一个完全平方式，
∴（m﹣1）x＝±2•x•3，
∴m﹣1＝±6，
∴m＝﹣5或7，
故答案为：﹣5或7．
【点评】本题考查了完全平方式，能熟记完全平方式的特点是解此题的关键，注意：完全平方式有a2+2ab+b2和a2﹣2ab+b2两个．
14．（3分）如图，AD⊥BC于点D，D为BC的中点，连接AB，∠ABC的平分线交AD于点O，连接OC，若∠AOC＝120°，则∠ABC＝ 60° ．
【分析】先由三角形的外角性质得∠C＝30°，因为AD⊥BC，D为BC的中点，所以OD是BC的垂直平分线，则∠OBC＝∠C＝30°，因为BO是∠ABC的角平分线，则BO是∠ABC的角平分线，即可作答．
【解答】解：∠AOC＝120°，AD⊥BC，
∴∠ODC＝90°，∠C＝120°﹣90°＝30°，
∵AD⊥BC，D为BC的中点，
∴OD是BC的垂直平分线，
∴OB＝OC，
∴∠OBC＝∠C＝30°，
∵BO是∠ABC的角平分线，
∴∠ABC＝2∠OBC＝60°，
故答案为：60°．
【点评】本题考查了三角形的外角性质以及垂直平分线的判定与性质，等边对等角，以及角平分线的定义，学会判断各角之间的关系是解题的关键．
15．（3分）如图，在RT△ABC中，∠ACB＝90°，AC＝BC，直角顶点C在y轴上，点A在x轴上，OC＝2OA＝4，则点B的坐标为 （4，2） ．
【分析】作BH⊥y轴于H，易得OA＝2根据等腰直角三角形的性质结合AAS证明△ACO≌△CBH（AAS），得到CO＝BH＝4，OA＝CH＝2，即可得出点B坐标．
【解答】解：作BH⊥y轴于H，如图，
∴∠BHC＝∠COA＝90°，
∴∠CBH+∠BCH＝90°，
∵OC＝2OA＝4，
∴OA＝2，
∵△ABC是等腰直角三角形，
∴CA＝BC，∠ACB＝90°，
∴∠ACO+∠BCH＝90°，
∴∠ACO＝∠CBH，
在△ACO和△BCH中，
，
∴△ACO≌△CBH（AAS），
∴CO＝BH＝4，OA＝CH＝2，
∴OH＝4﹣2＝2，
∴B（4，2），
故答案为：（4，2）．
【点评】本题考查等腰直角三角形的性质，全等三角形的判定与性质，点的坐标，熟练掌握全等三角形的判定与性质是解题的关键．
16．（3分）若关于x的不等式组，有且只有3个整数解，且关于y的一元一次方程2y+6＝3a的解是正整数，则所有满足条件的整数a的值之和为 18 ．
【分析】根据关于x的不等式组，有且只有3个整数解，可以求得a的取值范围，再根据关于y的一元一次方程2y+6＝3a的解是正整数，可以得到a的值，然后即可求得所有满足条件的整数a的值之和．
【解答】解：，
解不等式①，得：x≤3，
解不等式②，得：x＞，
∵关于x的不等式组，有且只有3个整数解，
∴该不等式组的三个整数解为3，2，1，
∴0≤＜1，
解得7.5≤a＜11，
由2y+6＝3a可得y＝，
∵关于y的一元一次方程2y+6＝3a的解是正整数，
∴a＝8或10，
∴所有满足条件的整数a的值之和为8+10＝18，
故答案为：18．
【点评】本题考查解一元一次不等式组、解一元一次方程，解答本题的关键是明确题意，求出a的值．
17．（3分）下列说法：
①已知a，b，c满足a2+6a+b2﹣4b+c2﹣2c+14＝0，则a+b+c＝0；
②已知a，b，c是正整数，a＞b，且a2﹣（b﹣c）2＝5，则a＝3，b＝2，c＝4；
③若实数x，y，m满足2x+y+m＝5，3x+2y+m＝8，则代数式3xy﹣1的值可以是6．
其中正确的是 ① （请在横线上填写序号）．
【分析】①先把等式的左边进行配方，再根据非负数的性质求解；
②先把等式的左边分解因式，再根据“a，b，c是正整数，a＞b”进行求解；
③先假设结论成立，再根据反证法求解．
【解答】解：①∵a2+6a+b2﹣4b+c2﹣2c+14＝（a+3）2+（b﹣2）2+（c﹣1）2＝0，
∴a＝﹣3，b＝2，c＝1，
∴a+b+c＝﹣3+2+1＝0；
故①是正确的；
②∵a2﹣（b﹣c）2＝（a+b﹣c）（a﹣b+c）＝5，
∵a，b，c是正整数，
∴a＝3，b﹣c＝±2，
∵a＞b，
∴b＝1或b＝2，
∴c＝3或c＝4，
∴a＝3，b＝1，c＝3或a＝3，b＝2，c＝4，
故②是错误的；
③由题意得：x+y＝3，
若3xy﹣1的值可以是6，
则：xy＝，
则：x、y为方程z2﹣3z+＝0的解，
∵Δ＝9﹣4×＜0，
∴不存在实数x、y，
故③是错误的；
故答案为：①．
【点评】本题考查了配方法的应用，掌握因素分解是解题的关键．
三、解答题：
18．计算：
（1）5x（x+2y﹣8）；
（2）（3x+2y）（﹣2y+3x）．
【分析】（1）根据单项式乘多项式法则计算即可；
（2）根据平方差公式计算即可．
【解答】解：（1）5x（x+2y﹣8）＝5x2+10xy﹣40x；
（2）（3x+2y）（﹣2y+3x）
＝（3x+2y）（3x﹣2y）
＝9x2﹣4y2．
【点评】本题考查了平方差公式，单项式乘多项式，熟练掌握运算法则是解题的关键．
19．因式分解：
（1）24a3bc2﹣8ab2；
（2）（m+3n）（4m﹣n）﹣（m+3n）（m﹣7n）．
【分析】（1）依据题意，运用提公因式法即可分解因式得解；
（2）依据题意，根据提公因式法进行分解可以得解．
【解答】解：（1）24a3bc2﹣8ab2
＝8ab（3a2c2﹣b）．
（2）（m+3n）（4m﹣n）﹣（m+3n）（m﹣7n）
＝（m+3n）（4m﹣n﹣m+7n）
＝（m+3n）（3m+6n）
＝3（m+3n）（m+2n）．
【点评】本题主要考查了提公因式法的运用，解题时要熟练掌握并灵活运用提公因式法分解因式是关键．
20．如图，点D在线段BC上，AB∥CE，AB＝CD，BD＝CE．
（1）求作∠ADE的平分线，并交AE于点F（要求：尺规作图，保留作图痕迹，不写作法）；
（2）在（1）问的条件下试证明：AF＝EF，请将以下推导过程补充完整．
证明：∵AB∥CE，
∴∠B＝∠C．
在△ABD和△DCE中
，
∴△ABD≌△DCE（ SAS ），
∴ AD＝DE ．
∵DF平分∠ADE，
∴∠ADF＝∠EDF．
在△ADF和△EDF中
，
∴△ADF≌△EDF（SAS），
∴AF＝EF．
【分析】（1）按照角平分线的作图方法作图即可．
（2）根据全等三角形的判定与性质可得答案．
【解答】（1）解：如图，DF即为所求.
（2）证明：∵AB∥CE，
∴∠B＝∠C．
在△ABD和△DCE中，
，
∴△ABD≌△DCE（SAS），
∴AD＝DE．
∵DF平分∠ADE，
∴∠ADF＝∠EDF．
在△ADF和△EDF中，
，
∴△ADF≌△EDF（SAS），
∴AF＝EF．
故答案为：BD＝CE；SAS；AD＝DE；∠ADF＝∠EDF．
【点评】本题考查作图﹣基本作图、全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解答本题的关键．
21．先化简，再求值：[（a﹣b）2﹣2b（a﹣b）﹣（a+b）（a﹣b）]÷（﹣4b），其中a＝1，b＝．
【分析】根据整式的加减运算法则以及整式的乘除法则进行化简，然后将a与b代入原式即可求出答案．
【解答】解：原式＝（a2﹣2ab+b2﹣2ab+2b2﹣a2+b2）÷（﹣4b）
＝（4b2﹣4ab）÷（﹣4b）
＝﹣b+a，
当a＝1，b＝﹣时，
原式＝1+＝．
【点评】本题考查整式的运算，解题的关键是熟练运用整式的加减运算法则以及整式的乘除法则，本题属于基础题型．
22．为深入学习贯彻党的二十大精神，引领广大职工准确把握党的二十大报告的丰富内涵、精神实质、实践要求，江北区教育工会开展了学习二十大知识竞赛活动，根据竞赛活动的成绩划分了四个等级：A：合格，B：良好，C：优秀，D：非常优秀．现随机抽查部分竞赛成绩的数据进行了整理、绘制成部分统计图：
请根据图中信息，解答下列问题：
（1）填空：a＝ 15% ，“优秀”对应扇形的圆心角度数为 90° ；
（2）请你补全条形统计图；
（3）若我区有8000名教职工，请你估计其中“优秀”和“非常优秀”的教职工共有多少人？
【分析】（1）根据“良好”的人数除以占比得出总人数，用“合 格”的人数除以总人数得出a，根据“优秀”的占比乘以 360° 得出“优秀”对应扇形的圆心角度数；
（2）根据“优秀”的占比乘以总人数得出“优秀”的人 数，进而补全统计图；
（3）用8000乘以“优秀”和“非常优秀”的占比即可求解．
【解答】解：（1）总人数为：60÷20%＝300 人，
∴a＝45÷300＝15%，
“优秀”对应扇形的圆心角度数为 360°×25%＝90°；
故答案为：15%，90°；
（2）“优秀”的人数：300×25%＝75人，补全统计图如图所示：
（3）其中“优秀”和“非常优秀”的教职工共有：8000×（1﹣20%﹣15%）＝5200（人），
答：其中“优秀”和“非常优秀”的教职工共5200人．
【点评】本题主要考查了条形统计图和扇形统计图的综合运 用，样本估计总体，读懂统计图，从不同的统计图 中得到必要的信息是解决问题的关键，条形统计图 能清楚地表示出每个项目的数据；扇形统计图直接 反映部分占总体的百分比大小．
23．如图，点E在CD上，BC与AE交于点F，AB＝CB，BE＝BD，∠1＝∠2．
（1）求证：△ABE≌△CBD；
（2）若∠2＝55°，求∠3的度数．
【分析】（1）根据等式的性质得∠ABE＝∠CBD，再利用SAS即可证明结论成立；
（2）由△ABE≌△CBD可得∠AEB＝∠D，由∠2＝55°可求得∠BED+∠D＝125°，根据平角定义即可求得．
【解答】（1）证明：（1）∵∠1＝∠2．
∴∠ABE＝∠CBD，
在△ABE和△CBD中，
，
∴△ABE≌△CBD（SAS）；
（2）解：∵△ABE≌△CBD，
∴∠AEB＝∠D，
∵∠2＝55°，
∴∠BED+∠D＝125°，
∴∠BED+∠AEB＝125°，
∴∠3＝55°．
【点评】本题主要考查了全等三角形的判定与性质，三角形的内角和定理等知识，熟练掌握全等三角形的判定与性质是解题的关键．
24．为改善校园环境，提升办学品质，重庆市鲁能巴蜀中学计划拆除网球场，新建综合大楼．已知2辆甲型除渣车和3辆乙型除渣车每天可以除渣170吨，3辆甲型除渣车和2辆乙型除渣车每天可以除渣180吨．
（1）求甲、乙两种型号的除渣车每辆每天分别可以除渣多少吨？
（2）施工期间，学校决定租赁甲、乙两种型号的除渣车共20辆，已知每辆甲型除渣车租赁价格为15万元，每辆乙型除渣车租赁价格为12万元，要想使租赁除渣车的总费用不超过261万元，且每天除渣总量又不低于650吨，请你求出所有的租赁方案．
【分析】（1）设甲型除渣车每辆每天可以除渣x吨，乙型除渣车每辆每天可以除渣y吨，根据“2辆甲型除渣车和3辆乙型除渣车每天可以除渣170吨，3辆甲型除渣车和2辆乙型除渣车每天可以除渣180吨”，可列出关于x，y的二元一次方程组，解之即可得出结论；
（2）设租赁m辆甲型除渣车，则租赁（20﹣m）辆乙型除渣车，根据“租赁除渣车的总费用不超过261万元，且每天除渣总量又不低于650吨”，可列出关于m的一元一次不等式组，解之可得出m的取值范围，再结合m为正整数，即可得出各租赁方案．
【解答】解：（1）设甲型除渣车每辆每天可以除渣x吨，乙型除渣车每辆每天可以除渣y吨，
根据题意得：，
解得：．
答：甲型除渣车每辆每天可以除渣40吨，乙型除渣车每辆每天可以除渣30吨；
（2）设租赁m辆甲型除渣车，则租赁（20﹣m）辆乙型除渣车，
根据题意得：，
解得：5≤m≤7，
又∵m为正整数，
∴m可以为5，6，7，
∴学校共有3种租赁方案，
方案1：租赁5辆甲型除渣车，15辆乙型除渣车；
方案2：租赁6辆甲型除渣车，14辆乙型除渣车；
方案3：租赁7辆甲型除渣车，13辆乙型除渣车．
【点评】本题考查了二元一次方程组的应用以及一元一次不等式组的应用，解题的关键是：（1）找准等量关系，正确列出二元一次方程组；（2）根据各数量之间的关系，正确列出一元一次不等式组．
25．数学活动课中，老师给出以下问题：
（1）如图1，在△ABC中，D是边BC的中点，若AB＝5，AC＝9，则中线AD长度的取值范围 2＜AD＜7 ．
（2）如图2，在△ABC中，D是边BC的中点，过D点的射线DE交边AB于E，再作DF⊥DE交边AC于点F，连接EF，请探索由三条线段BE、EF、CF构成的三角形的形状，并说明理由．
（3）已知：如图3，AB＝AC，∠BAC＝∠CDE＝90°，且DC＝DE，F是线段BE的中点．求证：AF⊥FD．
【分析】（1）延长AD到E，使DE＝AD，连接CE，证明△ADB≌EDC，根据全等三角形的性质得到CE＝AB，根据三角形的三边关系解答即可；
（2）延长ED到点G，使DG＝ED，连接GF，GC，证明△DBE≌△DCG，根据全等三角形的性质得到BE＝CG，∠B＝∠GCD，根据三角形内角和定理得到∠ACB+∠ABC＝180°﹣∠A，分∠A为锐角、∠A为直角三种情况解答；
（3）延长DF至G，使FG＝DF，连接EG、AG，证明△ACD≌△ABG，得到AG＝AD，根据等腰三角形的三线合一证明结论．
【解答】解：（1）如图1，延长AD到E，使DE＝AD，连接CE，
在△ADB和△EDC中，
，
∴△ADB≌EDC（SAS），
∴CE＝AB，
在△ACE中，AC﹣CE＜AE＜AC+CE，
∴AC﹣AB＜2AD＜AC+AB，
∵AB＝5，AC＝9，
∴4＜2AD＜14，
∴2＜AD＜7，
故答案为：2＜AD＜7；
（2）如图2，线段BE、EF、CF构成的三角形是锐角三角形或钝角三角形或直角三角形，
理由如下：延长ED到点G，使DG＝ED，连接GF，GC，
∵ED⊥DF，
∴EF＝GF，
∵D是BC的中点，
∴BD＝CD，
在△BDE和△CDG中，
，
∴△DBE≌△DCG（SAS），
∴BE＝CG，∠B＝∠GCD，
∵∠ACB+∠ABC＝180°﹣∠A，
∴∠ACG＝∠GCD+∠ACB＝∠ABC+∠ACB＝180°﹣∠A°，
当∠A为锐角时，△FCG为钝角三角形，即由三条线段BE、EF、CF构成的三角形为钝角三角形，
当∠A为钝角时，△FCG为锐角三角形，即由三条线段BE、EF、CF构成的三角形为锐角三角形，
当∠A为直角时，△FCG为直角三角形，即由三条线段BE、EF、CF构成的三角形为直角三角形；
（3）如图3，延长DF至G，使FG＝DF，连接EG、AG，
∵F是BE的中点，
∴BF＝EF，
在△DFE与△GFB中，
，
∴△DFE≌△GFB（SAS），
∴BG＝DE，∠FBG＝∠FED，
∵∠BAC＝∠CDE＝90°，
∴∠B+∠DEF+∠CAD+∠CDA＝180°，
∵∠CAD+∠C+∠CDA＝180°，
∴∠C＝∠ABE+∠FED＝∠ABE+∠FBG＝∠ABG，
在△ACD与△ABG中，
，
∴△ACD≌△ABG（SAS），
∴AG＝AD，
∵DF＝FG，
∴AF⊥FD．
【点评】本题考查的是全等三角形的判定和性质、等腰直角三角形的判定和性质、四边形的内角和、三角形的内角和，掌握全等三角形的判定定理和性质定理、正确作出辅助线是解题的关键
26．现有长与宽分别为a、b的小长方形若干个，用两个这样的小长方形拼成如图1的图形，用四个相同的小长方形拼成图2的图形，请认真观察图形，解答下列问题：
（1）根据图中条件，请写出图1和图2所验证的关于a、b的关系式：（用含a、b的代数式表示出来）；
图1表示： （a+b）2＝a2+b2+2ab ；
图2表示： （a+b）2＝（a﹣b）2+4ab ；
根据上面的解题思路与方法，解决下列问题：
（2）若x+y＝8，x2+y2＝40，求xy的值；
（3）请直接写出下列问题答案：
①若2m+3n＝5，mn＝1，则2m﹣3n＝ ±1 ；
②若（4﹣m）（5﹣m）＝6，则（4﹣m）2+（5﹣m）2＝ 13 ．
（4）如图3，点C是线段AB上的一点，以AC，BC为边向两边作正方形，设AB＝7，两正方形的面积和S1+S2＝16，求图中阴影部分面积．
【分析】（1）图1中由两个长与宽分别为a、b的小长方形与一大一小两个正方形构成一个大的正方形，利用边长为（a+b）正方形的面积等于两个长方形的面积加边长分别为a，b的正方形的面积可得；图2中利用大正方形的面积等于4个长方形的面积加小正方形的面积可得；
（2）将xy根据完全平方公式用含有x+y，x2+y2的式子表示出来，然后代入求值即可．
（3）①利用（2m﹣3n）2＝（2m+3n）2﹣24mn，代入求值即可，②利用[（4﹣m）﹣（5﹣m）]2＝（4﹣m）2+（5﹣m）2﹣2（4﹣m）（5﹣m）代入求值即可；
（4）AB＝AC+BC，S1＝AC2，S2＝BC2，S阴影＝BC•CD＝BC•AC，可以利用（AC+BC）2＝AC2+BC2+2AC•BC代入求值即可．
【解答】解：（1）图1中，由图可知S大正方形＝（a+b）2，
S组成大正方形的四部分的面积之和＝a2+b2+2ab，
由题意得，S大正方形＝S组成大正方形的四部分的面积之和，
即（a+b）2＝a2+b2+2ab，
故答案为：（a+b）2＝a2+b2+2ab．
图2中，由图可知S大正方形＝（a+b）2，S小正方形＝（a﹣b）2，S四个长方形＝4ab，
由题图可知，S大正方形＝S小正方形+S四个长方形，
即（a+b）2＝（a﹣b）2+4ab，
故答案为：（a+b）2＝（a﹣b）2+4ab．
（2）∵（x+y）2＝x2+y2+2xy，
∴xy＝[（x+y）2﹣（x2+y2）]
∵x+y＝8，x2+y2＝40，
∴xy＝（64﹣40）
＝12．
（3）①由图2可得（2m﹣3n）2＝（2m+3n）2﹣24mn，
∵2m+3n＝5，mn＝1，
∴（2m﹣3n）2＝52﹣24＝1，
∴2m﹣3n＝±1．
故答案为：±1．
②由图1可得[（4﹣m）﹣（5﹣m）]2＝（4﹣m）2+（5﹣m）2﹣2（4﹣m）（5﹣m），
∴（4﹣m）2+（5﹣m）2＝[（4﹣m）﹣（5﹣m）]2+2（4﹣m）（5﹣m），
∵（4﹣m）（5﹣m）＝6，
∴原式＝1+2×6＝13．
故答案为：13．
（4）由题意得AB＝AC+CB，
∵AB＝7，
∴AC+CB＝7，
∵S1+S2＝16，
∴AC2+CB2＝16，
∵（AC+BC）2＝AC2+CB2+2AC•CB，
∴AC•CB＝[（AC+CB）2﹣（AC2+CB2）]
＝（49﹣16）
＝，
∴S阴影＝CD•CB＝AC•CB＝．
即图中阴影部分的面积为．
【点评】本题考查了完全平方公式的几何背景及完全平方公式的应用，解题的关键熟练掌握完全平方公式，并进行灵活运用．
题号
1
2
3
4
5
6
7
8
9
10
答案
D
D
B
D
B
C
C
B
C
C