

2024--2025学年人教版九年级数学上册期末真题重组卷 (原卷版)-A4
展开
这是一份2024--2025学年人教版九年级数学上册期末真题重组卷 (原卷版)-A4,共7页。试卷主要包含了 下列事件是必然事件的是等内容,欢迎下载使用。
(2023秋•上城区期末)
1. 下列事件是必然事件的是( )
A. 圆内接四边形对角和是
B. 九年级开展篮球赛,901班获得冠军
C. 抛掷一枚硬币,正面朝上
D. 打开电视,正好播放神舟十七号载人飞船发射实况
(2023秋•宁波期末)
2. 已知⊙O的半径为5,点P在⊙O外,则OP的长可能是( )
A. 3B. 4C. 5D. 6
(2023秋•江岸区期末)
3. 将一元二次方程配方后所得的方程是( )
A. B.
C. D.
(2023秋•上城区期末)
4. 某商场进行抽奖活动,每名顾客购物满元可以获得一次抽奖机会.抽奖箱中只有两种卡片:“中奖”和“谢谢惠顾”(两种卡片形状大小相同、质地均匀).下表是活动进行中的一组统计数据:
根据频率的稳定性,估计抽奖一次就中奖的概率约是( )
A. B. C. D.
(2023秋•澧县期末)
5. 在平面直角坐标系中,将抛物线先向右平移2个单位,再向上平移2个单位,得到的抛物线的解析式是( )
A. B. C. D.
(2023秋•上城区期末)
6. 如图,内接于,CD是的直径,连接BD,,则的度数是( )
A. B. C. D.
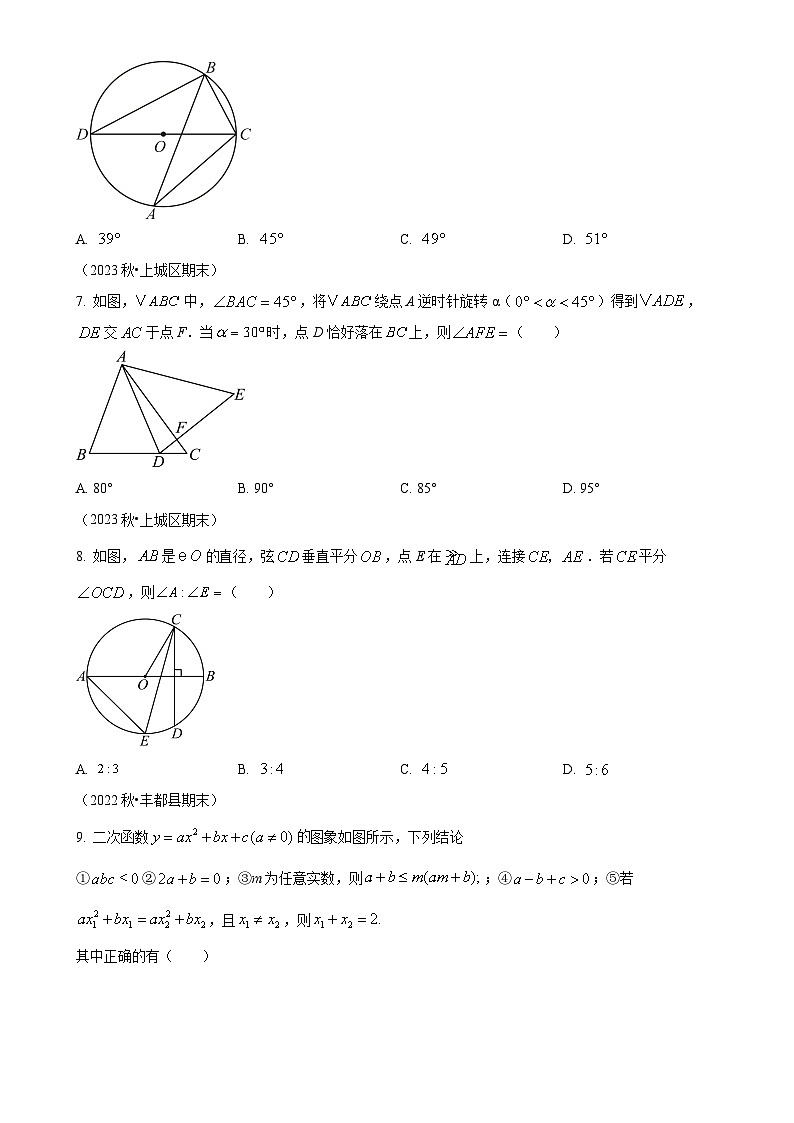
(2023秋•上城区期末)
7. 如图,中,,将绕点A逆时针旋转α()得到,交于点F.当时,点D恰好落在上,则( )
A. 80°B. 90°C. 85°D. 95°
(2023秋•上城区期末)
8. 如图,是直径,弦垂直平分,点E在上,连接.若平分,则( )
A. B. C. D.
(2022秋•丰都县期末)
9. 二次函数图象如图所示,下列结论
①②;③m为任意实数,则;④;⑤若,且,则
其中正确的有( )
A. 1个B. 2个C. 3个D. 4个
二.填空题(共8小题)
(2023秋•龙马潭区期末)
10. 若点与点B关于原点对称,则点B的坐标为______________.
(2023秋•上城区期末)
11. 有10张卡片,每张卡片上分别写有不同的自然数.任意抽取一张卡片,卡片上的数是的倍数的概率是______.
(2023秋•盘山县期末)
12. 若关于x一元二次方程没有实数根,则k的取值范围是______.
(2023秋•上城区期末)
13. 已知二次函数,则此函数的顶点坐标是______;若,当时,函数有最小值,则______.
(2019秋•汶上县期末)
14. 如图,是的直径,弦交于点P,,则的长为___.
(2024•海淀区)
15. “青山绿水,畅享生活”,人们经常将圆柱形竹筒改造成生活用具,图1所示是一个竹筒水容器,图为该竹筒水容器的截面.已知截面的半径为,开口宽为,这个水容器所能装水的最大深度是________.
(2023秋•北流市期末)
16. 如图,在边长为2的正方形中,点E是线段上异于A,C的动点,将线段绕着点B顺时针旋转得到,连接,则的最大面积为________.
(2021秋•聊城期末)
17. 如图1是我国著名建筑“东方之门”,它通过简单的几何曲线处理,将传统文化与现代建筑融为一体,最大程度地传承了中国的历史文化.“门”的内侧曲线呈抛物线形,如图2,已知其底部宽度为80米,高度为200米,则离地面150米处的水平宽度(即的长)为_____米.
三.解答题(共9小题)
(2022秋•环江县期末)
18. 解方程:.
(2023秋•齐河县期末)
19. 2023年9月23日,第19届亚运会在杭州开幕,电子竞技首次成为亚运会正式比赛项目.张琪和李荷是电竞游戏的爱好者,她们相约一起去现场为中国队加油,现场的观赛区分为、、、四个区域,购票以后系统随机分配观赛区域.
(1)张琪购买门票在区观赛的概率为___________;
(2)求张琪和李荷在同一区域观看比赛概率.(请用画树状图或列表等方法说明理由)
(2024•海淀区)
20. 如图,在中,,将绕点A逆时针旋转得到,使点在的延长线上.求证:.
(2023秋•江都区期末)
21. 已知关于的一元二次方程.
(1)求证:方程有两个实数根;
(2)若方程的两个根都是负根,求k的取值范围.
(2023秋•东城区期末)
22. 在平面直角坐标系中,点在抛物线上,设该抛物线的对称轴为直线.
(1)求t的值;
(2)已知,是该抛物线上的任意两点,对于,,都有,求m的取值范围.
(2023秋•荔城区校级期末)
23. 如图,为的直径,点C在外,的平分线与交于点D,.
(1)与有怎样的位置关系?请说明理由;
(2)若,求的长.
(2023秋•岳阳县期末)
24. 公安交警部门提醒市民,骑车出行必须严格遵守“一盔一带”的规定.某头盔经销商统计了某品牌头盔4月份到6月份的销量,该品牌头盔4月份销售150个,6月份销售216个,且从4月份到6月份销售量的月增长率相同.
(1)为求该品牌头盔销售量的月增长率,设增长率为a,依题意列方程为____________;
(2)若此种头盔的进价为30元个,测算在市场中,当售价为40元个时,月销售量为600个,若在此基础上售价每涨价1元个,则月销售量将减少10个,若该品牌头盔涨价x元个,销售总利润为y,列出y与x的函数关系式.
①当x为多少时?销售总利润达到10000元.
②当x为多少时?销售总利润达到最大,求最大总利润.
(2023秋•楚雄市校级期末)
25. 如图,为的直径,为上一点,为的中点,点在的延长线上,且.
(1)求证:为的切线;
(2)若,求图中阴影部分面积.
(2023秋•石景山区期末)
26. 投掷实心球是北京市初中学业水平考试体育现场考试的选考项目之一.实心球被投掷后的运动路线可以看作是抛物线的一部分.建立如图所示的平面直角坐标系,实心球从出手(点处)到落地的过程中,其竖直高度(单位:)与水平距离(单位:)近似满足二次函数关系.
小石进行了三次训练,每次实心球的出手点的竖直高度为.记实心球运动路线的最高点为,训练成绩(实心球落地点的水平距离)为(单位:).训练情况如下:
根据以上信息,
(1)求第二次训练时满足的函数关系式;
(2)小石第二次训练的成绩为______;
(3)直接写出训练成绩,,的大小关系.
抽奖次数
1000
抽到“中奖”卡片的次数
中奖的频率
第一次训练
第二次训练
第三次训练
训练成绩
最高点
满足的函数关系式
相关试卷
这是一份2024-2025学年人教版数学九年级上册期末模拟练习 (真题重组卷)-,共25页。
这是一份沪科版九年级数学上册举一反三专题24.1期末真题重组卷(沪科版)特训(原卷版+解析),共33页。
这是一份苏科版九年级数学上册举一反三系列专题5.1期末真题重组卷特训(原卷版+解析),共29页。









