

期末真题重组卷(模拟练习)-2024-2025学年苏科版数学九年级上册
展开
这是一份期末真题重组卷(模拟练习)-2024-2025学年苏科版数学九年级上册,共19页。试卷主要包含了mm等内容,欢迎下载使用。
1.(2023秋•开福区校级期末)在一个不透明的口袋中装有3个白球,4个红球和5个黑球,它们除颜色外都相同,从中随机摸出一个球,恰好是白球的概率为( )
A.B.C.D.
2.(2024春•凉州区校级期末)小明在处理一组数据“12,12,28,35,■”时,不小心将其中一个数据污染了,只记得该数据在30~40之间,则“■”在范围内无论为何值都不影响这组数据的( )
A.平均数B.众数C.中位数D.方差
3.(2023秋•凉州区校级期末)用配方法解方程x2+8x+7=0,则配方正确的是( )
A.(x+4)2=9B.(x﹣4)2=9C.(x﹣8)2=16D.(x+8)2=57
4.(2023秋•宝丰县期末)对甲、乙、丙、丁四名射击选手进行射击测试,每人射击10次,平均成绩均为9.5环,方差如表所示:则四名选手中成绩最稳定的是( )
A.甲B.乙C.两D.丁
5.(2022秋•陈仓区期末)一元二次方程x2+2x﹣1=0的根的情况是( )
A.只有一个实数根
B.有两个相等的实数根
C.有两个不相等的实数根
D.没有实数根
6.(2022秋•延边州期末)2022年北京冬奥会女子冰壶比赛,有若干支队伍参加了单循环比赛(每两队之间都赛一场),单循环比赛共进行了45场,共有多少支队伍参加比赛?设共有x支队伍参加比赛,则所列方程为( )
A.x(x+1)=45B.=45
C.x(x﹣1)=45D.=45
7.(2021秋•南宁期末)如图,在⊙O中,∠ABC=60°,则∠AOC的大小是( )
A.30°B.120°C.135°D.150°
8.(2023秋•凉州区期末)工程上常用钢珠来测量零件上小孔的宽口,如果钢珠的直径为10mm,钢珠上顶端离零件上表面的距离为8mm,如图,则这个零件小孔的宽口AB等于( )mm.
A.4B.6C.7D.8
二.填空题(共8小题)
9.(2024春•雁塔区校级期末)如图是由7个相同的小正方形和4个相同的大正方形组成的图形,在这个图形内任取一点P,则点P落在阴影部分的概率为 .
10.(2024春•西丰县期末)小明参加“强国有我”主题演讲比赛,其演讲形象、内容、效果三项的成绩分别是70分、90分、80分.若将三项得分依次按2:4:4的比例确定最终成绩,则小明的最终比赛成绩为 分.
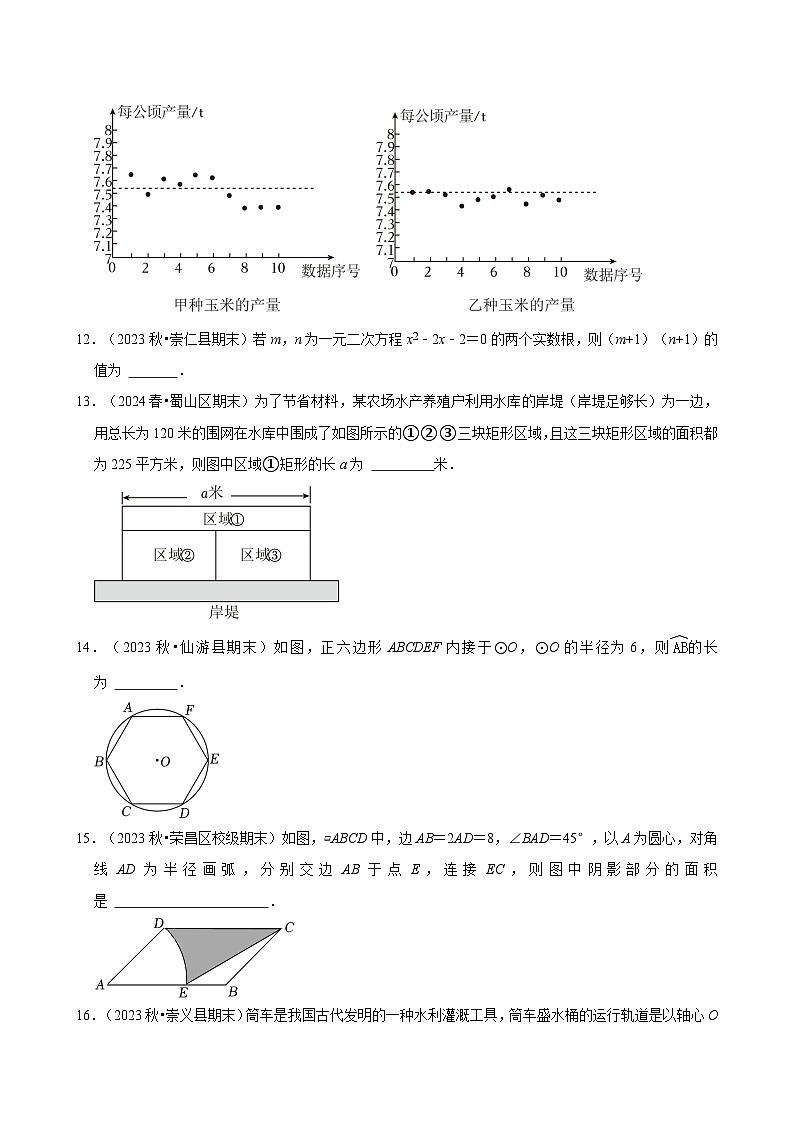
11.(2024春•交城县期末)农科院计划为某地选择合适的甜玉米种子.选择种子时,甜玉米的产量和产量的稳定性是农科院所关心的问题.为了解甲、乙两种玉米的相关情况,农科院各用10块自然条件相同的试验田进行试验,得到数据如图.则甲、乙两种甜玉米产量的方差大小关系为 .(填“<”或“>”)
12.(2023秋•崇仁县期末)若m,n为一元二次方程x2﹣2x﹣2=0的两个实数根,则(m+1)(n+1)的值为 .
13.(2024春•蜀山区期末)为了节省材料,某农场水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为120米的围网在水库中围成了如图所示的①②③三块矩形区域,且这三块矩形区域的面积都为225平方米,则图中区域①矩形的长a为 米.
14.(2023秋•仙游县期末)如图,正六边形ABCDEF内接于⊙O,⊙O的半径为6,则的长为 .
15.(2023秋•荣昌区校级期末)如图,▱ABCD中,边AB=2AD=8,∠BAD=45°,以A为圆心,对角线AD为半径画弧,分别交边AB于点E,连接EC,则图中阴影部分的面积是 .
16.(2023秋•崇义县期末)筒车是我国古代发明的一种水利灌溉工具,筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图1.唐代陈廷章在《水轮赋》中写道“水能利物,轮乃曲成”.如图2,已知圆心O在水面上方,且⊙O被水面截得弦AB长为8米,若点C为运行轨道的最低点,点C到弦AB所在直线的距离是2,则⊙O的半径长为 米.
三.解答题(共8小题)
17.(2023秋•兰州期末)解方程:x2﹣6x+5=0(两种方法).
18.(2024春•榆阳区期末)在一个不透明的袋子里,装有6个红球、3个黑球、1个白球,它们除颜色外都相同.
(1)求从袋中任意摸出一个球为红球的概率;
(2)现从袋中取走若干个红球,并放入相同数量的白球,充分摇匀后,要使从袋中随机摸出一个球是白球的概率是,问取走了多少个红球?
19.(2023秋•潼南区期末)已知关于x的一元二次方程mx2﹣2x﹣4=0有两个实数根.
(1)若方程的一个根是2,求m的值;
(2)求m的取值范围.
20.(2023秋•荣昌区校级期末)某商店销售一种成本为每千克40元的产品,根据市场分析,若按照每千克50元销售,一个月能售出这种产品500千克;销售单价每涨1元,月销售量就减少10千克.
(1)销售单价为58元时,这种产品的月销量是多少千克?
(2)该商店想在月销售成本不高于10000元的情况下,使得月销售利润达到8000元,销售单价应定为多少元?
21.(2023秋•东城区期末)如图,AB是⊙O的弦,半径OD⊥AB于点C.若AB=16,CD=2,求⊙O的半径的长.
22.(2023秋•盖州市期末)如图,已知△ABC,以AB为直径的⊙O分别交AC,BC于点D,E.连接DE,且ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=2.求CD的长.
23.(2023秋•曲周县期末)在⊙O中,弦CD与直径AB相交于点P,∠ABC=63°.
(1)如图①,若∠APC=100°,求∠ABD;
(2)如图②,若CD⊥AB,过点D作⊙O的切线,与AB的延长线相交于点E,求∠E的大小.
24.(2024春•红旗区校级期末)百度推出了“文心一言”AI聊天机器人(以下简称A款),抖音推出了“豆包”AI聊天机器人(以下简称B款).有关人员开展了A,B两款AI聊天机器人的使用满意度评分测验,并从中各随机抽取20份,对数据进行整理、描述和分析(评分分数用x表示,分为四个等级:不满意x<70,比较满意70≤x<80,满意80≤x<90,非常满意x≥90),下面给出了部分信息:
抽取的对A款AI聊天机器人的评分数据中“满意”的数据:
84,86,86,87,88,89;
抽取的对B款AI聊天机器人的评分数据:
66,68,69,81,84,85,86,87,87,87,88,89,95,97,98,98,98,98,99,100.
抽取的对A,B款AI聊天机器人的评分统计表
根据以上信息,解答下列问题:
(1)上述图表中a= ,b= ,c= ;
(2)根据以上数据,你认为哪款AI聊天机器人更受用户喜爱?请说明理由(写出一条理由即可);
(3)在此次测验中,有240人对A款AI聊天机器人进行评分、300人对B款AI聊天机器人进行评分,请通过计算,估计此次测验中对AI聊天机器人不满意的共有多少人?
期末真题重组卷(模拟练习)-2024-2025学年数学九年级上册苏科版
参考答案与试题解析
一.选择题(共8小题)
1.(2023秋•开福区校级期末)在一个不透明的口袋中装有3个白球,4个红球和5个黑球,它们除颜色外都相同,从中随机摸出一个球,恰好是白球的概率为( )
A.B.C.D.
【解答】解:∵在一个不透明的口袋中装有3个白球,4个红球和5个黑球,
∴从中随机摸出一个球,恰好是白球的概率==.
故选:A.
2.(2024春•凉州区校级期末)小明在处理一组数据“12,12,28,35,■”时,不小心将其中一个数据污染了,只记得该数据在30~40之间,则“■”在范围内无论为何值都不影响这组数据的( )
A.平均数B.众数C.中位数D.方差
【解答】解:一组数据“12,12,28,35,■”,该数据■在30~40之间,
四个数据的和随数据■的变化而变化,所以平均数是变化的,选项A错误.
众数也变化,选项B错误.
中位数是28,不变,选项C正确.
因为平均数改变,方差随着改变,选项D错误.
故选:C.
3.(2023秋•凉州区校级期末)用配方法解方程x2+8x+7=0,则配方正确的是( )
A.(x+4)2=9B.(x﹣4)2=9C.(x﹣8)2=16D.(x+8)2=57
【解答】解:∵x2+8x+7=0,
∴x2+8x=﹣7,
⇒x2+8x+16=﹣7+16,
∴(x+4)2=9.
∴故选:A.
4.(2023秋•宝丰县期末)对甲、乙、丙、丁四名射击选手进行射击测试,每人射击10次,平均成绩均为9.5环,方差如表所示:则四名选手中成绩最稳定的是( )
A.甲B.乙C.两D.丁
【解答】解:因为乙的方差最小,所以乙的成绩最稳定;
故选:B.
5.(2022秋•陈仓区期末)一元二次方程x2+2x﹣1=0的根的情况是( )
A.只有一个实数根
B.有两个相等的实数根
C.有两个不相等的实数根
D.没有实数根
【解答】解:∵a=1,b=2,c=﹣1,
∴Δ=b2﹣4ac=22﹣4×1×(﹣1)=8>0,
∴一元二次方程x2+2x﹣1=0有两个不相等的实数根.
故选:C.
6.(2022秋•延边州期末)2022年北京冬奥会女子冰壶比赛,有若干支队伍参加了单循环比赛(每两队之间都赛一场),单循环比赛共进行了45场,共有多少支队伍参加比赛?设共有x支队伍参加比赛,则所列方程为( )
A.x(x+1)=45B.=45
C.x(x﹣1)=45D.=45
【解答】解:设共有x支队伍参加比赛,
依题意得:=45,
故选:D.
7.(2021秋•南宁期末)如图,在⊙O中,∠ABC=60°,则∠AOC的大小是( )
A.30°B.120°C.135°D.150°
【解答】解:∵∠AOC和∠ABC都对,
∴∠AOC=2∠ABC=2×60°=120°.
故选:B.
8.(2023秋•凉州区期末)工程上常用钢珠来测量零件上小孔的宽口,如果钢珠的直径为10mm,钢珠上顶端离零件上表面的距离为8mm,如图,则这个零件小孔的宽口AB等于( )mm.
A.4B.6C.7D.8
【解答】解:连接OA,过点O作OD⊥AB于点D,则AB=2AD,
∵钢珠的直径是10mm,
∴钢珠的半径是5mm,
∵钢珠顶端离零件表面的距离为8mm,
∴OD=3mm,
在Rt△AOD中,
∵AD===4(mm),
∴AB=2AD=2×4=8(mm).
故选:D.
二.填空题(共8小题)
9.(2024春•雁塔区校级期末)如图是由7个相同的小正方形和4个相同的大正方形组成的图形,在这个图形内任取一点P,则点P落在阴影部分的概率为 .
【解答】解:∵假设每个小正方形的面积都为1,总面积为4×4=16,其中阴影部分面积为1+9÷2=5.5,
∴点P落在阴影部分的概率是==.
故答案为:.
10.(2024春•西丰县期末)小明参加“强国有我”主题演讲比赛,其演讲形象、内容、效果三项的成绩分别是70分、90分、80分.若将三项得分依次按2:4:4的比例确定最终成绩,则小明的最终比赛成绩为 82 分.
【解答】解:小明的最终比赛成绩为(分).
故答案为:82.
11.(2024春•交城县期末)农科院计划为某地选择合适的甜玉米种子.选择种子时,甜玉米的产量和产量的稳定性是农科院所关心的问题.为了解甲、乙两种玉米的相关情况,农科院各用10块自然条件相同的试验田进行试验,得到数据如图.则甲、乙两种甜玉米产量的方差大小关系为 > .(填“<”或“>”)
【解答】解:从图中看到,甲种甜玉米产量的波动比乙的波动大,故甲的方差比乙大,即>.
故答案为:>.
12.(2023秋•崇仁县期末)若m,n为一元二次方程x2﹣2x﹣2=0的两个实数根,则(m+1)(n+1)的值为 1 .
【解答】解:∵m,n是一元二次方程x2﹣2x﹣2=0的两个实数根,
∴m+n=2,mn=﹣2,
∴(m+1)(n+1)
=mn+(m+n)+1
=﹣2+2+1
=1.
故答案为:1.
13.(2024春•蜀山区期末)为了节省材料,某农场水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为120米的围网在水库中围成了如图所示的①②③三块矩形区域,且这三块矩形区域的面积都为225平方米,则图中区域①矩形的长a为 30 米.
【解答】解:设图中区域①矩形的宽为x米,则图中区域②矩形的宽为2x米,图中区域①矩形的长a==(60﹣4x)米,
根据题意得:(60﹣4x)x=225,
整理得:4x2﹣60x+225=0,
解得:x1=x2=,
∴a=60﹣4x=60﹣4×=30.
故答案为:30.
14.(2023秋•仙游县期末)如图,正六边形ABCDEF内接于⊙O,⊙O的半径为6,则的长为 2π .
【解答】解:如图,连接OA,OB.
由题意OA=B=6,∠AOB=60°,
∴的长==2π.
故答案为:2π.
15.(2023秋•荣昌区校级期末)如图,▱ABCD中,边AB=2AD=8,∠BAD=45°,以A为圆心,对角线AD为半径画弧,分别交边AB于点E,连接EC,则图中阴影部分的面积是 .
【解答】解:过点D作DF⊥AB于点F,
∵AB=2AD=8,∠BAD=45°,
∴AD=4,AF=DF,
由勾股定理得:DF2+AF2=AD2,
∴DF==2,
∵AE=AD=4,
∴EB=AB﹣AE=8﹣4=4,
∴S阴影=S▱ABCD﹣S扇形ADE﹣S△EBC
=
=,
故答案为:.
16.(2023秋•崇义县期末)筒车是我国古代发明的一种水利灌溉工具,筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图1.唐代陈廷章在《水轮赋》中写道“水能利物,轮乃曲成”.如图2,已知圆心O在水面上方,且⊙O被水面截得弦AB长为8米,若点C为运行轨道的最低点,点C到弦AB所在直线的距离是2,则⊙O的半径长为 5 米.
【解答】解:连接OC交AB于点E.设OA=OC=r米,
由题意OC⊥AB,
∴(米),
∵CE=2,
∴OE=r﹣2,
在Rt△AEO中,r2=42+(r﹣2)2,
∴r=5米,
故答案为:5.
三.解答题(共8小题)
17.(2023秋•兰州期末)解方程:x2﹣6x+5=0(两种方法).
【解答】解:方法一:(x﹣5)(x﹣1)=0,
x﹣5=或x﹣1=0,
所以x1=5,x2=1;
方法二:x2﹣6x=﹣5,
x2﹣6x+9=4,
(x﹣3)2=4,
x﹣3=±2,
所以x1=5,x2=1.
18.(2024春•榆阳区期末)在一个不透明的袋子里,装有6个红球、3个黑球、1个白球,它们除颜色外都相同.
(1)求从袋中任意摸出一个球为红球的概率;
(2)现从袋中取走若干个红球,并放入相同数量的白球,充分摇匀后,要使从袋中随机摸出一个球是白球的概率是,问取走了多少个红球?
【解答】解:(1)从袋中任意摸出一个球有10种等可能结果,其中是红球的有6种结果,
所以从袋中任意摸出一个球为红球的概率为=;
(2)设取走了x个红球,
根据题意,得:=,
解得x=3,
答:取走了3个红球.
19.(2023秋•潼南区期末)已知关于x的一元二次方程mx2﹣2x﹣4=0有两个实数根.
(1)若方程的一个根是2,求m的值;
(2)求m的取值范围.
【解答】解:(1)把 x=2代入 mx2﹣2x﹣4=0 得:4m﹣4﹣4=0,
解得m=2;
(2)∵一元二次方程 mx2﹣2x﹣4=0 有两个实数根,
∴,
解得.
20.(2023秋•荣昌区校级期末)某商店销售一种成本为每千克40元的产品,根据市场分析,若按照每千克50元销售,一个月能售出这种产品500千克;销售单价每涨1元,月销售量就减少10千克.
(1)销售单价为58元时,这种产品的月销量是多少千克?
(2)该商店想在月销售成本不高于10000元的情况下,使得月销售利润达到8000元,销售单价应定为多少元?
【解答】解:(1)根据题意得:500﹣10×(58﹣50)
=500﹣10×8
=420(千克).
答:当销售单价为58元时,这种产品的月销量是420千克;
(2)设销售单价应定为x元,则每千克的销售利润为(x﹣40)元,月销售量为500﹣10(x﹣50)=(1000﹣10x)千克,
根据题意得:(x﹣40)(1000﹣10x)=8000,
整理得:x2﹣140x+4800=0,
∴(x﹣60)(x﹣80)=0,
∴x﹣60=0或x﹣80=0,
∴x=60或x=80,
当x=60时,40(1000﹣10x)=40×(1000﹣10×60)=16000>10000,不符合题意,舍去;
当x=80时,40(1000﹣10x)=40×(1000﹣10×80)=8000<10000,符合题意.
答:销售单价应定为80元.
21.(2023秋•东城区期末)如图,AB是⊙O的弦,半径OD⊥AB于点C.若AB=16,CD=2,求⊙O的半径的长.
【解答】解:如图,连接OA,
∵⊙O的弦AB=8,半径OD⊥AB,
∴AC=AB=×16=8,
设⊙O的半径为r,则OC=r﹣CD=r﹣2,
在Rt△OAC中,OA2=OC2+AC2,
即r2=(r﹣2)2+82,解得r=17.
故⊙O的半径的长为17.
22.(2023秋•盖州市期末)如图,已知△ABC,以AB为直径的⊙O分别交AC,BC于点D,E.连接DE,且ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=2.求CD的长.
【解答】(1)证明:∵ED=EC,
∴∠EDC=∠C,
∵∠EDC=∠B,(∵∠EDC+∠ADE=180°,∠B+∠ADE=180°,∴∠EDC=∠B)
∴∠B=∠C,
∴AB=AC;
(2)方法一:
解:连接AE,
∵AB为直径,
∴AE⊥BC,
由(1)知AB=AC,
∴BE=CE=BC=,
∵△CDE∽△CBA,
∴,
∴CE•CB=CD•CA,AC=AB=4,
∴•2=4CD,
∴CD=.
方法二:
解:连接BD,
∵AB为直径,
∴BD⊥AC,
设CD=a,
由(1)知AC=AB=4,
则AD=4﹣a,
在Rt△ABD中,由勾股定理可得:
BD2=AB2﹣AD2=42﹣(4﹣a)2
在Rt△CBD中,由勾股定理可得:
BD2=BC2﹣CD2=(2)2﹣a2
∴42﹣(4﹣a)2=(2)2﹣a2
整理得:a=,
即:CD=.
23.(2023秋•曲周县期末)在⊙O中,弦CD与直径AB相交于点P,∠ABC=63°.
(1)如图①,若∠APC=100°,求∠ABD;
(2)如图②,若CD⊥AB,过点D作⊙O的切线,与AB的延长线相交于点E,求∠E的大小.
【解答】解:(1)∵∠APC是△PBC的一个外角,∠ABC=63°,∠APC=100°,
∴∠C=∠APC﹣∠PBC=37°,
∵在⊙O中,∠BAD=∠C,
∵=,
∴∠BAD=37°,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠ABD=180°﹣∠BAD﹣∠ADB=180°﹣37°﹣90°=53°;
(2)如图,连接OD,
∵CD⊥AB,
∴∠CPB=90°,
∴∠PCB=90°﹣∠PBC=27°,
∵在⊙O中,∠BOD=2∠BCD,
∴∠BOD=54°,
∵DE是⊙O的切线,
∴OD⊥DE,即∠ODE=90°,
∴∠E=90°﹣∠EOD,
∴∠E=36°.
24.(2024春•红旗区校级期末)百度推出了“文心一言”AI聊天机器人(以下简称A款),抖音推出了“豆包”AI聊天机器人(以下简称B款).有关人员开展了A,B两款AI聊天机器人的使用满意度评分测验,并从中各随机抽取20份,对数据进行整理、描述和分析(评分分数用x表示,分为四个等级:不满意x<70,比较满意70≤x<80,满意80≤x<90,非常满意x≥90),下面给出了部分信息:
抽取的对A款AI聊天机器人的评分数据中“满意”的数据:
84,86,86,87,88,89;
抽取的对B款AI聊天机器人的评分数据:
66,68,69,81,84,85,86,87,87,87,88,89,95,97,98,98,98,98,99,100.
抽取的对A,B款AI聊天机器人的评分统计表
根据以上信息,解答下列问题:
(1)上述图表中a= 15 ,b= 88.5 ,c= 98 ;
(2)根据以上数据,你认为哪款AI聊天机器人更受用户喜爱?请说明理由(写出一条理由即可);
(3)在此次测验中,有240人对A款AI聊天机器人进行评分、300人对B款AI聊天机器人进行评分,请通过计算,估计此次测验中对AI聊天机器人不满意的共有多少人?
【解答】解:(1)由题意得:a%=1﹣10%﹣45%﹣×100%=15%,
即a=15,
∵A款的评分非常满意有20×45%=9(个),“满意”的数据为84、86、86、87、88、89,
∴把A款的评分数据从小到大排列,排在中间的两个数是88、89,
∴中位数b==88.5,
在B款的评分数据中,98出现的次数最多,
∴众数c=98;
故答案为:15,88.5,98;
(2)A款AI聊天机器人更受用户喜爱,理由如下:
因为两款的评分数据的平均数相同都是88,但A款评分数据的中位数为88比B款的中位数87高,所以A款AI聊天机器人更受用户喜爱(答案不唯一);
(3)=69(人),
答:估计此次测验中对AI聊天机器人不满意的大约共有69人.
选手
甲
乙
丙
丁
方差
1.34
0.16
2.56
0.21
设备
平均数
中位数
众数
“非常满意”所占百分比
A
88
b
96
45%
B
88
87
c
40%
选手
甲
乙
丙
丁
方差
1.34
0.16
2.56
0.21
设备
平均数
中位数
众数
“非常满意”所占百分比
A
88
b
96
45%
B
88
87
c
40%
相关试卷
这是一份2024-2025学年苏科版数学七年级上册 期末真题重组卷(模拟练习),共19页。
这是一份2024-2025学年人教版数学九年级上册期末模拟练习 (真题重组卷)-,共25页。
这是一份2024-2025学年人教版数学八年级上册期末 模拟练习 (真题重组卷),共24页。









