江苏无锡市东林中学2024-2025学年九上数学第12周阶段性训练模拟练习【含答案】

这是一份江苏无锡市东林中学2024-2025学年九上数学第12周阶段性训练模拟练习【含答案】，共26页。

A．70°B．72°C．74°D．76°
2．若关于x的一元二次方程ax2+k＝0的一个根为2，则二次函数y＝a（x+1）2+k与x轴的交点坐标为（ ）
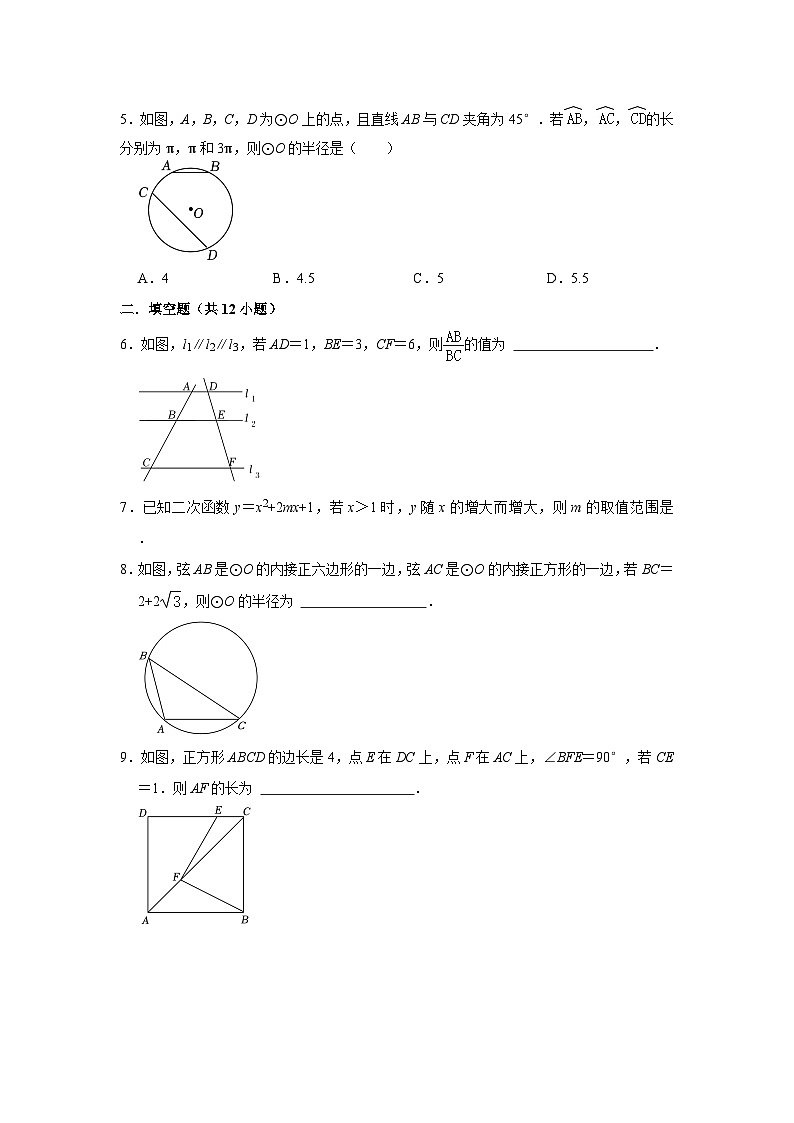
A．（﹣3，0）、（1，0）B．（﹣2，0）、（2，0）
C．（﹣1，0）、（1，0）D．（﹣1，0）、（3，0）
3．如图，在Rt△ABC，∠ACB＝90°，AC＝4，BC＝3，点D，E分别在AB，AC上，连接DE，将△ADE沿DE翻折，使点A的对应点F落在BC的延长线上，若FD平分∠EFB，则AD的长为（ ）
A．B．C．D．
4．如图，AB为⊙O的直径，PB，PC分别与⊙O相切于点B，C，过点C作AB的垂线，垂足为E，交⊙O于点D．若CD＝PB＝2，则BE长为（ ）
A．1B．2C．3D．4
5．如图，A，B，C，D为⊙O上的点，且直线AB与CD夹角为45°．若，，的长分别为π，π和3π，则⊙O的半径是（ ）
A．4B．4.5C．5D．5.5
二．填空题（共12小题）
6．如图，l1∥l2∥l3，若AD＝1，BE＝3，CF＝6，则的值为 ．
7．已知二次函数y＝x2+2mx+1，若x＞1时，y随x的增大而增大，则m的取值范围是 ．
8．如图，弦AB是⊙O的内接正六边形的一边，弦AC是⊙O的内接正方形的一边，若BC＝2+2，则⊙O的半径为 ．
9．如图，正方形ABCD的边长是4，点E在DC上，点F在AC上，∠BFE＝90°，若CE＝1．则AF的长为 ．
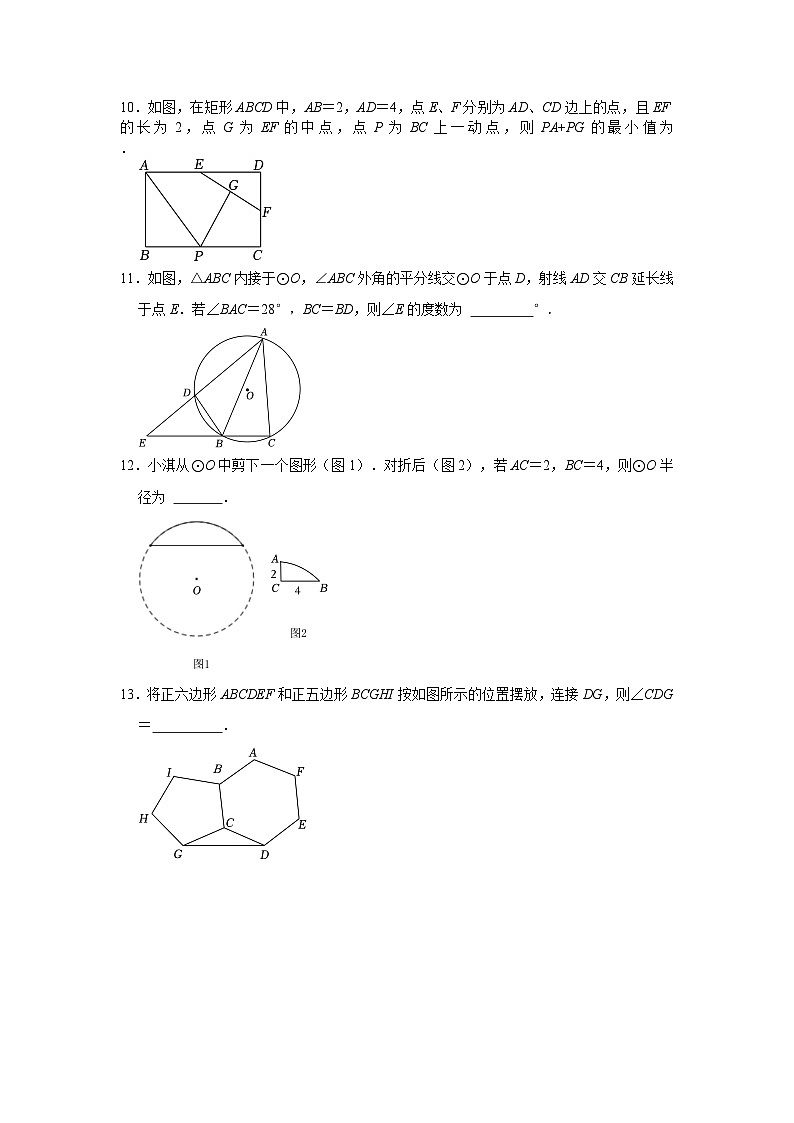
10．如图，在矩形ABCD中，AB＝2，AD＝4，点E、F分别为AD、CD边上的点，且EF的长为2，点G为EF的中点，点P为BC上一动点，则PA+PG的最小值为 ．
11．如图，△ABC内接于⊙O，∠ABC外角的平分线交⊙O于点D，射线AD交CB延长线于点E．若∠BAC＝28°，BC＝BD，则∠E的度数为 °．
12．小淇从⊙O中剪下一个图形（图1）．对折后（图2），若AC＝2，BC＝4，则⊙O半径为 ．
13．将正六边形ABCDEF和正五边形BCGHI按如图所示的位置摆放，连接DG，则∠CDG＝ ．
14．如图，△ABC中，∠ACB＝90°，AC＝3，BC＝4，CD是边E上的高，⊙E，⊙F分别是△ACD，△BCD的内切圆，则⊙E与⊙F的面积比为 ．
15．如图，△ABC是等边三角形，点P是边BC上的一点，且CP＞BP，以PC为边作等边△PCE．若△PAB的面积与△PCE的面积相等，则的值为 ．
16．如图，正五边形ABCDE内接于⊙O，AF是⊙O的直径，P是⊙O上的一点（不与点B，F重合），则∠BPF的度数为 °．
17．如图，在▱ABCD中，以CD为直径作⊙O，⊙O经过点A，且与BD交于点E，连接AE并延长，与BC交于点F，若F是BC的中点，AF＝6，则AB＝ ．
三．解答题（共6小题）
18．如图，AB为⊙O的直径，弦CD⊥AB于点P，连接BC，过点D作DE⊥CD，交⊙O于点E，连接AE，F是DE延长线上一点，且∠BCD＝∠FAE．
（1）求证：AF是⊙O的切线；
（2）若AF＝2，EF＝1，求⊙O的半径．
19．如图，四边形ABCD内接于⊙O，AB＝AC，BD⊥AC，垂足为E．
（1）求证：∠BAC＝2∠DAC；
（2）若AB＝10，CD＝5，求BC的值．
20．定义：圆心在三角形的一边上，与另一边相切，且经过三角形一个顶点（非切点）的圆，称为这个三角形圆心所在边上的“伴随圆”．
（1）如图①，在△ABC中，∠C＝90°，AB＝5，AC＝3，则BC边上的伴随圆的半径为 ．
（2）如图②，△ABC中，AB＝AC＝5，BC＝6，直接写出它的所有伴随圆的半径．
（3）如图③，△ABC中∠ACB＝90°，点E在边AB上，AE＝2BE，D为AC的中点，且∠CED＝90°．
①求证：△CED的外接圆是△ABC的AC边上的伴随圆；
②的值为 ．
21．一企业生产并销售某种产品（假设销量与产量相等），已知该产品每千克生产成本为40元，售价y（元）与产量x（kg）之间的函数关系为．
（1）当该产品产量为多少时，获得的利润最大？最大利润是多少？
（2）若企业每销售该产品1kg需支出其他费用a元（a＞0），当70≤x≤80时该企业获得的最大利润为2450元，求a的值．
22．如图，在△ABC中，CA＝CB，E为AB上一点，作EF∥BC，与AC交于点F，经过点A，E，F的⊙O与BC相切于点D，连接AD．
（1）求证：AD平分∠BAC；
（2）若AE＝5，BE＝4，求CD的长．
23．如图，在⊙O中，AB＝AC．
（1）若∠BOC＝100°，则的度数为 °；
（2）若AB＝13，BC＝10，求⊙O的半径．
参考答案与试题解析
一．选择题（共5小题）
1．【解答】解：如图，
，
∵∠OAC＝16°，∠OBC＝54°，
∴∠OBC﹣∠OAC＝54°﹣16°＝38°；
在△ADO和△BCD中，
∵∠ADO＝∠BDC，
∴∠AOB﹣∠ACB＝∠OBC﹣∠OAC＝38°，
∵∠AOB＝2∠ACB，
∴2∠ACB﹣∠ACB＝38°，
∴∠ACB＝38°，
∴∠AOB＝2∠ACB＝2×38°＝76°．
故选：D．
2．【解答】解：∵关于x的一元二次方程ax2+k＝0的一个根为2，
∴4a+k＝0，
解得k＝﹣4a，
把k＝﹣4a代入y＝a（x+1）2+k中，
得y＝a（x+1）2﹣4a，
当y＝0时，a（x+1）2﹣4a＝0，
即a（x+1）2＝4a，
∵a≠0，
∴（x+1）2＝4，
解得x＝1或x＝﹣3，
∴二次函数y＝a（x+1）2+k与x轴的交点坐标为（1，0）和（﹣3，0），
故选：A．
3．【解答】解：作DH⊥BC于H，
在Rt△ABC纸片中，∠ACB＝90°，
由勾股定理得：AB＝，
∵将△ADE沿DE翻折得△DEF，
∴AD＝DF，∠A＝∠DFE，
∵FD平分∠EFB，
∴∠DFE＝∠DFH，
∴∠DFH＝∠A，
设DH＝3x，
在Rt△DHF中，sin∠DFH＝sinA＝，
∴DF＝5x，
∴BD＝5﹣5x，
∵△BDH∽△BAC，
∴，
∴，
∴x＝，
∴AD＝5x＝．
故选：B．
4．【解答】解：作CH⊥PB于H，
∵直径AB⊥CD于H，
∴CE＝DE＝CD＝，
∵PC，PB分别切⊙O于C，B，
∴PB＝PC＝CD＝2，直径AB⊥PB，
∴四边形ECHB是矩形，
∴BH＝CE＝，BE＝CH，
∴PH＝PB﹣BH＝2﹣＝，
∴CH＝＝＝3，
∴BE＝CH＝3．
故选：C．
5．【解答】解：∵，，的长分别为π，π和3π，
∴的长为2π，的长为4π，
∴设弧长为π所对的圆周角为α，则∠BDC＝2α，∠ABD＝4α，
∵∠BDC+∠ABD+∠E＝180°，∠E＝45°，
∴2α+4α+45°＝180°，
∴α＝，
∴弧长为π所对的圆心角为×2＝45°，
∴＝π，
∴R＝4，
故选：A．
二．填空题（共12小题）
6．【解答】解：延长CA，FD交于点G，
∵l1∥l2，
∴，
∴AB＝BG﹣AG＝2AG，
∵l1∥l3，
∴，
∴BC＝CG﹣BG＝3AG，
∴，
故答案为：．
7．【解答】解：∵二次函数y＝x2+2mx+1，当x＞1时，y随x的增大而增大，
∴﹣≤1，
∴m≥﹣1，
故答案为m≥﹣1．
8．【解答】解：连接OA、OC，OA与BC交于点D，作OH⊥BC于H．
∵弦AB是⊙O的内接正六边形的一边，弦AC是⊙O的内接正方形的一边，
∴，，∠AOB＝60°，∠AOC＝90°，
∴OB＝OA＝AB＝r，AC＝OA＝，
∴AH＝＝，CH＝＝＝r，
∵BC＝2+2，
∴r+r＝2+2，
解得r＝2．
故答案为：2．
9．【解答】解：过点F作FG⊥CD于点G，交AB于点H，如图所示：
则∠EGF＝∠FHB＝90°，
∴∠GEF+∠GFE＝90°，
在正方形ABCD中，∠BCD＝∠ABC＝90°，∠ACD＝∠CAB＝45°，
∴四边形BCGH是矩形，
∴CG＝BH，
∵∠GCA＝45°，∠CGF＝90°，
∴∠GFC＝45°，
∴CG＝GF，
∴GF＝BH，
∵∠BFE＝90°，
∴∠GFE+∠HFB＝90°，
∴∠HFB＝∠GEF，
在△GFE和△HBF中，
，
∴△GFE≌△HBF（AAS），
∴FH＝GE，
∵∠CAB＝45°，∠AHF＝90°，
∴∠HFA＝45°，
∴AH＝FH，
设AH＝FH＝x，
∵正方形的边长为4，
∴AB＝4，
则GE＝x，HB＝4﹣x，
∵CG＝HB，
∴x+1＝4﹣x，
解得x＝，
∴AH＝FH＝，
在Rt△AFH中，根据勾股定理，得AF＝＝，
故答案为：．
10．【解答】解：∵EF＝2，点G为EF的中点，
∴DG＝1，
∴G是以D为圆心，以1为半径的圆弧上的点，
作A关于BC的对称点A′，连接A′D，PA′，
∵PA′+PG+DG≥A′D，
∴当D，G，P，A′共线时，PA+PG＝PA′+PG的值最小，
∵AB＝2，AD＝4，
∴AA′＝4，
∴A′D＝4，
∴PA+PG≥A′D﹣DG＝4﹣1；
∴PA+PG的最小值为4﹣1；
故答案为：4﹣1．
11．【解答】解：∵BC＝BD，
∴＝，
∴∠BAC＝∠BAD＝28°，
∴∠DAC＝∠BAC+∠BAD＝56°，
∵四边形ACBD是圆内接四边形，
∴∠DBC+∠DAC＝180°，
∵∠DBC+∠DBE＝180°，
∴∠DBE＝∠DAC＝56°，
∵BD平分∠ABE，
∴∠ABE＝2∠DBE＝112°，
∴∠E＝180°﹣∠ABE﹣∠BAD＝40°，
故答案为：40．
12．【解答】解：如图：连接OB，
由折叠得：∠OCB＝90°，
设⊙O半径为r，
∵AC＝2，
∴OC＝OA﹣OC＝r﹣2，
在Rt△OBC中，BC＝4，
∵BC2+OC2＝OB2，
∴42+（r﹣2）2＝r2，
解得：r＝5，
∴⊙O半径为5，
故答案为：5．
13．【解答】解：由题意得，CG＝CD．
∴∠CGD＝∠CDG．
∵多边形ABCDEF是正六边形、多边形BCGHI是正五边形．
∴∠BCG＝120°，∠BCD＝108°．
∴∠DCG＝360°﹣∠BCG﹣∠BCD＝360°﹣120°﹣108°＝132°．
∴∠CGD+∠CDG＝180°﹣∠GCD＝48°．
∴2∠CDG＝48°．
∴∠CDG＝24°．
故答案为：24°．
14．【解答】解：在△ABC中，
∵∠ACB＝90°，AC＝3，BC＝4，
∴AB＝＝5，
∵S△ABC＝AB•CD＝AC•BC，
∴CD＝，
在Rt△ACD中，由勾股定理得，
AD＝＝，
∴BD＝AB﹣AD＝，
设⊙E的半径为r，⊙F的半径为R，则
S△ACD＝AD•CD＝（AC+CD+AD）•r，
即×＝（3++）r，
∴r＝，
同理R＝，
∴⊙E与⊙F的面积比为＝＝，
故答案为：．
15．【解答】解：作AM⊥BC于M，EN⊥BC于N，设BP＝a，PC＝b，
∵△ABC是等边三角形，
∴AB＝BC＝a+b，
∵sin∠ABM＝，
∴AM＝AB•sin60°＝（a+b），
∴△ABP的面积＝+b）＝a（a+b），
∵△EPC等边三角形，
∴NE＝PE＝b，
∴△EPC的面积＝b×b＝b2，
∵△ABP的面积＝△EPC的面积，
∴a（a+b）＝b2，
∴a2+ab﹣b2＝0，
∴a＝b，或a＝b（舍），
∴＝，
∴＝．
故答案为：．
16．【解答】解：连接OC，OD，
∵正五边形ABCDE的五个顶点把圆五等分，
∴＝，
∴∠AOC＝∠AOD，
∴∠COF＝∠DOF，
∵OC＝OD，
∴直径AF⊥CD，
∴＝，
∵∠COD＝×360°＝72°，
∴∠COF＝＝36°，
当P在上时，连接OB，BP，FP，
∵∠BOC＝×360°＝72°，
∴∠BOF＝∠BOC+∠COF＝108°，
∴，
当P在上时，
由圆内接四边形的性质得∠BPF＝180°﹣54°＝126°．
∴∠BPF的度数是54°或126°．
故答案为：54或126．
17．【解答】解：连接AC，CE，
∵四边形ABCD是平行四边形，
∴AD∥BC，AD＝BC，
∵F是BC中点，
∴BF＝FC，
∵△BEF∽△DEA，
∴EF：EA＝BF：AD＝1：2，
∴EF＝AF＝×6＝2，
∵CD是⊙O的直径，
∴∠DEC＝∠DAC＝90°，
∴∠ACF＝∠DAC＝90°，∠BEC＝180°﹣∠DEC＝90°，
∴EF＝BF＝FC＝2，BC＝2EF＝4，
∵AC2＝AF2﹣FC2＝62﹣22＝32，
∴AB＝＝＝4．
故答案为：4．
三．解答题（共6小题）
18．【解答】（1）证明：如图，连接BE，
∵AB为⊙O的直径，
∴∠BEA＝90°，
∵CD⊥AB，
∴＝，
∴∠BCD＝∠BED，
∵∠BCD＝∠FAE，
∴∠BED＝∠FAE，
∵CD⊥AB，DE⊥CD，
∴AB∥ED，
∴∠BED＝∠ABE，
∴∠ABE＝∠FAE，
∵∠ABE+∠BAE＝90°，
∴∠FAE+∠BAE＝90°，
∴∠BAF＝90°，
∴OA⊥AF，
∵OA是⊙O的半径，
∴AF是⊙O的切线；
（2）解：∵∠APD＝∠D＝∠PAF＝90°，
∴四边形APDF是矩形，
∴∠AFE＝90°，
∵AF＝2，EF＝1，
∴AE＝＝，
∵∠F＝∠AEB＝90°，∠FAE＝∠EBA，
∴△FAE∽△EBA，
∴＝，
∴＝，
∴AB＝5，
∴OA＝AB＝．
∴⊙O的半径为．
19．【解答】（1）证明：∵BD⊥AC，
∴∠AEB＝∠BEC＝90°，
∴∠ACB＝90°﹣∠CBD，
∵AB＝AC，
∴∠ABC＝∠ACB＝90°﹣∠CBD，
∴∠BAC＝180°﹣2∠ABC＝2∠CBD，
∵∠DAC＝∠CBD，
∴∠BAC＝2∠DAC；
（2）解：过A作AH⊥BC于H，
∵AB＝AC，
∴∠BAH＝∠CAH＝CAB，CH＝BH，
∵∠BAC＝2∠DAC，
∴∠CAG＝∠CAH，
过C作CG⊥AD交AD的延长线于G，
∴∠G＝∠AHC＝90°，
∵AC＝AC，
∴△AGC≌△AHC（AAS），
∴AG＝AH，CG＝CH，
∵∠CDG＝∠ABC，
∴△CDG∽△ABH，
∴，
∴＝，
设BH＝k，AH＝2k，
∴AB＝＝k＝10，
∴k＝2，
∴BC＝2k＝4．
20．【解答】解：（1）∵BC是圆的切线，∠BCA＝90°，AC＝4，
∴AC为圆的直径．
∴AC边上的伴随圆的半径为2．
当伴随圆经过点C与AB相切时，设半径为r，则有r2+22＝（4﹣r）2
解得r＝1.5，
故答案为：2或1.5；
（2）当O在BC上时，如图（1）所示：连接OD，过点A作AE⊥BC．
∵AB＝AC，AE⊥BC，
∴BE＝EC＝3．
在△AEB中，由勾股定理可知AE＝＝4．
∵AB与⊙O相切，
∴OD⊥AB．
∴∠BDO＝∠BEA＝90°．
又∵∠OBD＝∠EBA，
∴△ODB∽△AEB．
∴．
设⊙O的半径为r．在OB＝6﹣r．
∴．
∴r＝．
∴△ABC的BC边上的伴随圆的半径为．
当O在AB上时，如图（2），连接OD、过点A作AE⊥BC，垂足为E．
∵BC与⊙O相切，
∴OD⊥BC．
又∵AE⊥BC，
∴OD∥AE．
∴△BOD∽△BAE．
∴．
设⊙O的半径为r，则OB＝5﹣r．
∴．
∴r＝．
如图（3）所示：连接OD、过点B作BF⊥AC，过点A作AE⊥BC，垂足为E．
∵S△ABC＝BC•AE＝AC•BF，
∴×6×4＝×5×BF．
∴BF＝4.8．
∵AC与⊙O相切，
∴DO⊥AC．
∴DO∥BF．
∴△AOD∽△ABF．
∴，即．
∴r＝．
综上所述，△ABC的伴随圆的半径分为或或；
（3）①证明：如图（4）连接OE、OB．
∵△CED为直角三角形，
∴△CED的外接圆圆心O在CD中点．
设⊙O的半径为r，则DC＝2r，OA＝3r．
∴．
∵EA＝2BE，
∴＝，
∴＝，
∴ED∥OB．
∴∠1＝∠2，∠3＝∠4．
又∵∠3＝∠2，
∴∠1＝∠4．
在△BCO和△BEO中，
，
∴△BCO≌△BEO（SAS）．
∴∠BEO＝∠BCO＝90°．
∴AB是圆O的切线．
∴△CED的外接圆是△ABC某一条边上的伴随圆．
②解：如图（4）设圆O的半径为r．
∵在Rt△OAE中，OA＝3r，OE＝r，
∴EA＝＝2r．
∴AB＝3r．
∵在Rt△ABC中，AC＝4r，AB＝3r，
∴BC＝＝r．
∵∠CED＝∠BCO＝90°，∠EDC＝∠1，
∴△DEC∽△OCB，
∴＝＝＝．
故答案为：．
21．【解答】解：（1）设当该产品产量为xkg时，获得的利润为w元，
根据题意，得w＝（﹣x+120﹣40）x＝﹣x2+80x＝﹣（x﹣80）2+3200，
∵，
∴当x＝80时，w有最大值，最大值为3200元，
答：当产品产量为80kg时，获得的利润最大，最大利润为3200元；
（2）设当产品产量为x千克时，获得的利润为P元．
根据题意，得，即，其中70≤x≤80．
该函数图象的对称轴为直线x＝80﹣a．
①若a＞10，则当x＝70时，P有最大值，即P＝3150﹣70a＜2450，
②若0＜a≤10，则当x＝80﹣a时，P有最大值，将x＝80﹣a代入，得．
当P＝2450时，．
解得a1＝10，a2＝150（不合题意，舍去）．
综上所述，a的值为10．
22．【解答】（1）证明：连接OD，
∵BC切⊙O于D，
∴半径OD⊥BC，
∵EF∥BC，
∴OD⊥EF，
∴＝，
∴∠BAD＝∠CAD，
∴AD平分∠BAC；
（2）解：连接DE，DF，
∵EF∥BC，
∴∠DEF＝∠EDB，
∵＝，
∴∠DEF＝∠BAD，
∴∠EDB＝∠BAD，
∵∠EBD＝∠ABD，
∴△BDE∽△BAD，
同理证明：△CDF∽△CAD，
∴BD：AB＝BE：BD，CD：CA＝CF：CD，
∴BD：（4+5）＝4：BD，
∴BD＝6，
∵EF∥BC，
∴AF：FC＝AE：EB＝5：4，
设CD＝x，
∴CA＝CB＝x+6，
∴CF＝（x+6），
∵CD2＝CF•CA，
∴x2＝（x+6）•（x+6），
∴x＝12，或x＝﹣（舍），
∴CD的长是12．
23．【解答】解：（1）∵在⊙O中，∠BOC＝100°，
∴∠BAC＝50°，
∵＝，
∴AB＝AC，
∴∠ABC＝∠ACB＝65°，
∴＝130°，
故答案为：130；
（2）连接AO，延长AO交BC于D，则AD⊥BC，BD＝CD＝BC＝5，
∴在直角△ABD中，由勾股定理，得AD＝＝＝12；
在直角△OBD中，由勾股定理，得OB2＝（12﹣OB）2+52，
解得OB＝，即⊙O的半径是．
声明：试题解析著作权属菁优网所有，未经书