江西省上饶市鄱阳县双港镇尧山中学2024-2025学年八年级上学期11月期中考试数学试题

这是一份江西省上饶市鄱阳县双港镇尧山中学2024-2025学年八年级上学期11月期中考试数学试题，共16页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
一、单选题（本大题共6小题，每小题3分，3×6＝18分）
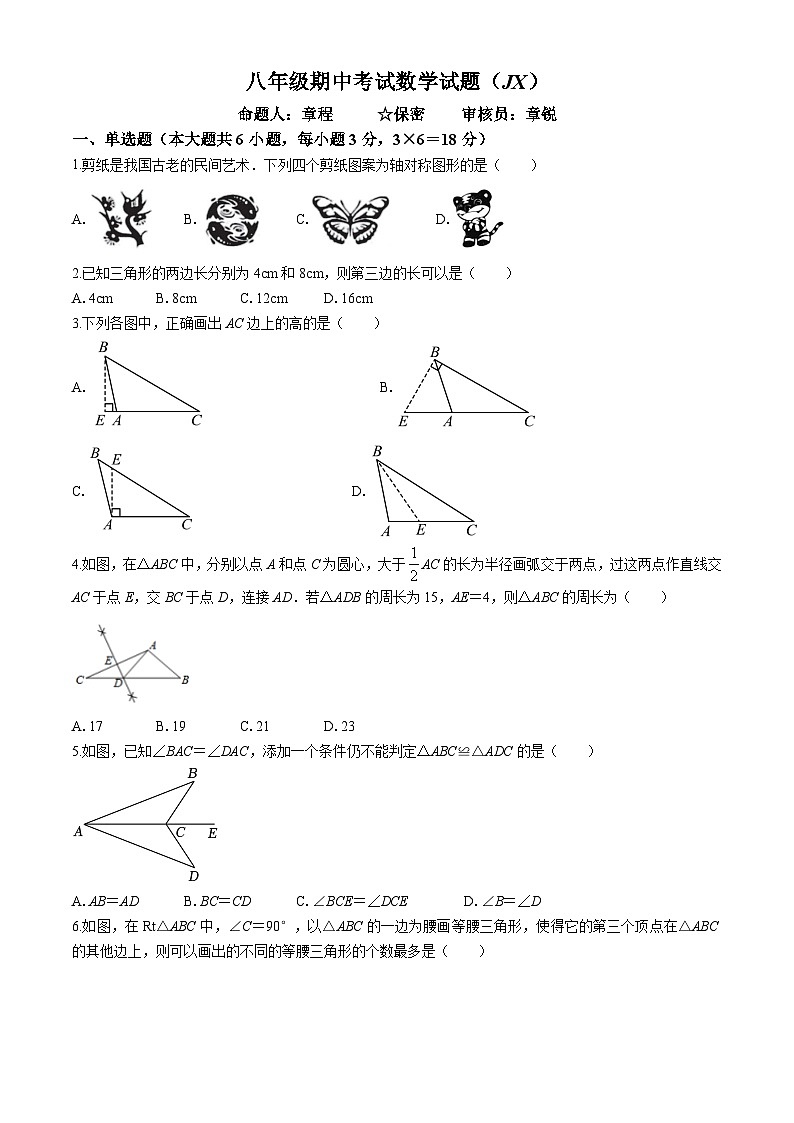
1.剪纸是我国古老的民间艺术．下列四个剪纸图案为轴对称图形的是（ ）
A.B.C.D.
2.已知三角形的两边长分别为4cm和8cm，则第三边的长可以是（ ）
A.4cmB.8cmC.12cmD.16cm
3.下列各图中，正确画出AC边上的高的是（ ）
A.B.
C.D.
4.如图，在△ABC中，分别以点A和点C为圆心，大于AC的长为半径画弧交于两点，过这两点作直线交AC于点E，交BC于点D，连接AD．若△ADB的周长为15，AE＝4，则△ABC的周长为（ ）
A.17B.19C.21D.23
5.如图，已知∠BAC＝∠DAC，添加一个条件仍不能判定△ABC≌△ADC的是（ ）
A.AB＝ADB.BC＝CDC.∠BCE＝∠DCE D.∠B＝∠D
6.如图，在Rt△ABC中，∠C＝90°，以△ABC的一边为腰画等腰三角形，使得它的第三个顶点在△ABC的其他边上，则可以画出的不同的等腰三角形的个数最多是（ ）
A.3个B.4个C.6个D.7个
二、填空题（本大题共6小题，每小题3分）
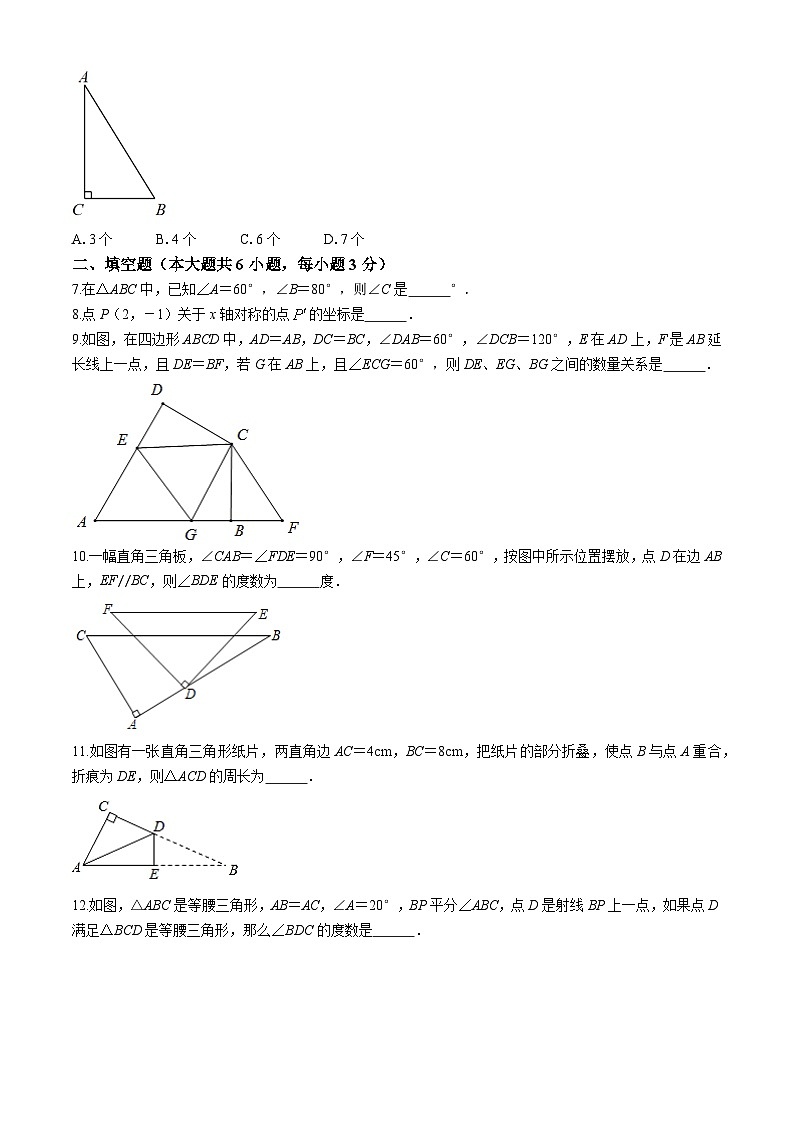
7.在△ABC中，已知∠A＝60°，∠B＝80°，则∠C是 °．
8.点P（2，－1）关于x轴对称的点的坐标是 ．
9.如图，在四边形ABCD中，AD＝AB，DC＝BC，∠DAB＝60°，∠DCB＝120°，E在AD上，F是AB延长线上一点，且DE＝BF，若G在AB上，且∠ECG＝60°，则DE、EG、BG之间的数量关系是 ．
10.一幅直角三角板，∠CAB＝∠FDE＝90°，∠F＝45°，∠C＝60°，按图中所示位置摆放，点D在边AB上，EF//BC，则∠BDE的度数为 度．
11.如图有一张直角三角形纸片，两直角边AC＝4cm，BC＝8cm，把纸片的部分折叠，使点B与点A重合，折痕为DE，则△ACD的周长为 ．
12.如图，△ABC是等腰三角形，AB＝AC，∠A＝20°，BP平分∠ABC，点D是射线BP上一点，如果点D满足△BCD是等腰三角形，那么∠BDC的度数是 ．
三、解答题（本大题共11小题，共84分，以6，6，6，6，6，8，8，8，9，9，12打分）
13.如图，在△ABC中，AE是∠BAC的平分线，交BC于点E，DE//AB交AC于点D．求证：AD＝ED．
14.等腰三角形两条边长分别为6和10，求这个等腰三角形的周长．
15.如图，在△ABC中，AB＝AC，CD平分∠ACB，交AB于点D．
（1）过点B作BE⊥直线CD于点E．（要求：尺规作图，保留作图痕迹，不写作法）
（2）∠ABE与∠ACE之间有何数量关系？请说明理由．
16.如图，在Rt△ABC中，试利用直尺和圆规作图（不写作法，保留作图痕迹）．
（1）在BC边上求作一点P，使得点P到AB的距离等于PC的长；
（2）作出（1）中过点P垂直于AB的垂线段PD．
17.如图，已知AB＝BC，∠BCD＝∠ABD，点E在BD上，BE＝CD．求证：AE＝BD．
18.如图，已知线段AB＝2cm，其垂直平分线CD的作法如下：
（1）分别以点A和点B为圆心，bcm长为半径画弧，两弧相交于C，D两点；
（2）作直线CD．
上述作法中，b的值需要满足的条件为b 1（填“＞”“＜”或“＝”）．
19.如图，△ABC三个顶点的坐标分别为A（1，1）、B（4，2），C（3，4）．
（1）若与△ABC关于y轴成轴对称，请在网格中画出，并写出三顶点坐标： ， ， ；
（2）计算△ABC的面积；
（3）若点P为x轴上一点，当PA＋PB最小时，写出此时P点坐标 ．
20.证明命题“等腰三角形两腰上的高相等”，要根据题意，画出图形，并用符号表示已知和求证，写出证明过程，下面是小明根据题意画出的图形，并写出不完整的已知和求证．
已知：如图，在△ABC中，AB＝AC， ．
求证： ．
请补全已知和求证部分，并写出证明过程．
21.如图，过△ABC的边BC的垂直平分线DG上的点D作△ABC另外两边AB，AC所在的直线的垂线，垂足分别为E、F，且BE＝CF．求证：
（1）DF＝DE；
（2）若∠A＝30°，CD＝6，请你求出△DCB的面积．
22.【情境再现】甲、乙两个含45°角的直角三角尺如图（1）放置，甲的直角顶点放在乙斜边上的高的垂足O处．将甲绕点O顺时针旋转一个锐角到图（2）位置．小莹用作图软件GeGebra按图（2）作出示意图，并连接AG，BH，如图（3）所示，AB交HO于E，AC交OG于F，通过证明△OBE≌△OAF，可得OE＝OF．
图（1） 图（2） 图（3）
请你证明：AG＝BH．
【迁移应用】延长GA分别交HO，HB所在直线于点P，D，如图（4），猜想并证明DG与BH的位置关系．
图（4）
23.如图所示，在△ABC中，AB＝8，AC＝4，点G为BC的中点，DG⊥BC交∠BAC的平分线AD于点D，DE⊥AB于点E， DF⊥AC交AC的延长线于点F．
（1）求证：BE＝CF；
（2）求AE的长．
评分建议与学生理解解析
1.【答案】C
【解析】A选项，不是轴对称图形，本选项不符合题意；B选项，不是轴对称图形，本选项不符合题意；C选项，是轴对称图形，本选项符合题意；D选项，不是轴对称图形，本选项不符合题意．故选C．
2.【答案】B
【详解】解：设第三边的长为xcm，
由题意可得，8－4＜x＜8＋4，
∴4＜x＜12，
故此题答案为B．
3.【答案】A
【分析】直接根据高线的定义即可得出结论．
【详解】解：A、BE是AC边上的高，符合题意；
B、BE不是AC边上的高，不符合题意；
C、AE不是AC边上的高，不符合题意；
D、BE不是AC边上的高，不符合题意；
故此题答案为：A．
【关键点拨】此题考查了三角形的高，熟知三角形高线的作法是解题的关键．
4.【答案】D
【分析】由题意知，DE是线段AC的垂直平分线，据此得AD＝CD，AE＝EC，再由AB＋BD＋AD＝15知AB＋BD＋ CD＝15，即AB＋BC＝15，结合AE＝4可得答案．
【详解】解：由题意知，DE是线段AC的垂直平分线，
∴AD＝CD，AE＝EC，
∵AB＋BD＋AD＝15，
∴AB＋BD＋CD＝15，即AB＋BC＝15，
∵AE＝4，即AC＝2AE＝8，
∴△ABC的周长为AB＋BC＋AC＝15＋8＝23，
故选：D．
【点晴】本题主要考查作图一基本作图，线段垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．
5.【答案】B
【分析】本题考查了全等三角形的判定；根据全等三角形的判定定理逐项判断即可．
【详解】解：由题意得：∠BAC＝∠DAC，AC＝AC，
A.若添加AB＝AD，根据全等三角形判定定理SAS判定△ABC≌△ADC，故不符合题意；
B．若添加BC＝CD，不能根据全等三角形判定定理判定△ABC≌△ADC，故符合题意；
C．若添加∠BCE＝∠DCE，根据平角定义可以得出∠ACB＝∠ACD，然后根据全等三角形判定定理ASA能判定△ABC≌△ADC，故不符合题意；
D．若添加∠B＝∠D，根据全等三角形判定定理AAS能判定△ABC≌△ADC，故不符合题意；
故此题答案为：B．
6.【答案】C
【分析】根据等腰三角形的定义，分别以A、B、C三个顶点为等腰三角形的顶点可以画出4个等腰三角形，分别以三条边等腰三角形的底边可以作出3个等腰三角形，最多可以作出7个不同的等腰三角形．
【详解】①以B为圆心，BC长为半径画弧，交AB于点D，△BCD是等腰三角形，
图1
②以A为圆心，AC长为半径画弧，交AB于点E，△ACE就是等腰三角形；
图2
③以C为圆心，BC长为半径画弧，交AC于点F，△BCF就是等腰三角形，交AB于点，是等腰三角形；
图3
④作AC的垂直平分线交AB于点H，△ACH就是等腰三角形；
图4
⑤作AB的垂直平分线交AC于G，则△AGB是等腰三角形；
图5
⑥作BC的垂直平分线交AB于I，则△BCI和△ACI都是等腰三角形，此情形点H与点I重合与④的情形重合，共计2个等腰三角形．
图6
综上所述，最多有7个等腰三角形．
故此题答案为D．
【关键点拨】此题考查了等腰三角形的定义，分类讨论是解题的关键．
7.【答案】40
【分析】根据三角形内角和定理计算即可．
【详解】解：∵∠A＝60°，∠B＝80°，
∴∠C＝180°－60°－80°＝40°，
故答案为：40
【点晴】本题考查三角形内角和定理，三角形内角和是180°．
8.【答案】（2，1）
【分析】根据关于x轴对称的点的坐标特征是横坐标相同，纵坐标互为相反数，可知的点坐标．
【详解】解：由题意知点P（2，－1）关于x轴对称的点的坐标是（2，1）
9.【答案】DE＋BG＝EG
【分析】连接AC，利用全等三角形的判定和性质，求解即可．
【详解】解：猜想DE、EG、BG之间的数量关系为：DE＋BG＝EG． 理由如下：
连接AC，如图所示，
在△ABC和△ADC中，
∴△ABC≌△ADC（SSS），
∴∠BCA＝∠DCA＝∠DCB＝60°
又∵∠ECG＝60°，
∴∠DCE＝∠ACG，∠ACE＝∠BCG，
∵∠D＋∠DAB＋∠ABC＋∠DCB＝360°，∠DAB＝60°，∠DCB＝120°，
∴∠D＋∠ABC＝360°－60°－120°＝180°，
又∵∠CBF＋∠ABC＝180°，
∴∠D＝∠CBF，
在△CDE和△CBF中，
∴△CDE≌△CBF（SAS），
∴CE＝CF，∠DCE＝∠BCF，
∴∠BCG＋∠BCF＝∠ACE＋∠DCE＝60°，即∠FCG＝60°，
∴∠ECG＝∠FCG，
在△CEG和△CFG中，
∴△CEG≌△CFG（SAS），
∴EG＝FG，
又∵DE＝BF，FG＝BF＋BG，
∴DE＋BG＝EG
故此题答案为：DE＋BG＝EG
【关键点拨】此题考查了全等三角形的判定与性质，解题的关键是熟练掌握全等三角形的判定方法与性质．
10.【答案】15
【分析】依据平行线的性质，即可得到∠CGD的度数，再根据三角形外角的性质，即可得到∠BDE的度数．
【详解】解：如图所示，设CB与ED交点为G，
∵∠CAB＝∠FDE＝90°，∠F＝45°，∠C＝60°，
∴∠E＝90°－∠F＝45°，∠B＝90°－∠C＝30°，
∵EF∥BC，
∴∠E＝∠CGD＝45°，
又∵∠CGD是△BDG的外角，
∴∠CGD＝∠B＋∠BDE，
∴∠BDE＝45°－30°＝15°，
故此题答案为：15
【关键点拨】此题主要考查了平行线的性质以及三角形外角性质，解题时注意：两条平行线被第三条直线所截，同位角相等．
11.【答案】12cm
【分析】根据折叠的性质得到AD＝BD，根据三角形的周长公式计算，得到答案．
【详解】解：由折叠的性质可知，AD＝BD，
∴△ACD周长＝AC＋CD＋AD＝AC＋CD＋DB＝AC＋BC＝12（cm）．
12.【答案】40°或70°或100°
【解析】①当BC＝CD时，如图（1）所示．∵∠A＝20°，AB＝AC，∴∠ABC＝80°．∵BP平分∠ABC，∴∠CBD＝40°．∵BC＝CD，∴∠CBD＝∠BDC＝40°．
②当BD＝BC时，如图（2）所示．由①可知∠CBD＝40°．∵BD＝BC，∴∠BDC＝70°．
③当DB＝DC时，如图（3）所示．由①可知∠CBD＝40°．∵BD＝CD，∴∠BDC＝100°．
故答案为40°或70°或100°．
图（1） 图（2） 图（3）
【易错警示】本题中未给出D点位置，所以需要对D点位置进行分类讨论，避免漏解．
13.【答案】见解析
【分析】根据AE是∠BAC的平分线，可得∠CAE＝∠BAE，再由DE//AB，可得∠AED＝∠BAE ，从而得到∠AED ＝∠CAE，即可求证．
【详解】证明：∵AE是∠BAC的平分线，
∴∠CAE＝∠BAE，
∵DE∥AB，
∴∠AED＝∠BAE，
∴∠AED＝∠CAE，
∴AD＝ED．
【点睛】本题主要考查了等腰三角形的判定，平行线的性质，熟练掌握等腰三角形的判定定理是解题的关键．
14.【答案】这个等腰三角形的周长为22或26
【分析】分类讨论，分别求出①腰长为6，②腰长为10时三角形的周长，并根据三角形的三边关系进行判断．
【详解】腰长为6时，三边为6、6、10，能构成三角形，
三角形的周长＝6＋6＋10＝22；
腰长为10时，三边为10、10、6，能构成三角形，
三角形的周长＝10＋10＋6＝26
故答案为：22或26
【点睛】本题主要考查等腰三角形的性质，关键在于分类讨论思想以及三角形三边关系的应用．
15.【答案】（1）见解析
（2）∠ABE＝90°－3∠ACE．理由见解答
【分析】（1）以点B为圆心，适当长为半径画弧，交直线CD于两点，以这两点为圆心，大于这两点距离的一半为半径画弧，交BC的上方于一点，作过这点和点B的直线交CD于点E；
（2）根据角平分线的定义，三角形内角和定理即可求解．
【详解】（1）如图，BE即为所求．
（2）∠ABE＝90°－3∠ACE．
理由：∵CE平分∠ACB，
∴∠BCE＝∠ACE，∠ACB＝2∠ACE．
∵AB＝AC，
∴∠ABC＝∠ACB＝2∠ACE．
∵BE⊥CD，
∴∠BEC＝90°，
∴∠ABE ＝90°－∠BCE－∠ABC＝90°－∠BCE－∠ACB＝90°－3∠ACE．
16.【答案】（1）见解析
（2）见解析
【分析】（1）作∠A的角平分线，角平分线与线段BC的交点即为所求．
（2）根据作线段垂直平分线的方法作图即可．
【详解】（1）解：作∠A的角平分线，角平分线与线段BC的交点即为所求．
（2）PD即为所求作的垂线段．
17.【答案】见解析
【分析】根据题目中的条件和全等三角形判定的方法，可以写出△ABE≌△BCD成立的条件，然后即可得到AE＝BD．
【详解】证明：∵∠BCD＝∠ABD，
∴∠BCD＝∠ABE，
在△ABE和△BCD中，
∴△ABE≌△BCD（SAS），
∴AE＝BD．
【点睛】本题考查全等三角形的判定与性质，解答本题的关键是明确题意，利用数形结合的思想解答．
18.【答案】＞
【详解】∵AB＝2cm，b＞AB，∴b＞1 故答案为：＞．
【关键点拨】线段AB 的垂直平分线的作图方法为以A，B为圆心，大于AB为半径画弧，两弧交于C，D两点，作直线CD．
19.【答案】（1）（－1，1），（－4，2），（－3，4）
（2）3.5
（3）（2，0）
【分析】（1）依据轴对称的性质进行作图，即可得到，进而得出三顶点坐标；
（2）依据割补法进行计算，即可得到△ABC的面积；
（3）作点A关于x轴的对称点Q，连接QB，交x轴于点P，依据一次函数的图象可得点P的坐标．
（1）如图，即为所求；
其中的坐标分别为：
故答案为：（－1，1），（－4，2），（－3，4）
（2）△ABC的面积为：．
（3）
如图，作点A关于x轴的对称点Q，连接QB，则QB与x轴的交点即是点P的位置．
设QB的解析式为，
把Q（1，－1）和B（4，2）代入可得：
，解得
令，则，
∴P点坐标为（2，0），
故答案为：（2，0）．
【点睛】本题考查了作图—轴对称变换、轴对称一最短路线问题，解决本题的关键是掌握轴对称的性质．凡是涉及最短距离的问题，一般要考虑线段的性质定理，结合轴对称变换来解决，多数情况要作点关于某直线的对称点．
20.【答案】见解析
【分析】证明△BEC≌△CDB，根据全等三角形的性质即可求解．
【详解】解答：
已知：CE⊥AB，BD⊥AC；
求证：CE＝BD．
证明过程：∵AB＝AC
∴∠ABC＝∠ACB．
∵CE⊥AB，BD⊥AC
∴∠BEC＝∠CDB，
又BC＝BC
∴△BEC≌△CDB（ASA），
∴CE＝BD．
【关键点拨】考查等腰三角形的性质以及全等三角形的判定与性质，掌握全等三角形的判定定理是解题的关键．
21.【答案】（1）证明见解析
（2）9
【分析】此题考查了线段垂直平分线的性质，全等三角形的判定和性质，含30°的直角三角形的性质，解题关键是利用HL证明Rt△CDF≌Rt△BDE．
（1）根据线段的垂直平分线的性质得出CD＝BD，利用HL证明Rt△CDF≌Rt△BDE，得到CF＝BE；
（2）先证明∠BDE＝30°，可得BE＝CF＝3，再利用三角形的面积公式计算即可．
【详解】（1）证明：∵D在BC的垂直平分线上，
∴CD＝BD，
∵DE⊥AB，DF⊥AC，
∴∠DFC＝90°，∠DEB＝90°，
∴△CDF和△BDE为直角三角形，
在Rt△CDF和Rt△BDE中，
∴Rt△CDF≌Rt△BDE（HL）
∴DF＝DE；
（2）∵∠A＝30°，AF⊥BF，
∴∠ABF＝60°，而DE⊥AB，
∴∠BDE＝30°，
∵CD＝BD＝6，
∴BE＝CF＝3，
∴．
22.【答案】【情境再现】【证明】由材料知△OBE≌△OAF∴BE＝AF，OE＝OF，∠BEO＝∠AFO，∴∠BEH＝∠AFG．∵OH＝OG，
∴OH－OE＝OG－OF，即EH＝GF．
在△BHE和△AGF中，
∴△BHE≌△AGF，∴BH＝AG．
【迁移应用】【解】猜想：DG⊥BH．证明如下：
由【情境再现】知，△ BHE≌△AGF，∴∠BHE＝∠AGF．
∵∠HOG＝90°，∴∠AGF＋∠GPO＝90°，
∴∠BHE＋∠GPO＝90°．∵∠GPO＝∠HPD，∴∠BHE＋∠HPD＝90°，
∴∠HDP＝90°，∴DG⊥BH．
23.【答案】（1）证明见解析
（2）6
【分析】（1）如图所示，连接BD，CD，先利用SAS证明△BGD≌△CGD得到BD＝CD，再由角平分线的性质得到DE＝DF，即可利用HL证明Rt△DEB≌Rt△DFC则BE＝CF；
（2）证明Rt△ADE≌Rt△ADF（HL），得到AF＝AE，由（1）得BE＝CF，则AE＝AF＝AC＋CF，据此求出BE的长，即可求出AE的长．
【详解】（1）解：如图所示，连接BD，CD，
∵G是BC的中点，DG⊥BC，
∴BG＝CG，∠BGD＝∠CGD＝90°，
又∵DG＝DG
∴△BGD≌△CGD（SAS），
∴BD＝CD，
∵AD平分∠BAC，DE⊥AB，DF⊥AC，
∴DE＝DF，∠DEB＝∠DFC＝90°，
又∵DB＝DC，
∴Rt△DEB≌Rt△DFC（HL），
∴BF＝CF；
（2）解：在Rt△ADE和Rt△ADF中，
∴Rt△ADE≌Rt△ADF（HL），
∴AF＝AE
由（1）得BE＝CF，
∴AE＝AF＝AC＋CF，
∴AB＝AE＋BE＝AC＋CF＋BE＝AC＋2BE，
∵AB＝8，AC＝4，
∴BE＝2，
∴AE＝AB－BE＝6