
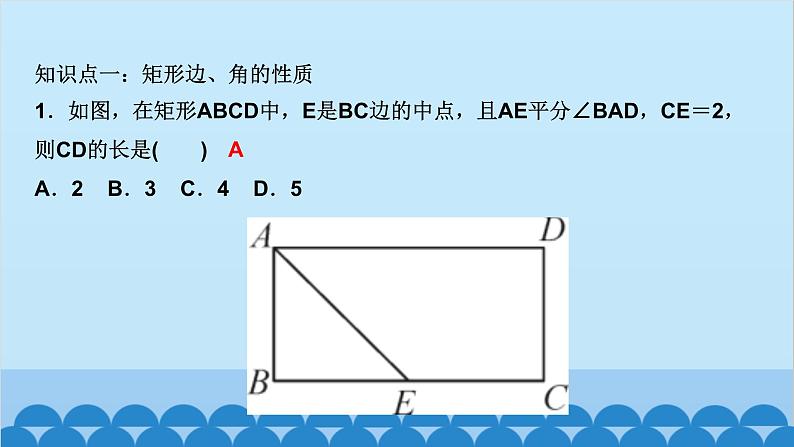
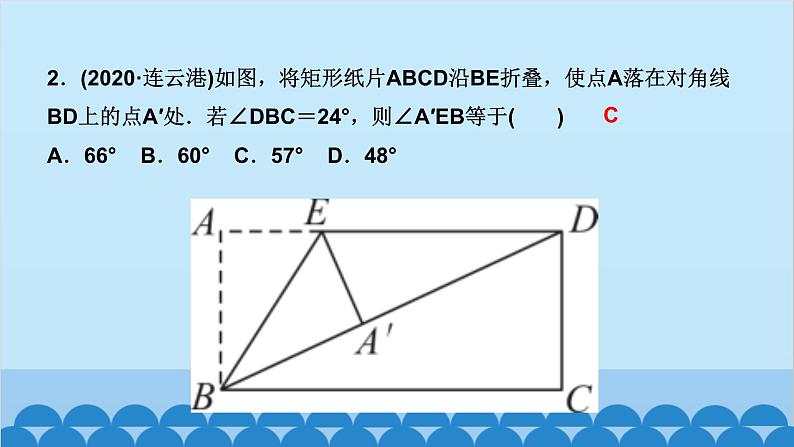
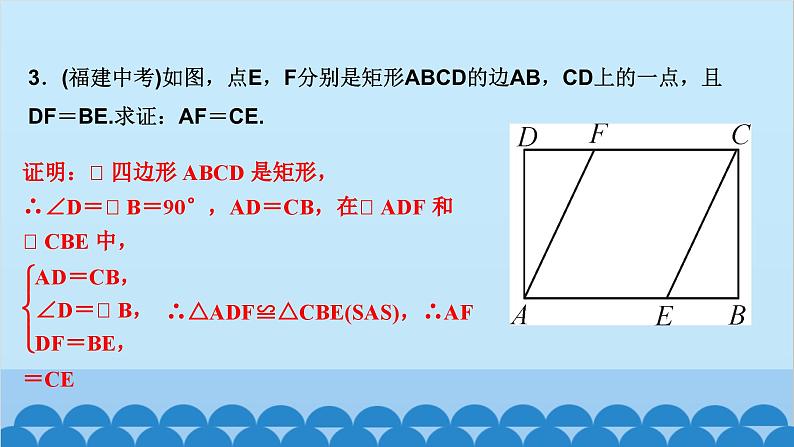

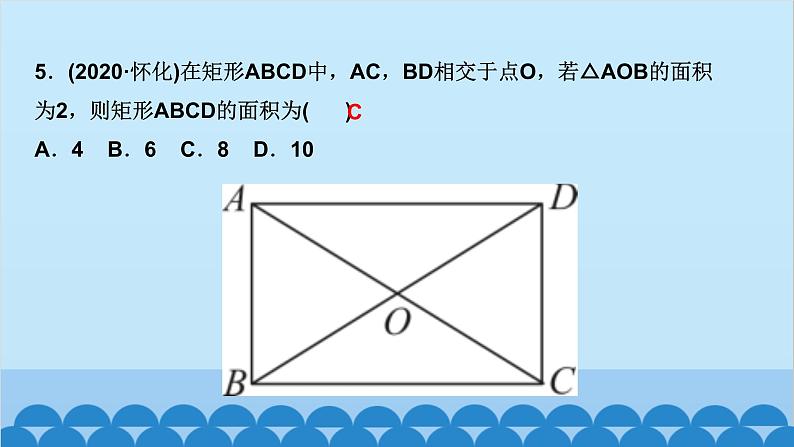















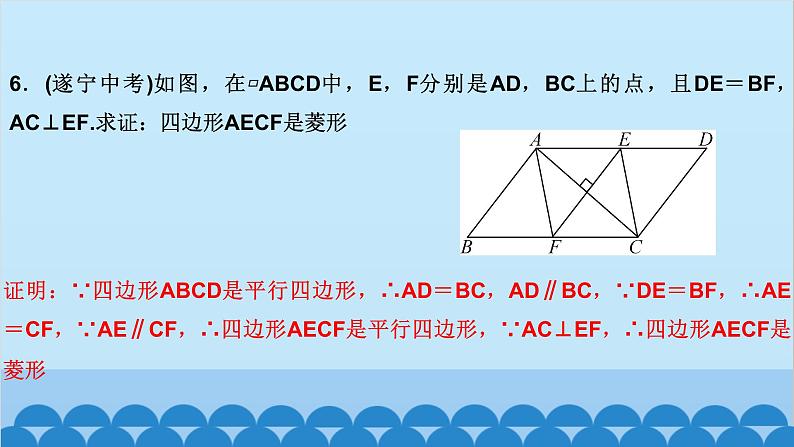
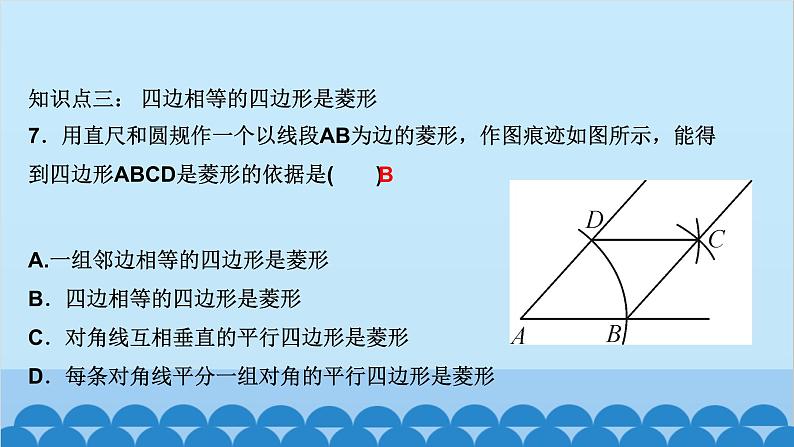


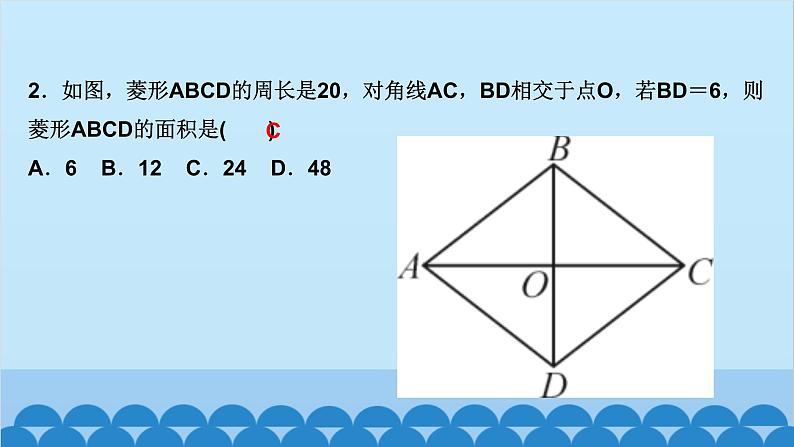

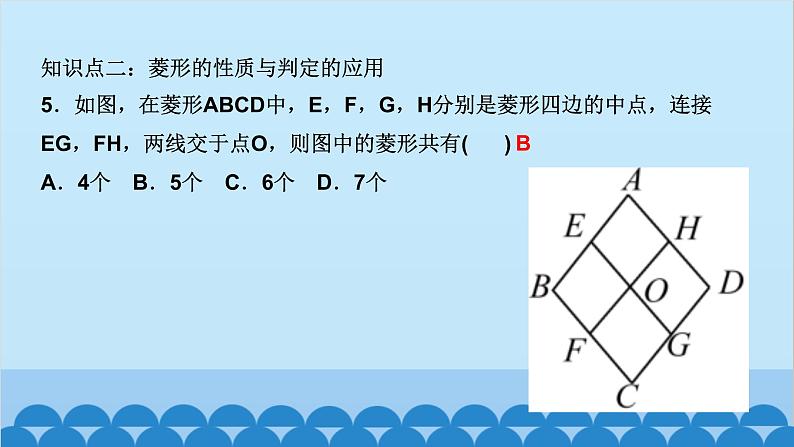
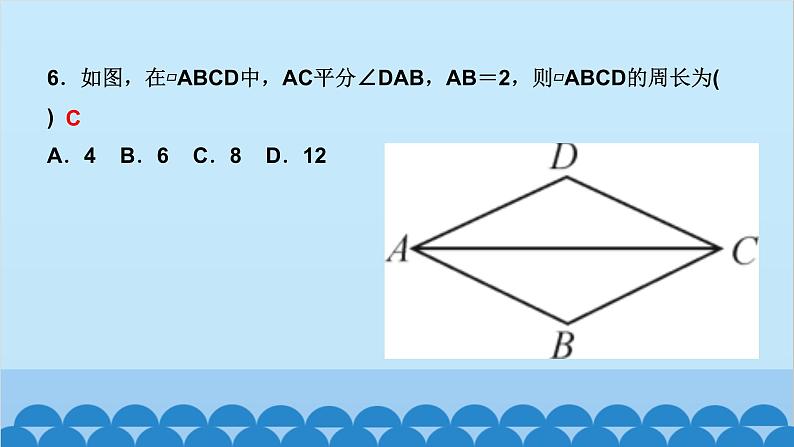
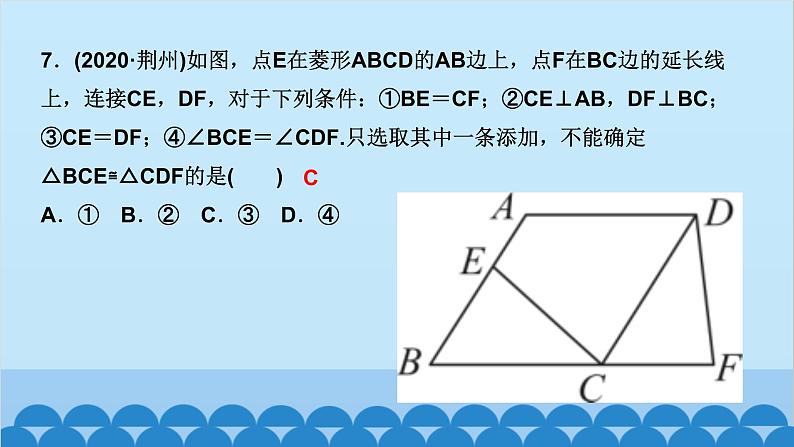
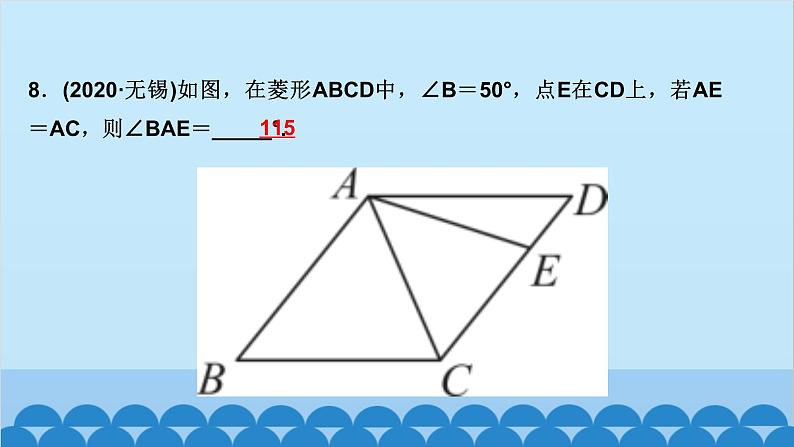


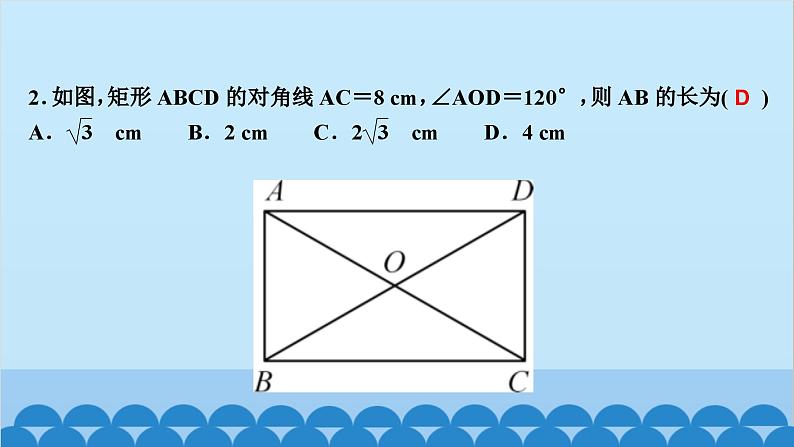






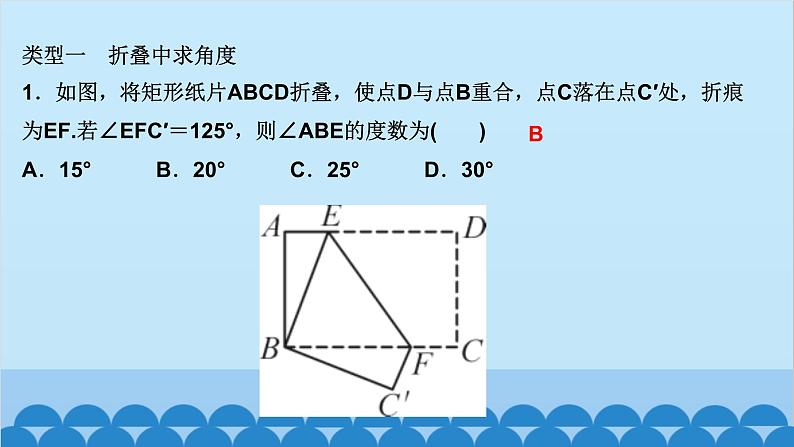
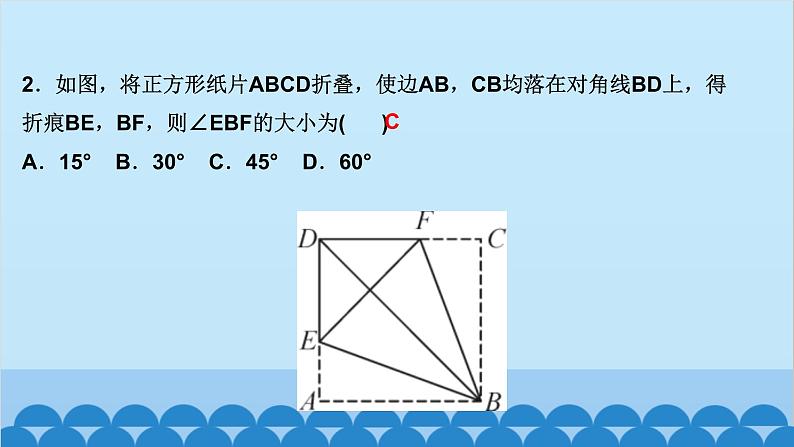
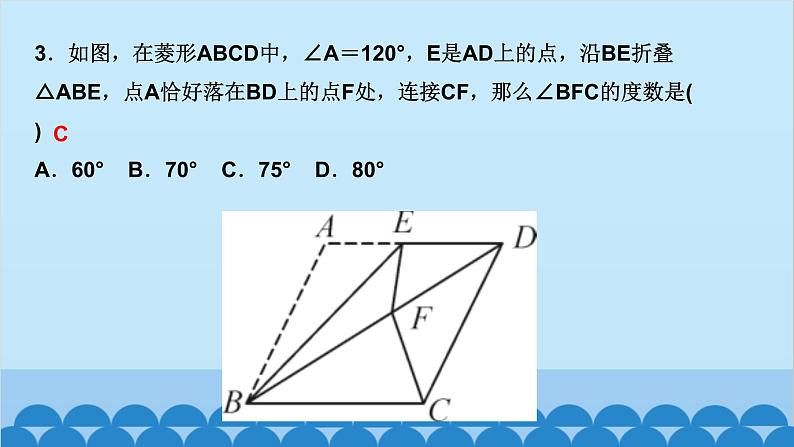
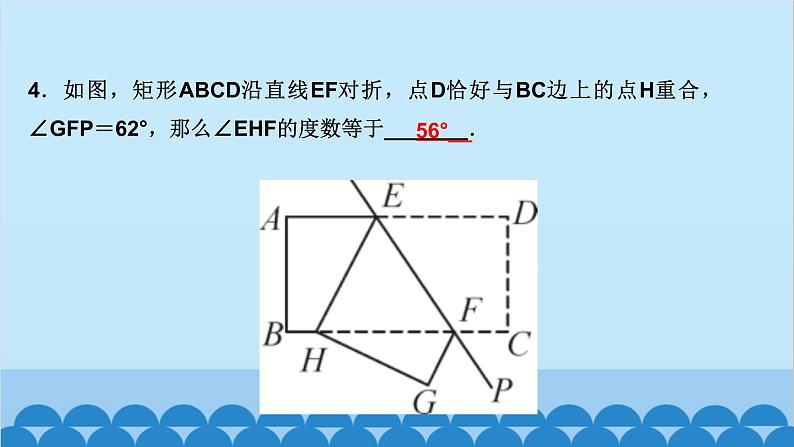


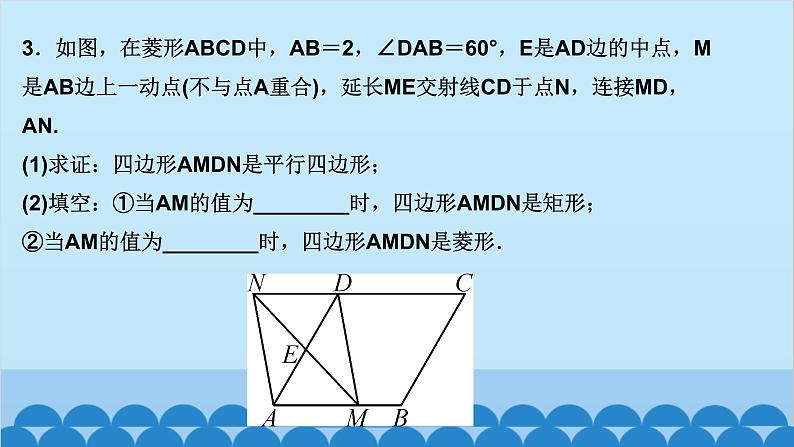

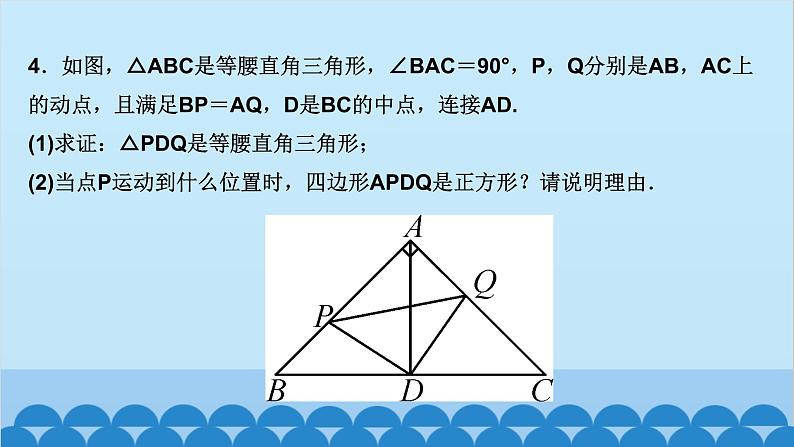
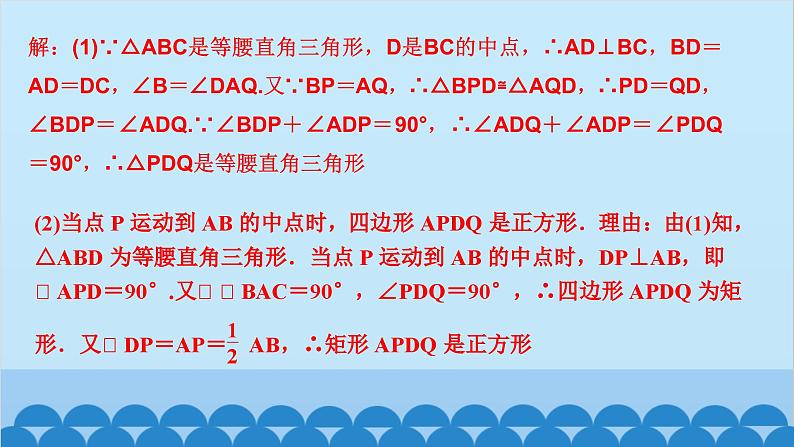






所属成套资源:北师大版数学九年级上册习题课件
北师大版数学九年级上册 第一章 特殊平行四边形习题课件
展开
这是一份北师大版数学九年级上册 第一章 特殊平行四边形习题课件,文件包含12矩形的性质与判定第1课时矩形的性质ppt、11菱形的性质与判定第1课时菱形的性质ppt、13正方形的性质与判定第1课时正方形的性质ppt、12矩形的性质与判定第2课时矩形的判定ppt、13正方形的性质与判定第2课时正方形的判定ppt、11菱形的性质与判定第2课时菱形的判定ppt、11菱形的性质与判定第3课时菱形的性质与判定的综合运用ppt、12矩形的性质与判定第3课时矩形性质和判定的运用ppt、单元复习一特殊平行四边形ppt、专题课堂二特殊平行四边形中的折叠问题ppt、专题课堂一特殊平行四边形的应用ppt、易错课堂一特殊平行四边形ppt等12份课件配套教学资源,其中PPT共205页, 欢迎下载使用。
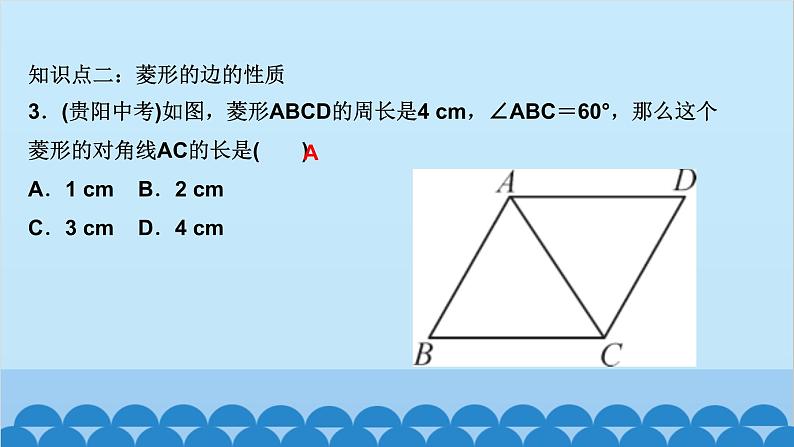
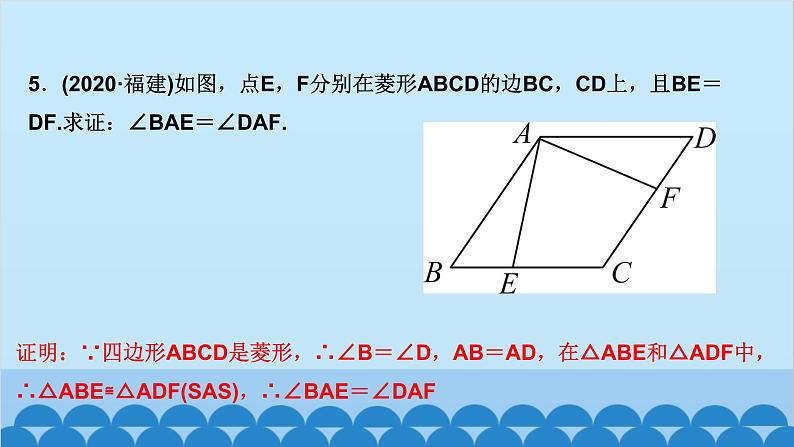
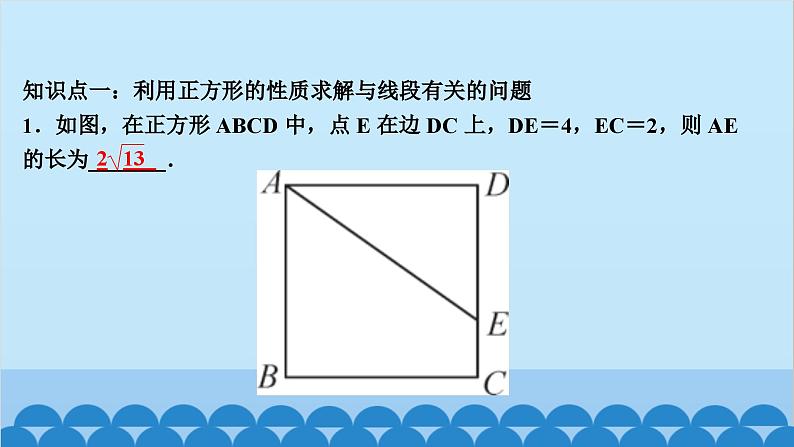
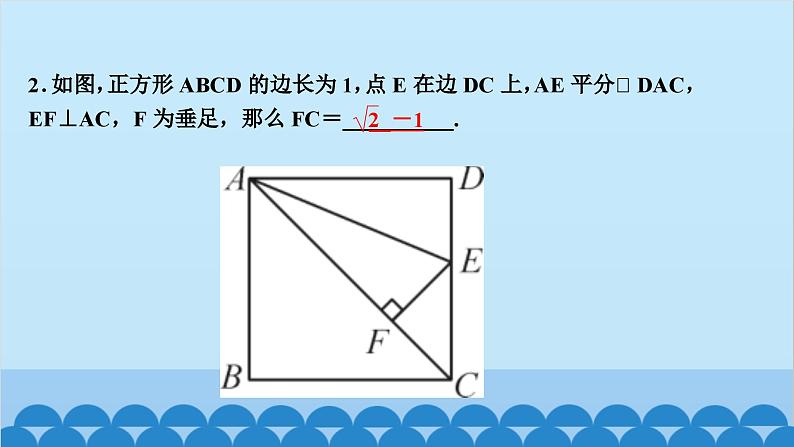
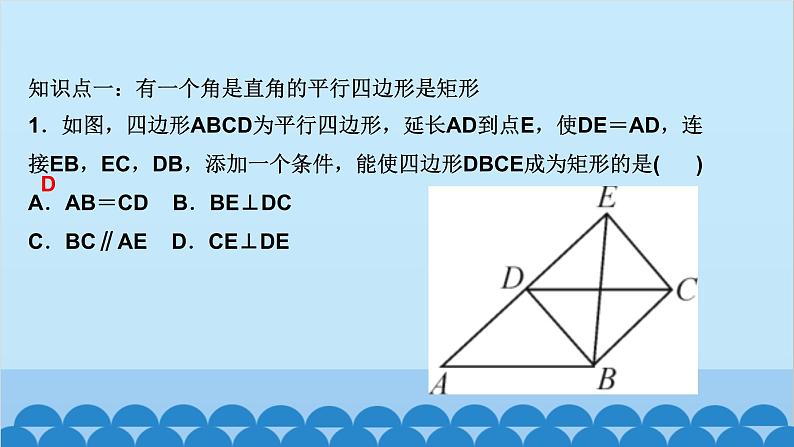
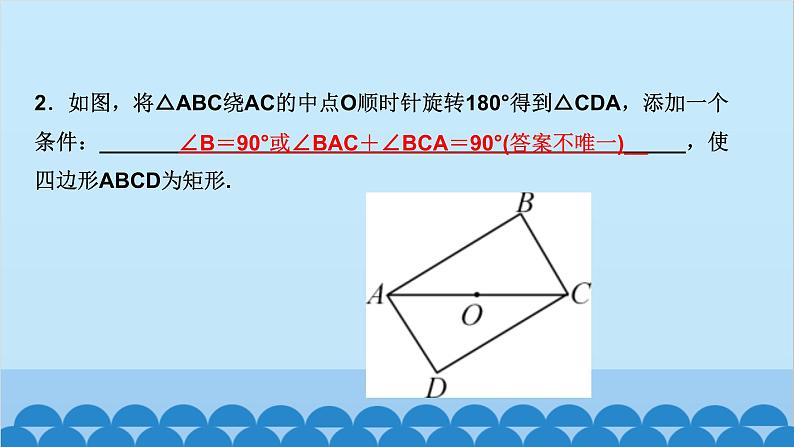
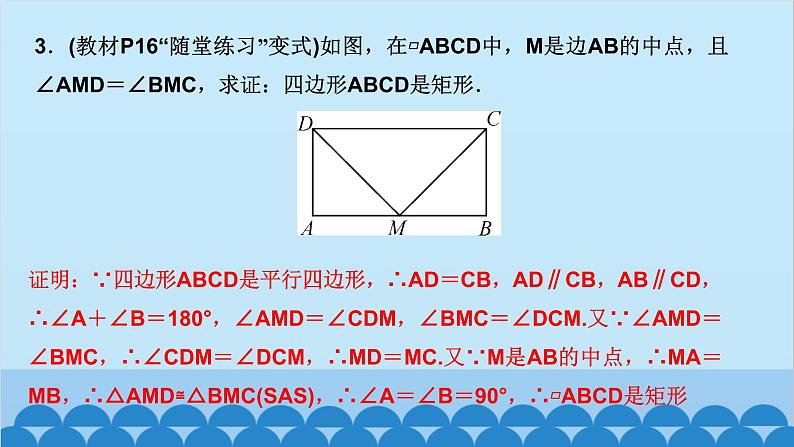
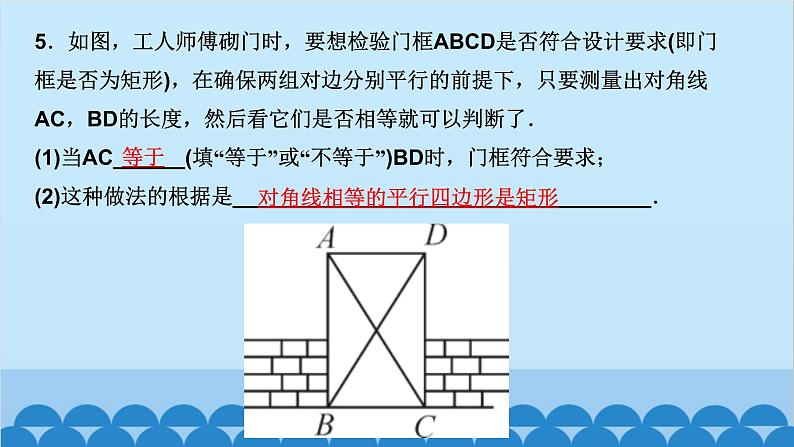
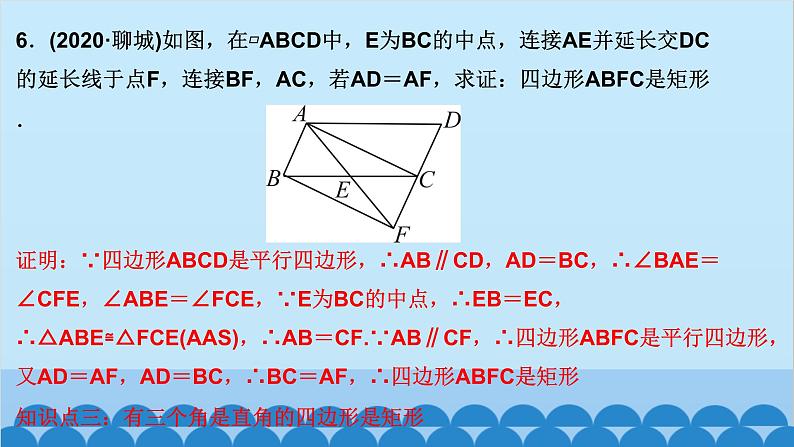
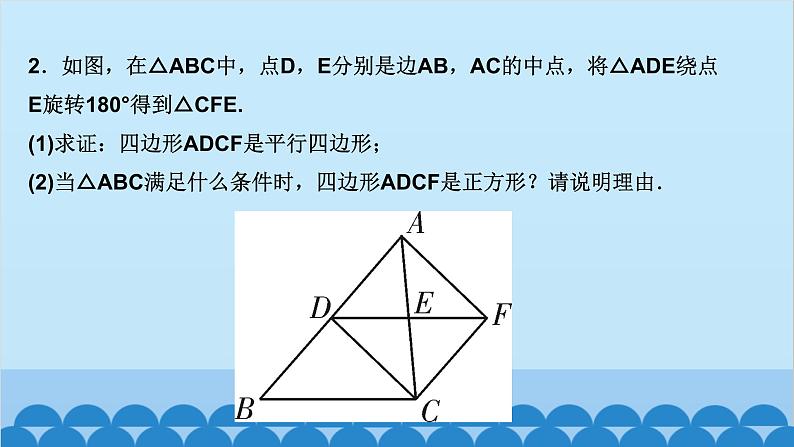
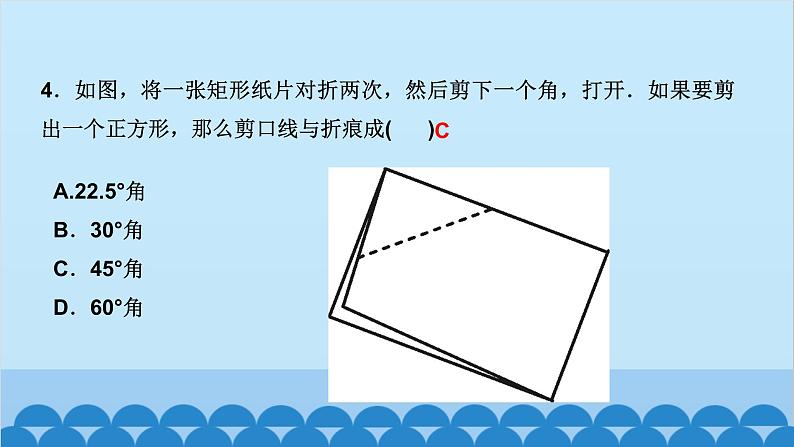
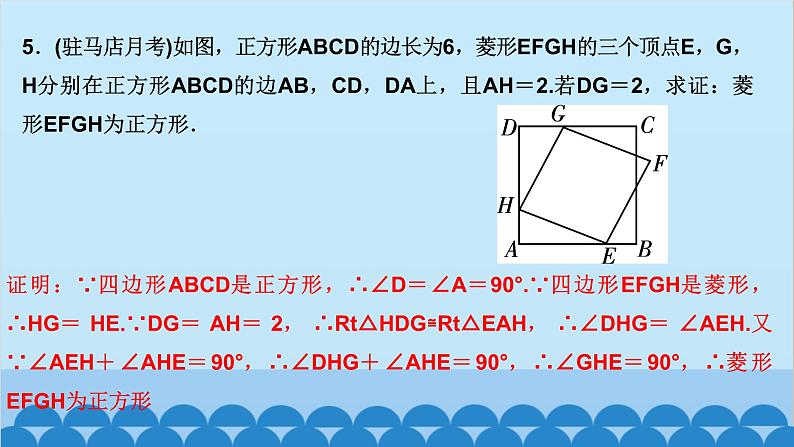
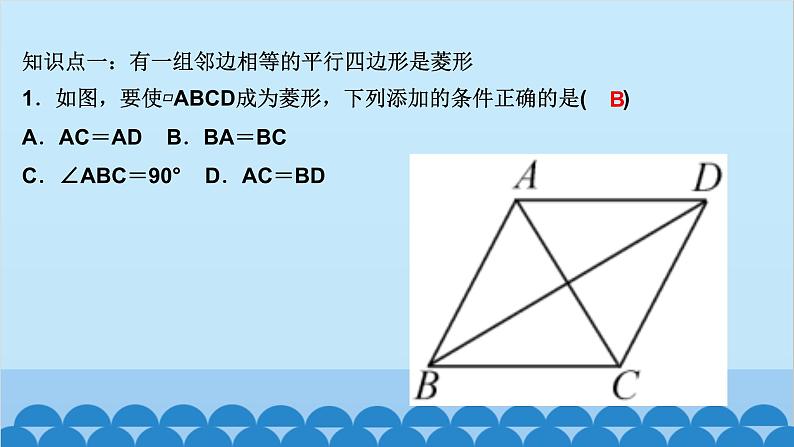
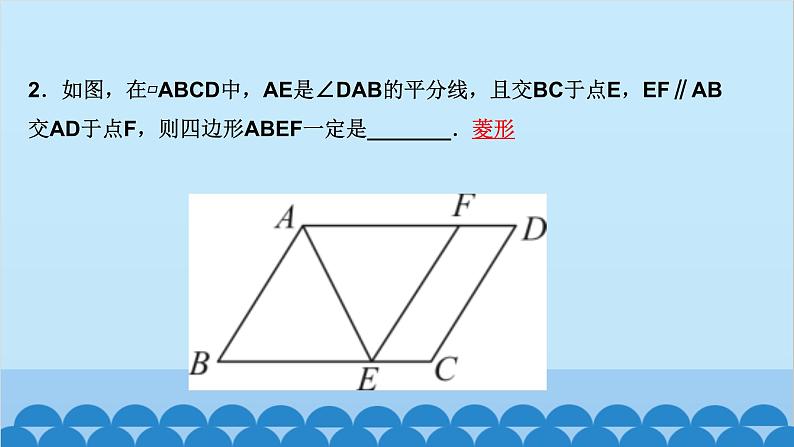
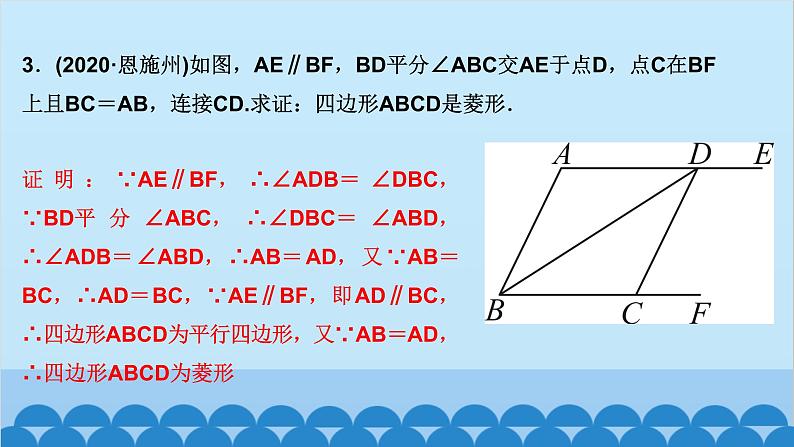
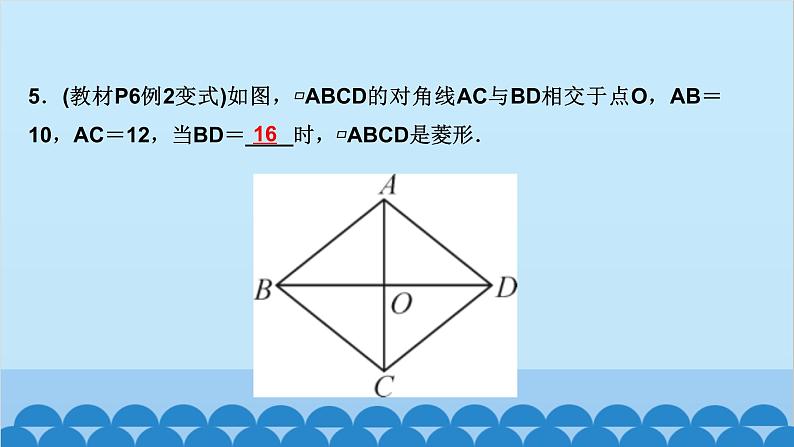
北师版1.2 矩形的性质与判定第一章 特殊平行四边形第2课时 矩形的判定知识点一:有一个角是直角的平行四边形是矩形1.如图,四边形ABCD为平行四边形,延长AD到点E,使DE=AD,连接EB,EC,DB,添加一个条件,能使四边形DBCE成为矩形的是( )A.AB=CD B.BE⊥DCC.BC∥AE D.CE⊥DED2.如图,将△ABC绕AC的中点O顺时针旋转180°得到△CDA,添加一个条件:_________________________________________________,使四边形ABCD为矩形.∠B=90°或∠BAC+∠BCA=90°(答案不唯一)__3.(教材P16“随堂练习”变式)如图,在▱ABCD中,M是边AB的中点,且∠AMD=∠BMC,求证:四边形ABCD是矩形.证明:∵四边形ABCD是平行四边形,∴AD=CB,AD∥CB,AB∥CD,∴∠A+∠B=180°,∠AMD=∠CDM,∠BMC=∠DCM.又∵∠AMD=∠BMC,∴∠CDM=∠DCM,∴MD=MC.又∵M是AB的中点,∴MA=MB,∴△AMD≌△BMC(SAS),∴∠A=∠B=90°,∴▱ABCD是矩形A 5.如图,工人师傅砌门时,要想检验门框ABCD是否符合设计要求(即门框是否为矩形),在确保两组对边分别平行的前提下,只要测量出对角线AC,BD的长度,然后看它们是否相等就可以判断了.(1)当AC______(填“等于”或“不等于”)BD时,门框符合要求;(2)这种做法的根据是___________________________________.等于对角线相等的平行四边形是矩形6.(2020·聊城)如图,在▱ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC,若AD=AF,求证:四边形ABFC是矩形.证明:∵四边形ABCD是平行四边形,∴AB∥CD,AD=BC,∴∠BAE=∠CFE,∠ABE=∠FCE,∵E为BC的中点,∴EB=EC,∴△ABE≌△FCE(AAS),∴AB=CF.∵AB∥CF,∴四边形ABFC是平行四边形,又AD=AF,AD=BC,∴BC=AF,∴四边形ABFC是矩形知识点三:有三个角是直角的四边形是矩形7.在数学活动课中,老师要求判断一个四边形门框是否为矩形,下面某合作小组的四位同学拟定的方案中,正确的是( )A.测量对角线是否互相平分B.测量两组对边是否相等C.测量一组对角是否为直角D.测量四个角是否都为直角D8.(怀化中考)如图,在▱ABCD中,AE⊥BC,CF⊥AD,E,F分别为垂足.(1)求证:△ABE≌△CDF;(2)求证:四边形AECF是矩形.9.如图,顺次连接四边形ABCD各边的中点,得到四边形EFGH,在下列条件中,能使四边形EFGH为矩形的是( )A.AB=CD B.AC=BDC.AC⊥BD D.AD∥BCC10.如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点(且点P不与点B,C重合),PE⊥AB于点E,PF⊥AC于点F,则EF的最小值为( )A.4 B.4.8 C.5.2 D.6B12.如图,在矩形ABCD中,AE=AF,过点E作EH⊥EF交DC于点H,过F作FG⊥EF交BC于点G,连接GH,当AD,AB满足_________(关系)时,四边形EFGH为矩形.AB=AD13.(2020·遂宁)如图,在△ABC中,AB=AC,点D,E分别是线段BC,AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.(1)求证:△BDE≌△FAE;(2)求证:四边形ADCF为矩形.证明:(1)∵AF∥BC,∴∠AFE=∠DBE,∵E是线段AD的中点,∴AE=DE,∵∠AEF=∠DEB,∴△BDE≌△FAE(AAS) (2)∵△BDE≌△FAE,∴AF=BD,∵D是线段BC的中点,∴BD=CD,∴AF=CD,∵AF∥CD,∴四边形ADCF是平行四边形,∵AB=AC,∴AD⊥BC,∴∠ADC=90°,∴四边形ADCF为矩形 14.(达州中考)如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB,外角∠ACD的平分线于点E,F.(1)若CE=8,CF=6,求OC的长;(2)连接AE,AF.问:当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.15.(青岛中考)如图,在▱ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接CG.(1)求证:△ABE≌△CDF;(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.






