广东省河源市紫金县2024-2025学年八年级上学期期中数学试卷

这是一份广东省河源市紫金县2024-2025学年八年级上学期期中数学试卷，共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（3分）下列各数中，为无理数的是（ ）
A．B．2.5C．0D．π
2．（3分）若二次根式在实数范围内有意义，则x的取值范围是（ ）
A．x＞2024B．x≥2024C．x＜2024D．x≤2024
3．（3分）下列二次根式化简后，与不是同类二次根式的是（ ）
A．B．C．D．
4．（3分）以下列各组数为边长，不能构成直角三角形的是（ ）
A．5，7，10B．3，4，5C．5，12，13D．
5．（3分）下列函数中，是一次函数的是（ ）
①y＝3x；②y＝x2+2；③y＝2x+1；④．
A．②④B．②③C．①③D．①②
6．（3分）在平面直角坐标系中，点P（﹣1，m2+1）位于（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
7．（3分）已知，则m的小数部分是（ ）
A．B．C．D．4
8．（3分）如图，正方体的棱长为2cm，点B为一条棱的中点．蚂蚁在正方体表面爬行，从点A爬到点B的最短路程是（ ）
A．cmB．4cmC．cmD．5cm
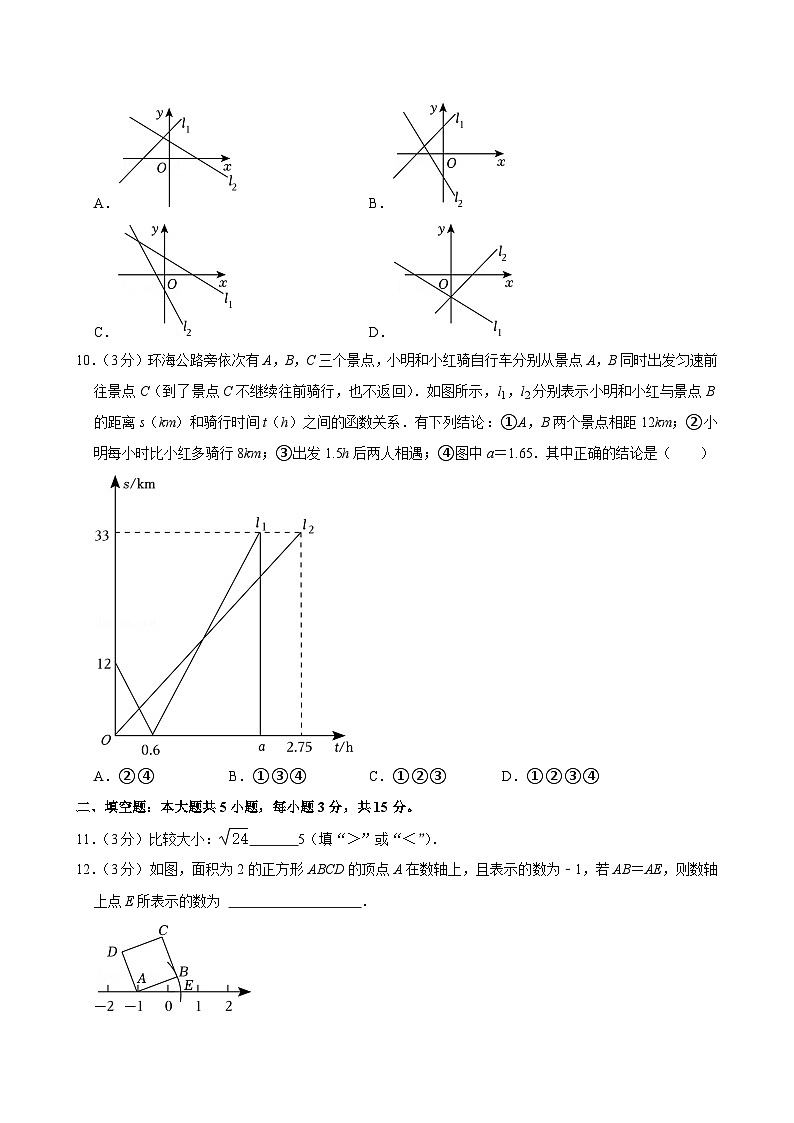
9．（3分）已知直线l1：y＝﹣kx+b与直线l2：y＝3kx﹣b在同一平面直角坐标系中的大致图象可能是（ ）
A．B．
C．D．
10．（3分）环海公路旁依次有A，B，C三个景点，小明和小红骑自行车分别从景点A，B同时出发匀速前往景点C（到了景点C不继续往前骑行，也不返回）．如图所示，l1，l2分别表示小明和小红与景点B的距离s（km）和骑行时间t（h）之间的函数关系．有下列结论：①A，B两个景点相距12km；②小明每小时比小红多骑行8km；③出发1.5h后两人相遇；④图中a＝1.65．其中正确的结论是（ ）
A．②④B．①③④C．①②③D．①②③④
二、填空题：本大题共5小题，每小题3分，共15分。
11．（3分）比较大小： 5（填“＞”或“＜”）．
12．（3分）如图，面积为2的正方形ABCD的顶点A在数轴上，且表示的数为﹣1，若AB＝AE，则数轴上点E所表示的数为 ．
13．（3分）将直线y＝5x+1向上平移6个单位长度后，得到的新直线的解析式是 ．
14．（3分）已知点P1（a﹣1，﹣5）和P2（﹣2，b﹣1）关于y轴对称，则（a+b）2024的值为 ．
15．（3分）在平面直角坐标系中，若点M（1，8）与点N（m，8）之间的距离是5，则m的值是 ．
三、解答题（一）：本大题共3小题，每小题7分，共21分。
16．（7分）计算：．
17．（7分）如图是小明所在学校的平面示意图，每个小正方形的边长均为1个单位长度，已知实验楼的位置是（﹣4，2），行政楼的位置是（3，﹣3）．
（1）根据题意，画出相应的平面直角坐标系；
（2）分别用坐标表示出餐厅、艺术楼的位置；
（3）若学校宿舍楼的位置是（﹣5，4），音乐楼的位置是（﹣4，﹣4），在图中标出它们的位置．
18．（7分）小明作为蓝信封行动的通信志愿者，有一次制作了一张面积为81cm2的正方形明信片想寄给对接的乡村小朋友．已知信封的长、宽之比为5：3，面积为150cm2．
（1）求长方形信封的长和宽；
（2）判断小明能否将这张明信片不折叠就放入此信封，并说明理由．
四、解答题（二）：本大题共3小题，每小题9分，共27分。
19．（9分）如图，6×6网格中每个小正方形的边长都为1，△ABC的顶点均在网格的格点上．
（1）AB＝ ，BC＝ ，AC＝ ；
（2）△ABC是直角三角形吗？请作出判断并说明理由．
20．（9分）已知2a+1的立方根是﹣5，a+2b的算术平方根是3，c是的整数部分．
（1）求a，b，c的值；
（2）求a+2b+c的平方根．
21．（9分）小英在家里整理内务时发现：把一些相同规格的塑料凳子整齐地叠放在水平地面上，这摞塑料凳子的高度随着凳子的数量变化有一定的关系．于是小英对凳子的高度进行测量，具体变化的情况如下表所示：
（1）上述两个变量之间的关系中，哪个是自变量？哪个是因变量？
（2）用h（cm）表示这摞凳子的高度，x（个）表示这摞凳子的数量，请写出h与x之间的函数关系式；
（3）当这摞凳子的高度为105cm时，求这摞凳子的数量．
五、解答题（三）：本大题共2小题，第22题13分，第23题14分，共27分。
22．（13分）甲骑电动车，乙骑自行车从深圳湾公园门口出发沿同一路线匀速游玩，设乙行驶的时间为x（h），甲、乙两人距出发点的路程S甲、S乙关于x的函数图象如图①所示，甲、乙两人之间的路程差y关于x的函数图象如图②所示，请你解决以下问题：
（1）甲的速度是 km/h，乙的速度是 km/h；
（2）对比图①、图②可知：a＝ ，b＝ ；
（3）乙出发多少时间，甲、乙两人路程差为7.5km？
23．（14分）【背景介绍】勾股定理是几何学中的明珠，充满着魅力．如图1是著名的赵爽弦图，由四个全等的直角三角形拼成，用它可以证明勾股定理，思路是大正方形的面积有两种求法，一种是等于c2，另一种是等于四个直角三角形与一个小正方形的面积之和，即ab×4+（b﹣a）2，从而得到等式c2＝ab×4+（b﹣a）2，化简便得出结论a2+b2＝c2．这里用两种求法来表示同一个量从而得到等式或方程的方法，我们称之为“双求法”．
【方法运用】千百年来，人们对勾股定理的证明趋之若鹜．某数学爱好者构造发现了以下证法：把两个全等的直角三角形ABC和直角三角形DEA按如图2所示放置，其三边长分别为a，b，c，∠BAC＝∠DEA＝90°，显然BC⊥AD．
（1）请用a，b，c分别表示出四边形ABDC，梯形AEDC，△EBD的面积，再利用这三个图形面积之间的关系，证明勾股定理a2+b2＝c2；
【方法迁移】
（2）如图3，小正方形边长为1，连接小正方形的三个顶点，可得到△ABC，则AB边上的高为 ；
（3）如图4，在△ABC中，AD是BC边上的高，AB＝4，AC＝5，BC＝6，设BD＝x，求x的值．
2024-2025学年广东省河源市紫金县八年级（上）期中数学试卷
参考答案与试题解析
一、选择题：本大题共10小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的。
1．（3分）下列各数中，为无理数的是（ ）
A．B．2.5C．0D．π
【答案】D
【分析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．
【解答】解：A、是分数，不是无理数，不符合题意；
B、2.5是小数，不是无理数，不符合题意；
C、0是整数，不是无理数，不符合题意；
D、π是无理数，符合题意，
故选：D．
【点评】此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽得到的数；以及像0.1010010001…，等有这样规律的数．
2．（3分）若二次根式在实数范围内有意义，则x的取值范围是（ ）
A．x＞2024B．x≥2024C．x＜2024D．x≤2024
【答案】B
【分析】根据二次根式的被开方数不小于零的条件和分母不为零的条件进行解题即可．
【解答】解：由题可知，
x﹣2024≥0且x≠0，
解得x≥2024．
故选：B．
【点评】本题考查二次根式有意义的条件、分式有意义的条件，熟练掌握相关的知识点是解题的关键．
3．（3分）下列二次根式化简后，与不是同类二次根式的是（ ）
A．B．C．D．
【答案】B
【分析】先根据二次根式的性质进行化简，再根据同类二次根式的定义进行解题即可．
【解答】解：A、＝与是同类二次根式，故A不正确；
B、＝2与不是同类二次根式，故B正确；
C、＝4与是同类二次根式，故C不正确；
D、＝2是同类二次根式，故D不正确；
故选：B．
【点评】本题考查同类二次根式、二次根式的性质与化简，熟练掌握相关的知识点是解题的关键．
4．（3分）以下列各组数为边长，不能构成直角三角形的是（ ）
A．5，7，10B．3，4，5C．5，12，13D．
【答案】A
【分析】由勾股定理的逆定理，只要验证两小边的平方和等于最长边的平方即可．
【解答】解：A、52+72≠102，故不是直角三角形，故此选项符合题意；
B、32+42＝52，故是直角三角形，故此选项不符合题意；
C、52+122＝132，故是直角三角形，故此选项不符合题意；
D、12+（）2＝22，故是直角三角形，故此选项不符合题意
故选：A．
【点评】本题考查了勾股定理的逆定理，正确验证两小边的平方和等于最长边的平方是解题的关键．
5．（3分）下列函数中，是一次函数的是（ ）
①y＝3x；②y＝x2+2；③y＝2x+1；④．
A．②④B．②③C．①③D．①②
【答案】C
【分析】根据是一次函数的定义逐一判断即可．
【解答】解：①y＝3x是一次函数；
②y＝x2+2是二次函数；
③y＝2x+1是一次函数；
④y＝是反比例函数，
所以①③是一次函数．
故选：C．
【点评】本题主要考查一次函数，熟练掌握是一次函数的定义是解题的关键．
6．（3分）在平面直角坐标系中，点P（﹣1，m2+1）位于（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【答案】B
【分析】依据m2+1＞0，即可得出点P（﹣1，m2+1）在第二象限．
【解答】解：∵m2+1＞0，
∴点P（﹣1，m2+1）在第二象限．
故选：B．
【点评】本题考查了各象限内点的坐标的符号特征和平方的非负性，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．
7．（3分）已知，则m的小数部分是（ ）
A．B．C．D．4
【答案】C
【分析】根据算术平方根的定义得到＝3，再根据算术平方根的定义估算无理数的大小，进而得到3+的大小即可．
【解答】解：m＝+＝3+，
∵1＜＜2，
∴4＜3+＜5，
∴3+的整数部分是4，小数部分为3+﹣4＝﹣1．
故选：C．
【点评】本题考查估算无理数的大小，掌握算术平方根的定义是正确解答的关键．
8．（3分）如图，正方体的棱长为2cm，点B为一条棱的中点．蚂蚁在正方体表面爬行，从点A爬到点B的最短路程是（ ）
A．cmB．4cmC．cmD．5cm
【答案】C
【分析】正方体侧面展开为长方形，确定蚂蚁爬行的起点和终点，根据两点之间线段最短，根据勾股定理可求出最短路径长，
【解答】解：如图，
它运动的最短路程AB＝＝（cm）．
故选：C．
【点评】本题考查平面展开最短路径问题，关键是知道两点之间线段最短，找到起点终点，根据勾股定理求出答案．
9．（3分）已知直线l1：y＝﹣kx+b与直线l2：y＝3kx﹣b在同一平面直角坐标系中的大致图象可能是（ ）
A．B．
C．D．
【答案】B
【分析】根据两个一次函数的图象逐一分析系数符号即可解决．
【解答】解：A、直线l1：y＝﹣kx+b中k＜0，b＞0，l2：y＝3kx﹣b中k＞0，b＜0，b的取值相矛盾，故本选项不符合题意；
B、直线l1：y＝﹣kx+b中k＜0，b＞0，l2：y＝3kx﹣b中k＜0，b＞0，k、b的取值一致，故本选项符合题意；
C、直线l1：y＝﹣kx+b中k＞0，b＞0，l2：y＝3kx﹣b中k＜0，b＞0，k的取值相矛盾，故本选项不符合题意；
D、直线l1：y＝﹣kx+b中k＞0，b＜0，l2：y＝3kx﹣b中k＞0，b＞0，b的取值相矛盾，故本选项不符合题意．
故选：B．
【点评】本题考查了一次函数的图象与性质，掌握一次函数的图象与性质，数形结合是本题的关键．
10．（3分）环海公路旁依次有A，B，C三个景点，小明和小红骑自行车分别从景点A，B同时出发匀速前往景点C（到了景点C不继续往前骑行，也不返回）．如图所示，l1，l2分别表示小明和小红与景点B的距离s（km）和骑行时间t（h）之间的函数关系．有下列结论：①A，B两个景点相距12km；②小明每小时比小红多骑行8km；③出发1.5h后两人相遇；④图中a＝1.65．其中正确的结论是（ ）
A．②④B．①③④C．①②③D．①②③④
【答案】C
【分析】由图象直接得到AB间的距离，即可判断选项①；分别求得小明、小红的速度，然后相减即可得解选项②；设出发m h后两人相遇，依题意得到20（m﹣0.6）＝12m，解答即可判断③；把两段时间相加即可得解．
【解答】解：由图象可得，
A，B两村相距12km，
故①正确，符合题意；
小明的速度为：12÷0.6＝20（km/h），小红的速度为：33÷2.75＝12（km/h），
则小明每小时比小红多骑行20﹣12＝8（km/h），
故②正确，符合题意；
设出发m h后两人相遇，
则20（m﹣0.6）＝12m，
解得m＝1.5，
即出发1.5h后两人相遇，
故③正确，符合题意；
a＝0.6+33÷20＝2.25，
故④错误，不符合题意，
∴正确的结论是①②③；
故选：C．
【点评】本题考查一次函数的应用，解答本题的关键是明确题意，利用数形结合的思想解答．
二、填空题：本大题共5小题，每小题3分，共15分。
11．（3分）比较大小： ＜ 5（填“＞”或“＜”）．
【答案】见试题解答内容
【分析】先估算出的范围，即可得出答案．
【解答】解：∵5＝，
∴4＜＜5，
∴＜5，
故答案为：＜．
【点评】本题考查了实数的大小比较和算术平方根，能估算出的范围是解此题的关键．
12．（3分）如图，面积为2的正方形ABCD的顶点A在数轴上，且表示的数为﹣1，若AB＝AE，则数轴上点E所表示的数为 ．
【答案】．
【分析】先求出AB的长，再求E的坐标．
【解答】解：∵正方形ABCD的面积为2，
∴AB＝．
∴AE＝AB＝．
∵A的坐标为﹣1，E在点A的右侧，
∴E的坐标为．
故答案为：．
【点评】本题考查实数与数轴．解题关键是求出AB的长为．
13．（3分）将直线y＝5x+1向上平移6个单位长度后，得到的新直线的解析式是 y＝5x+7 ．
【答案】y＝5x+7．
【分析】根据函数图象的平移规则“上加下减”，即可得出直线平移后的解析式．
【解答】解：将直线y＝5x+1向上平移6个单位长度后，得到的新直线的解析式是y＝5x+1+6，即y＝5x+7．
故答案为：y＝5x+7．
【点评】本题考查了一次函数图象与几何变换，解题的关键是熟记函数平移的规则“上加下减”．
14．（3分）已知点P1（a﹣1，﹣5）和P2（﹣2，b﹣1）关于y轴对称，则（a+b）2024的值为 1 ．
【答案】1．
【分析】关于y轴对称的点的横坐标互为相反数，纵坐标相等，由此可得a﹣1＝﹣（﹣2）＝2，b﹣1＝﹣5，可得a＝3，b＝﹣4，进而可得答案．
【解答】解：∵点P1（a﹣1，﹣5）和P2（﹣2，b﹣1）关于y轴对称，
∴a﹣1＝﹣（﹣2）＝2，b﹣1＝﹣5，
解得a＝3，b＝﹣4，
∴（a+b）2024＝（﹣1）2024＝1．
故答案为：1．
【点评】本题考查关于x轴、y轴对称的点的坐标，熟练掌握关于y轴对称的点的坐标特征是解答本题的关键．
15．（3分）在平面直角坐标系中，若点M（1，8）与点N（m，8）之间的距离是5，则m的值是 6或﹣4 ．
【答案】6或﹣4．
【分析】根据M、N两点的纵坐标相等可以判断MN平行于x轴，且MN之间距离是5，可以得出N点的坐标，进而求出m的值．
【解答】解：∵点M（1，8）与点N（m，8），
∴MN∥x轴，
∵MN＝5，
∴1+5＝6，1﹣5＝﹣4，
∴N（﹣4，8）或（6，8），
∴m的值为6或﹣4．
故答案为：6或﹣4．
【点评】题目考查了平面直角坐标系中利用两点之间的距离求点的坐标，题目相对较为简单，但是本题有两种情况，不要遗漏m的解．
三、解答题（一）：本大题共3小题，每小题7分，共21分。
16．（7分）计算：．
【答案】．
【分析】先计算算术平方根、绝对值、立方根、再计算加减法即可．
【解答】解：
＝，
＝．
【点评】本题考查了实数的混合运算，掌握相关运算法则是解题关键．
17．（7分）如图是小明所在学校的平面示意图，每个小正方形的边长均为1个单位长度，已知实验楼的位置是（﹣4，2），行政楼的位置是（3，﹣3）．
（1）根据题意，画出相应的平面直角坐标系；
（2）分别用坐标表示出餐厅、艺术楼的位置；
（3）若学校宿舍楼的位置是（﹣5，4），音乐楼的位置是（﹣4，﹣4），在图中标出它们的位置．
【答案】（1）作图见解析过程；
（2）餐厅（4，4），艺术楼（﹣2，﹣1）；
（3）作图见解析过程．
【分析】（1）根据实验楼和行政楼的坐标，确定原点，再画出平面直角坐标系即可；
（2）根据（1）中建立的平面直角坐标系，即可解答；
（3）根据坐标，再图中标出即可．
【解答】解：（1）如图1所示：
（2）由图可知：餐厅（4，4），艺术楼（﹣2，﹣1）；
（3）宿舍楼和音乐楼的位置如图所示．
【点评】此题主要考查了坐标确定位置，正确得出原点的位置是解题关键．
18．（7分）小明作为蓝信封行动的通信志愿者，有一次制作了一张面积为81cm2的正方形明信片想寄给对接的乡村小朋友．已知信封的长、宽之比为5：3，面积为150cm2．
（1）求长方形信封的长和宽；
（2）判断小明能否将这张明信片不折叠就放入此信封，并说明理由．
【答案】（1）cm，cm；
（2）小明能将明信片不折叠就放入此信封，理由见解答过程．
【分析】（1）依题意设信封的长是5x cm，宽是3x cm，根据信封的面积是150cm2列出方程，解出x即可得出信封的长和宽；
（2）先求出正方形明信片的边长是9cm，根据＞9即可得出答案．
【解答】解：（1）∵信封的长、宽之比为5：3，
∴设信封的长是5x cm，宽是3x cm，
又∵信封的面积是150cm2，
∴5x•3x＝150，
解得：x＝，或x＝（不合题意，舍去），
∴5x＝cm，3x＝cm，
答：信封的长是cm，宽是cm．
（2）小明能将明信片不折叠就放入此信封，理由如下：
∵正方形明信片的面积是81cm2，
∴正方形明信片的边长是9cm，
∵，
∴小明能将明信片不折叠就放入此信封．
【点评】此题主要考查了正方形的性质，矩形的性质，比的应用，熟练掌握正方形的性质，矩形的性质是解决问题的关键．
四、解答题（二）：本大题共3小题，每小题9分，共27分。
19．（9分）如图，6×6网格中每个小正方形的边长都为1，△ABC的顶点均在网格的格点上．
（1）AB＝ ，BC＝ ，AC＝ 5 ；
（2）△ABC是直角三角形吗？请作出判断并说明理由．
【答案】（1），，5；
（2）直角三角形．
【分析】（1）根据勾股定理计算即可求解．
（2）直接把三边长度分别平方，可以发现AB2+BC2＝AC2即可判定三角形的形状；
【解答】解：（1）由题可知，AB＝＝；
AC＝＝5
BC＝＝，
故答案为：，，5；
（2）直角三角形，
∵AB2＝5，BC2＝20，AC2＝25；
∴AB2+BC2＝AC2；
∴△ABC为直角三角形．
【点评】本题考查的是勾股定理的逆定理及勾股定理，熟知如果三角形的三边长a，b，c满足a2+b2＝c2，那么这个三角形就是直角三角形是解题的关键．
20．（9分）已知2a+1的立方根是﹣5，a+2b的算术平方根是3，c是的整数部分．
（1）求a，b，c的值；
（2）求a+2b+c的平方根．
【答案】（1）a＝﹣63，b＝36，c＝3；
（2）±2．
【分析】（1）根据立方根、算术平方根的定义可确定a、b的值，由算术平方根的定义可估算无理数的大小，进而确定c的值；
（2）代入求出a+2b+c的值，再求其平方根．
【解答】解：（1）∵2a+1的立方根是﹣5，
∴2a+1＝（﹣5）3，
解得a＝﹣63，
又∵a+2b的算术平方根是3，
∴a+2b＝9，而a＝﹣63，
∴b＝36，
∵3＜＜4，而c是的整数部分，
∴c＝3，
答：a＝﹣63，b＝36，c＝3；
（2）∵a＝﹣63，b＝36，c＝3，
∴a+2b+c＝﹣63+72+3＝12，
∴a+5b+c的平方根＝±2．
【点评】本题考查立方根、平方根、算术平方根以及估算无理数的大小，理解平方根、算术平方根、立方根的定义是掌正确解答的关键．
21．（9分）小英在家里整理内务时发现：把一些相同规格的塑料凳子整齐地叠放在水平地面上，这摞塑料凳子的高度随着凳子的数量变化有一定的关系．于是小英对凳子的高度进行测量，具体变化的情况如下表所示：
（1）上述两个变量之间的关系中，哪个是自变量？哪个是因变量？
（2）用h（cm）表示这摞凳子的高度，x（个）表示这摞凳子的数量，请写出h与x之间的函数关系式；
（3）当这摞凳子的高度为105cm时，求这摞凳子的数量．
【答案】（1）凳子的数量是自变量，高度是因变量；（2）h＝5x+45；（3）12个．
【分析】（1）根据表格中列举的变量即可求解；
（2）根据表格中数据变化规律求解即可；
（3）根据（2）中的函数关系式，把h＝105cm代入求解即可．
【解答】解：（1）通过表格所列举的变量可知，凳子的数量是自变量，高度是因变量；
（2）由表格中两个变量的变化关系可得，
h＝50+5（x﹣1）＝5x+45，
即h＝5x+45；
（3）当h＝105cm时，即5x+45＝105，
解得x＝12，
答：当这摞凳子的高度为105cm时，凳子的数量为12个．
【点评】本题考查了函数的表示方法，常量与变量、函数关系式，掌握相应的定义是关键．
五、解答题（三）：本大题共2小题，第22题13分，第23题14分，共27分。
22．（13分）甲骑电动车，乙骑自行车从深圳湾公园门口出发沿同一路线匀速游玩，设乙行驶的时间为x（h），甲、乙两人距出发点的路程S甲、S乙关于x的函数图象如图①所示，甲、乙两人之间的路程差y关于x的函数图象如图②所示，请你解决以下问题：
（1）甲的速度是 25 km/h，乙的速度是 10 km/h；
（2）对比图①、图②可知：a＝ 10 ，b＝ 1.5 ；
（3）乙出发多少时间，甲、乙两人路程差为7.5km？
【答案】（1）25，10；
（2）10；1.5；
（3）h或h．
【分析】（1）根据题意和函数图象中的数据可以求得甲乙的速度；
（2）根据题意和图象中的数据，可以分别得到a、b的值；
（3）由图象可知甲乙相距7.5km有两种情况，然后分别计算两种情况下乙出发的时间即可解答本题．
【解答】解：（1）由图可得，
甲的速度为：25÷（1.5﹣0.5）＝25÷1＝25（km/h），乙的速度为：25÷2.5＝10（km/h），
故答案为：25，10；
（2）由图可得，
a＝25×（1.5﹣0.5）﹣10×1.5＝10，
b＝1.5，
故答案为：10；1.5；
（3）由题意可得，
前0.5h，乙行驶的路程为：10×0.5＝5＜7.5，
则甲、乙两人路程差为7.5km是在甲乙相遇之后，
设乙出发xh时，甲、乙两人路程差为7.5km，
25（x﹣0.5）﹣10x＝7.5，
解得，x＝，
25﹣10x＝7.5，得x＝；
即乙出发或时，甲、乙两人路程差为7.5km．
【点评】本题考查一次函数的应用，解答本题的关键是明确题意，利用一次函数的性质和数形结合的思想解答．
23．（14分）【背景介绍】勾股定理是几何学中的明珠，充满着魅力．如图1是著名的赵爽弦图，由四个全等的直角三角形拼成，用它可以证明勾股定理，思路是大正方形的面积有两种求法，一种是等于c2，另一种是等于四个直角三角形与一个小正方形的面积之和，即ab×4+（b﹣a）2，从而得到等式c2＝ab×4+（b﹣a）2，化简便得出结论a2+b2＝c2．这里用两种求法来表示同一个量从而得到等式或方程的方法，我们称之为“双求法”．
【方法运用】千百年来，人们对勾股定理的证明趋之若鹜．某数学爱好者构造发现了以下证法：把两个全等的直角三角形ABC和直角三角形DEA按如图2所示放置，其三边长分别为a，b，c，∠BAC＝∠DEA＝90°，显然BC⊥AD．
（1）请用a，b，c分别表示出四边形ABDC，梯形AEDC，△EBD的面积，再利用这三个图形面积之间的关系，证明勾股定理a2+b2＝c2；
【方法迁移】
（2）如图3，小正方形边长为1，连接小正方形的三个顶点，可得到△ABC，则AB边上的高为 ；
（3）如图4，在△ABC中，AD是BC边上的高，AB＝4，AC＝5，BC＝6，设BD＝x，求x的值．
【答案】（1）证明见解答过程；
（2）；
（3）．
【分析】（1）表示出三个图形的面积进行加减计算可证a2+b2＝c2；
（2）计算出△ABC的面积，再根据三角形的面积公式即可求得AB边上的高；
（3）运用勾股定理在Rt△ABD和Rt△ADC中求出AD2，列出方程求解即可．
【解答】（1）证明：∵S四边形ABCD＝c2，S梯形AEDC＝（b+a）b，，S四边形ABCD＝S梯形AEDC+S△BED，
∴，
∴，
∴a2+b2＝c2；
（2）解：设AB边上的高为h，则：
，，
∴，
∴，
即AB边上的高是，
故答案为：；
（3）解：在Rt△ABD中，由勾股定理得AD2＝AB2﹣BD2＝42﹣x2＝16﹣x2，
∵BD+CD＝BC＝6，
∴CD＝BC﹣BD＝6﹣x，
在Rt△ACD中，由勾股定理得AD2＝AC2﹣CD2＝52﹣（6﹣x）2＝﹣11+12x﹣x2，
∴16﹣x2＝﹣11+12x﹣x2，
∴．
【点评】此题主要考查了勾股定理的证明，三角形的面积，利用面积证明勾股定理是解答本题的关键．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2024/11/26 1:29:09；用户：18328501451；邮箱：18328501451；学号：43314264凳子的数量/个
1
2
3
4
5
…
高度/cm
50
55
60
65
70
…
凳子的数量/个
1
2
3
4
5
…
高度/cm
50
55
60
65
70
…