2025届广西钦州市灵山县高三(上)11月月考数学试卷(解析版)

这是一份2025届广西钦州市灵山县高三(上)11月月考数学试卷(解析版)，共13页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。

1. 若集合{}，，则（ ）
A. B.
C. D.
【答案】D
【解析】由题可得.
故选：D
2. 若直线与直线相互平行，则的值为（ ）
A. B. C. D.
【答案】C
【解析】因为直线与直线相互平行，
所以，即，解得或.
故选：C.
3. 已知为钝角，向量，若，则（ ）
A. B. C. D. 或
【答案】C
【解析】由，得，则，即，
由为钝角，得0，解得，所以.
故选：C
4. 已知向量满足，则的值为（ ）
A B. C. 8D. 5
【答案】B
【解析】由两边平方得，
由两边平方得，
所以.
故选：B
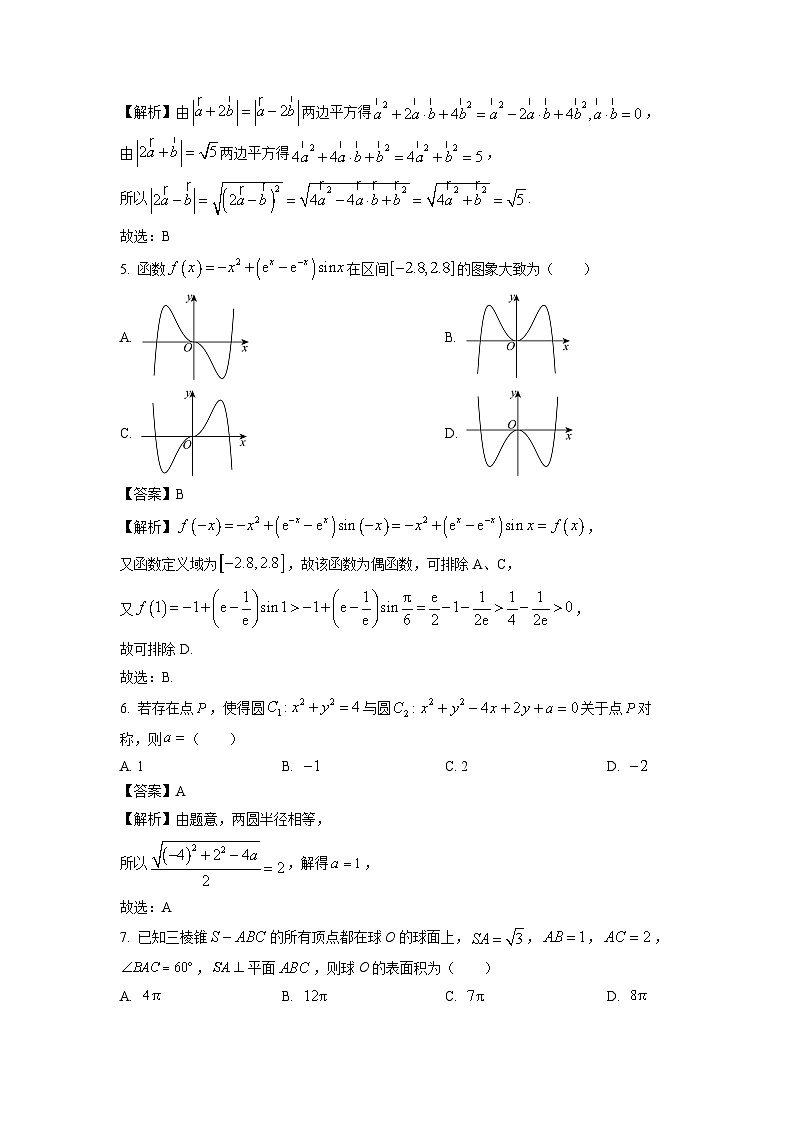
5. 函数在区间的图象大致为（ ）
A. B.
C. D.
【答案】B
【解析】，
又函数定义域为，故该函数为偶函数，可排除A、C，
又，
故可排除D.
故选：B.
6. 若存在点，使得圆与圆关于点对称，则（ ）
A. 1B. C. 2D.
【答案】A
【解析】由题意，两圆半径相等，
所以，解得，
故选：A
7. 已知三棱锥的所有顶点都在球O的球面上，，，，，平面，则球O的表面积为（ ）
A. B. C. D.
【答案】C
【解析】在三棱锥中，球心在棱的中垂面上，由平面，得平面，
则球心到平面的距离为，在中，由余弦定理得：
，
因此外接圆半径，球的半径，
所以球O表面积.
故选：C
8. 若函数在定义域上的值域为，则称为“函数”．已知函数是“函数”，则实数的取值范围是（ ）
A. B.
C. D.
【答案】C
【解析】由题意可知的定义域为，
又因为函数是“函数”，故其值域为；
而，则值域为；
当时，，
当时，，此时函数在上单调递增，则，
故由函数是“函数”可得，
解得，即实数的取值范围是，
故选：C
二、多选题
9. 已知函数的图像关于点中心对称，则（ ）
A. 在区间单调递减
B. 在区间有两个极值点
C. 直线是曲线的对称轴
D. 直线是曲线的切线
【答案】AD
【解析】由题意得：f2π3=sin4π3+φ=0，所以，，
即，
又，所以时，，故．
对A，当时，，由正弦函数图象知在上是单调递减；
对B，当时，，由正弦函数图象知只有1个极值点，由，解得，即为函数的唯一极值点；
对C，当时，，f(7π6)=0，直线不是对称轴；
对D，由y'=2cs2x+2π3=-1得：cs2x+2π3=-12，
解得或
从而得：或,
所以函数在点处的切线斜率为k=y'x=0=2cs2π3=-1，
切线方程为：y-32=-(x-0)即．
故选：AD．
10. 已知双曲线的左、右焦点分别为，，过作斜率为的直线与双曲线的右支交于，两点（在第一象限），，为线段的中点，为坐标原点，则（ ）
A. B. 双曲线的离心率为
C. 的面积为D. 直线的斜率为
【答案】ABD
【解析】如下图所示：
对于A选项，因为，所以，
由双曲线的定义可得，所以，，所以选项A正确，
对于B选项，设直线的斜率为，设直线的倾斜角为，则为锐角且，
由可得，
则，
在中，由余弦定理得，
即，
等式两边同时除以可得，
因为，解得，所以选项B正确，
对于C选项，因为，则为钝角，
所以，
，
所以选项C错误，
对于D选项，设Ax1,y1，Bx2,y2，
则，可得，
因为，则，
由，得，
所以，则，
则直线的斜率为，所以选项D正确，
故选：ABD．
11. 对于定义在上的函数，若是奇函数，是偶函数，且在上单调递减，则（ ）
A.
B.
C
D. 在上单调递减
【答案】BCD
【解析】若是奇函数，即它的图象关于原点对称，
把的图象向左平移1个单位，再向上平移一个单位得的图象，
因此的图象关于点对称，所以，，
是偶函数，即它的图象关于轴对称，的图象向右平移一个单位得的图象，
因此的图象关于直线对称，从而，，B正确；
所以，即，
，所以，A错；
，C正确；
在上递减，它关于直线对称，则在上递增，
又它的图象关于点对称，则在上递增，
再由它关于直线对称得它在上递减，D正确，
故选：BCD．
三、填空题
12. 若数列为首项为3，公比为2的等比数列，则_______．
【答案】189
【解析】由数列为首项为3，公比为2的等比数列，得.
13. 若，且，则__________.
【答案】
【解析】由，得.
因为，所以，则，则.
由，得，则，解得.
14. 袋中有2个白球，1个红球，这些球除颜色外完全相同.现从袋中往外取球，每次任取1个记下颜色后放回，直到红球出现2次时停止，设停止时共取了次球，则_______．
【答案】
【解析】由题意可知最后一次取到的是红球，前3次有1次取到红球，所以，填．
四、解答题
15. 记的内角A、B、C的对边分别为a，b，c，已知，
（1）求B；
（2）若的面积为，求c．
解：（1）由余弦定理有，对比已知，
可得，
因为，所以，
从而，
又因为，即，注意到，
所以.
（2）由（1）可得，，，
从而，，
而，
由正弦定理有，
从而，
由三角形面积公式可知，的面积可表示为
，
由已知的面积为，可得，
所以.
16. 已知函数．
（1）若，求函数的最小值；
（2）若函数在区间上是减函数，求实数a的取值范围．
解：（1）当时，，且，
令，即；
，，
所以在上单调递减，在上单调递增.
所以当时，函数取最小值为．
（2）因为函数在区间上是减函数，
所以在区间上恒成立．
即在上恒成立，
则在上恒成立，
令，，
显然在区间上单调递减，在区间上单调递增，
则， 所以，实数的取值范围为.
17. 如图，、、为圆锥三条母线，.
（1）证明:；
（2）若圆锥侧面积为为底面直径，，求二面角的大小
（1）证明：取中点，连接、，
因为，所以，
又因为面面，所以面，
因为面，所以.
（2）解：因为为直径，故为底面圆的圆心，故平面，而
故可建立如图所示的空间直角坐标系，
因为圆锥侧面积为为底面直径，，所以底面半径为1，母线长为3，
所以，
则可得，
故，
设为平面的法向量，则，
令，则，所以.
设为平面的法向量，
则，
令，则，所以.
则，
设二面角为，则为钝角，
所以二面角的大小为.
18. 水果分为一级果和二级果，共136箱，其中一级果102箱，二级果34箱．
（1）随机挑选两箱水果，求恰好一级果和二级果各一箱的概率；
（2）进行分层抽样，共抽8箱水果，求一级果和二级果各几箱；
（3）抽取若干箱水果，其中一级果共120个，单果质量平均数为303.45克，方差为603.46；二级果48个，单果质量平均数为240.41克，方差为648.21；求168个水果的方差和平均数，并预估果园中单果的质量．
解：（1）设A事件为恰好选到一级果和二级果各一箱，
样本空间的样本点的个数，
A事件的样本点的公式，
所以；
（2）因为一级果箱数：二级果箱数，
所以8箱水果中有一级果抽取箱，二级果抽取箱；
（3）设一级果平均质量为，方差为，二级果质量为，方差为，
总体样本平均质量为，方差为，
因为，，，，
所以克，
克．
预估平均质量为克．
19. 已知椭圆的离心率为12．左顶点为，下顶点为是线段的中点（O为原点），的面积为．
（1）求椭圆的方程．
（2）过点C的动直线与椭圆相交于两点．在轴上是否存在点，使得恒成立．若存在，求出点纵坐标的取值范围；若不存在，请说明理由．
解：（1）因为椭圆的离心率为，故，，其中为半焦距，
所以，故，
故，所以，，故椭圆方程为：.
（2）若过点的动直线的斜率存在，则可设该直线方程为：，
设，
由可得，
故且
而，
故
，
因为恒成立，故，解得.
若过点的动直线的斜率不存在，则或，
此时需，两者结合可得.
综上，存在，使得恒成立.