福州市时代华威中学2024—2025学年上学期期中考试八年级数学试卷(无答案)

展开

这是一份福州市时代华威中学2024—2025学年上学期期中考试八年级数学试卷(无答案)，共4页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
班级：座号：姓名：成绩：
一、选择题：本题共10小题，每小题4分，共40分。
1．下列图案是轴对称图形的是（）.
A．B．C．D．
2．在平面直角坐标系中，点P(-1,2)关于y轴对称的点是（）.
A．(-1,-2)B．(1,2)C．(2,-1)D．(1,-2)
3．如图，某研究性学习小组为测量学校A与河对岸工厂B之间的距离，在学校附近选一点C，利用仪器测得∠A=60∘，∠C=90∘，AC=3km.据此，可求得学校与工厂之间的距离AB等于（）.
A．3kmB．5kmC．33kmD．6km
4．已知三角形的两边长分别为5，9，则第三边长可以是（）.
A．15B．14C．4D．5
5．下列运算正确的是（）.
A．2a-a=2B．(x-1)2=x2-1C．a6÷a3=a2D．(2a3)2=4a6
6．小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线。如图：一把直尺压住射线OB，另一把直尺压住射线OA并且与第一把直尺交于点P，小明说：“射线OP就是∠BOA的角平分线.”他这样做的依据是（）.
A．三角形三条角平分线的交点到三条边的距离相等
B．角平分线上的点到这个角两边的距离相等
C．角的内部到角的两边的距离相等的点在角的平分线上
D．以上均不正确
7．下列各式的运算或变形中，用到交换律的是（）.
A．a2⋅a3=a2+3B．(ab)2=a2b2
C．由x+2=5得x=5-2D．3a+2a=5a
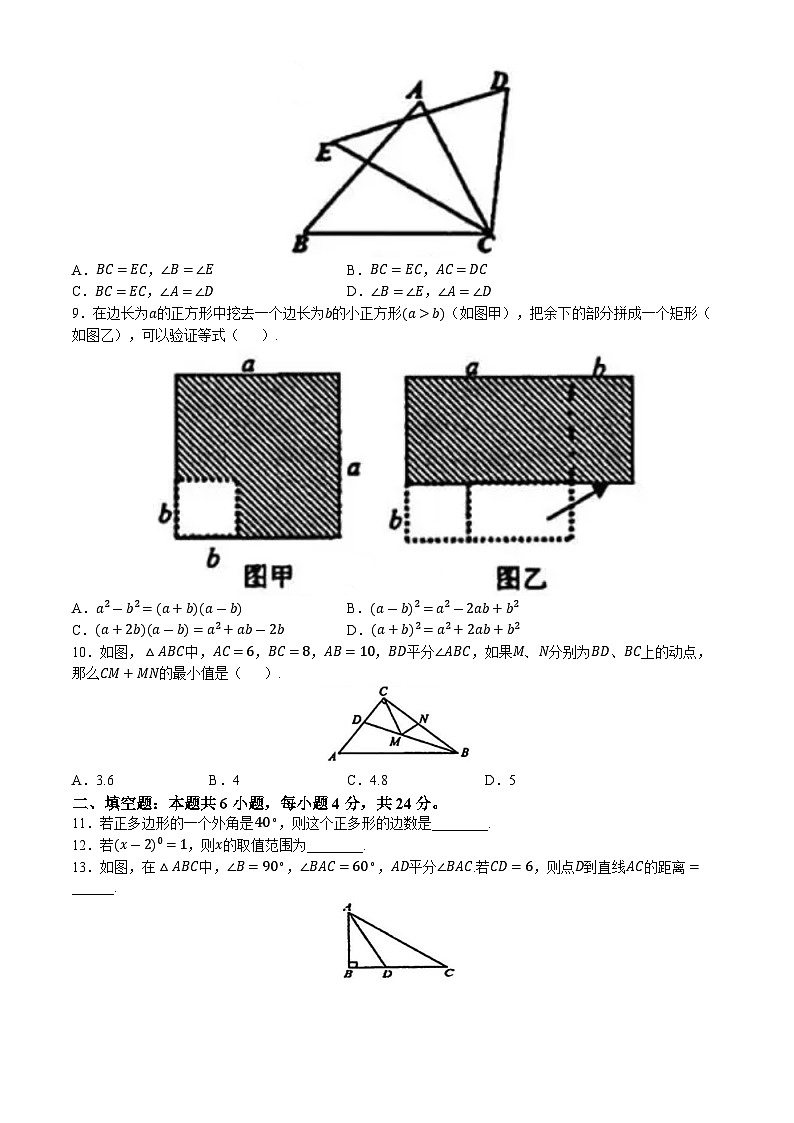
8．如图，在△ABC和△DEC中，已知AB=DE，还需添加两个条件才能使△ABC≅△DEC，不能添加的一组条件是（）.
A．BC=EC，∠B=∠EB．BC=EC，AC=DC
C．BC=EC，∠A=∠DD．∠B=∠E，∠A=∠D
9．在边长为a的正方形中挖去一个边长为b的小正方形(a>b)（如图甲），把余下的部分拼成一个矩形（如图乙），可以验证等式（）.
A．a2-b2=(a+b)(a-b)B．(a-b)2=a2-2ab+b2
C．(a+2b)(a-b)=a2+ab-2bD．(a+b)2=a2+2ab+b2
10．如图，△ABC中，AC=6，BC=8，AB=10，BD平分∠ABC，如果M、N分别为BD、BC上的动点，那么CM+MN的最小值是（）.
A．3.6B．4C．4.8D．5
二、填空题：本题共6小题，每小题4分，共24分。
11．若正多边形的一个外角是40∘，则这个正多形的边数是________.
12．若(x-2)0=1，则x的取值范围为________.
13．如图，在△ABC中，∠B=90∘，∠BAC=60∘，AD平分∠BAC.若CD=6，则点D到直线AC的距离=______.
14．如图，用圆规以直角顶点O为圆心，以适当长度为半径画一条弧交两直角边于A，B两点，若再以A为圆心，以OA为半径画弧，与弧AB交于点C，则∠AOC等于________.
15．若x2-x-1=0，则x3-2x2+2023的值是________.
16．如图在Rt△ABC中，AB=AC，∠BAC=90∘，D、E是BC上两点，且∠DAE=45∘，若BD=2，CE=3，S△ADE=10，则△ABD与△AEC的面积之和为______.
三、解答题：本题共9小题，共86分.解答应写出文字说明、证明过程或演算步.
17．（8分）计算：
（1）3a⋅(-2b)2÷6ab
（2）(x+y)2-(x+y)(x-y)
18．（8分）如图，AD=BC，AC=BD，求证：∠C=∠D.
19．（8分）先化简再求值：(a+b)(a+2b)-(2b3-ab2)÷b，其中a=2，b=-1.
20．（8分）求证：等腰三角形两腰上的高相等.
21．（8分）如图，在△ABC中，AB=AC.
（1）尺规作图：在边BC上找一点D，使得∠BAD=∠B；（不写作法，保留作图痕迹）
（2）在（1）的条件下，若CA=CD，求∠B的度数.
22．（10分）根据完全平方公式(a+b)2=a2+2ab+b2，(a-b)2=a2-2ab+b2
我们可以得出下列结论：ab=12[(a+b)2-(a2+b2)]①，(a-b)2=(a+b)2-4ab②
利用公式①和②解决下列问题：
已知m满足(3m-2025)2+(2024-3m)2=5，
（1）求(3m-2025)(2024-3m)的值；
（2）求(6m-4039)2的值.
23．（10分）如图，在△ABC中，AB=AC，点E在CA延长线上，EP⊥BC于点P，交AB于点F，若AF=2，BF=3，求CE的长度.
24．（12分）如图，在平面直角坐标系中，点A(-8,0)，点B在y轴正半轴上，AB=BC，∠CBA=90∘.
（1）如图1，当B(0,3)时，连接AC交y轴于点D，直接写出点C的坐标；
（2）如图2，DB⊥y轴于B且BD=BO，连接CD交y轴于一点E，在B点运动的过程中，BE的长度是否会发生变化？若不变，求出BE的长度；若变化，请说明理由；
（3）如图3，N在AC延长线上，过N(t,-8)作NQ⊥x轴于Q，探究线段BN、AQ、BO之间的数量关系，并证明你的结论.
25．（14分）如图，在等边△ABC中，D为边AC上一点，延长BD至F使得AF=AC，过A作AH⊥BF于H，AH与FC的延长线交于点G.
（1）若∠CAF为α，直接写出∠AFC的度数；（用含α的代数式表示）
（2）求∠GFH的度数；
（3）已知C为GF的中点，且CD=1.5，求AD的长.