高中数学2.2.3 一元二次不等式的解法导学案及答案

这是一份高中数学2.2.3 一元二次不等式的解法导学案及答案，共9页。

城市人口的急剧增加使车辆日益增多，需要通过修建立交桥和高架道路以提高车速和通过能力．城市环线和高速公路网的连结也必须通过大型互通式立交桥进行分流和引导，保证交通的畅通．城市立交桥已成为现代化城市的重要标志．为了保证安全，交通部门规定，在立交桥的某地段的运行汽车的车距d正比于速度v的平方与车身长(单位：m)的积，且车距不得少于半个车身，假定车身长均为l(单位：m)，当车速为60(单位：km/h)时，车距为1.44个车身长．
[问题] 在交通繁忙时，应规定怎样的车速，才能使此处的车流量最大？



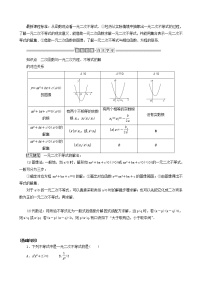
知识点 一元二次不等式的解法
1．一元二次不等式的概念
一般地，形如ax2＋bx＋c>0的不等式称为一元二次不等式，其中a，b，c为常数，而且a≠0.
eq \a\vs4\al()
判断一个不等式是一元二次不等式的关键
(1)只含有一个未知数；
(2)未知数的最高次数为2；
(3)特别要注意二次项的系数不为0.
2．用因式分解法解一元二次不等式
一般地，如果x10(a≠0)通过配方总是可以变为(x－h)2>k或(x－h)2