第02讲 匀变速直线运动的规律（讲义）（解析版）-2025年高考物理一轮复习讲练测（新教材新高考）

这是一份第02讲 匀变速直线运动的规律（讲义）（解析版）-2025年高考物理一轮复习讲练测（新教材新高考），共16页。试卷主要包含了真题练习，命题洞见等内容，欢迎下载使用。
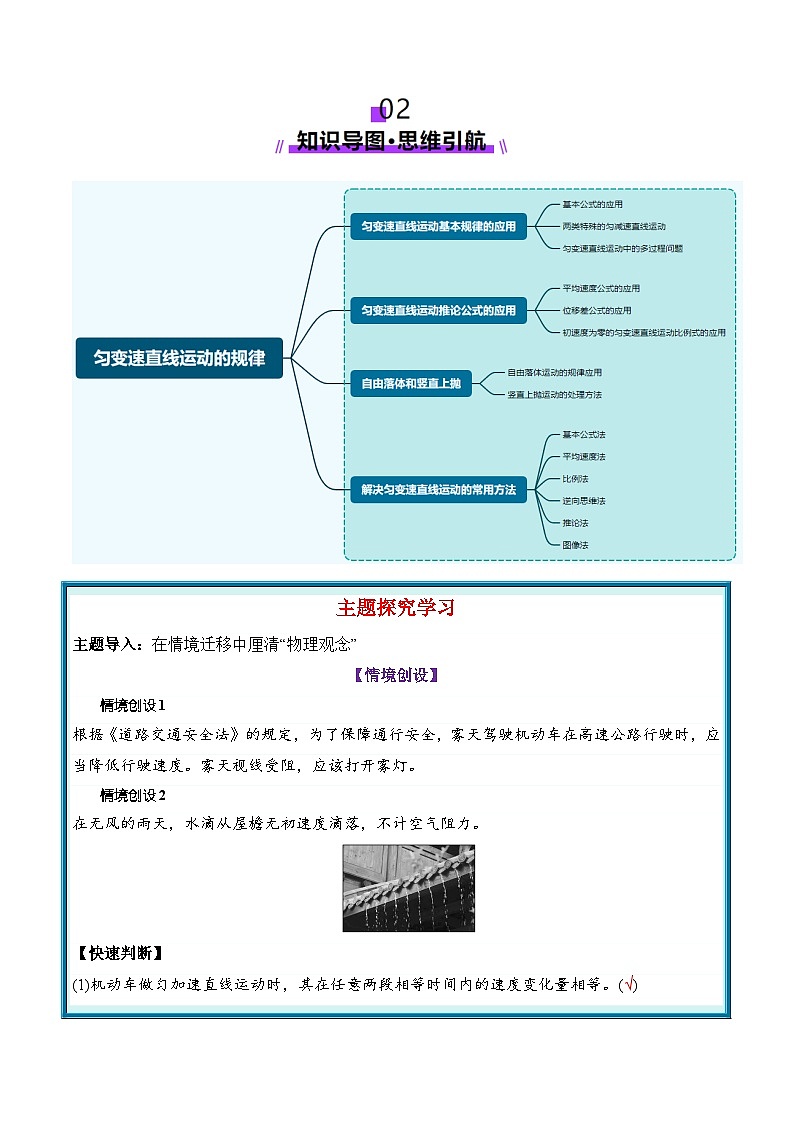
01、考情透视，目标导航TOC \ "1-3" \h \u
02、知识导图，思维引航 \l "_Tc12871" PAGEREF _Tc12871 \h 2
03、考点突破，考法探究 \l "_Tc28128" PAGEREF _Tc28128 \h 3
\l "_Tc24207" 考点一 匀变速直线运动的基本规律及应用 PAGEREF _Tc24207 \h 4
\l "_Tc9640" 考向1 基本公式的应用 PAGEREF _Tc9640 \h 4
\l "_Tc17747" 考向2 两类特殊的匀减速直线运动对比 PAGEREF _Tc17747 \h 7
\l "_Tc26801" 考向3 匀变速直线运动中的多过程问题 PAGEREF _Tc26801 \h 9
\l "_Tc28584" 考点二 匀变速直线运动的推论及应用 PAGEREF _Tc28584 \h 10
\l "_Tc15828" 考向1 平均速度公式的应用 PAGEREF _Tc15828 \h 10
\l "_Tc11680" 考向2 位移差公式的应用 PAGEREF _Tc11680 \h 11
\l "_Tc16580" 考向3初速度为零的匀变速直线运动比例式的应用 PAGEREF _Tc16580 \h 12
\l "_Tc2608" 考点三 自由落体和竖直上抛 PAGEREF _Tc2608 \h 12
\l "_Tc10214" 考向1 自由落体规律的应用 PAGEREF _Tc10214 \h 13
\l "_Tc10280" 考向2 竖直上抛运动的处理方法 PAGEREF _Tc10280 \h 15
\l "_Tc17309" 考点四 解决匀变速直线运动问题的六种方法 PAGEREF _Tc17309 \h 16
\l "_Tc4679" 考向1 基本公式法 PAGEREF _Tc4679 \h 17
\l "_Tc32155" 考向2 平均速度法 PAGEREF _Tc32155 \h 18
\l "_Tc11206" 考向3 比例法 PAGEREF _Tc11206 \h 18
\l "_Tc12157" 考向4 逆向思维法 PAGEREF _Tc12157 \h 19
\l "_Tc7585" 考向5 推论法 PAGEREF _Tc7585 \h 19
\l "_Tc15245" 考向6 图像法 PAGEREF _Tc15245 \h 20
04、真题练习，命题洞见
考点一 匀变速直线运动的基本规律及应用
1.匀变速直线运动
沿着一条直线且加速度不变的运动。如图所示，v－t图线是一条倾斜的直线。
2．匀变速直线运动的两个基本规律
(1)速度与时间的关系式：v＝v0＋at。
(2)位移与时间的关系式：x＝v0t＋eq \f(1,2)at2。
由以上两式联立可得速度与位移的关系式：v2－v02＝2ax。
3．公式选用原则
以上三个公式共涉及五个物理量，每个公式有四个物理量。选用原则如下：
不涉及位移，选用v＝v0＋at
不涉及末速度，选用x＝v0t＋eq \f(1,2)at2
不涉及时间，选用v2－v02＝2ax
4．正方向的选取
以上三式均为矢量式，无论是匀加速直线运动还是匀减速直线运动，通常以初速度v0的方向为正方向；当v0＝0时，一般以加速度a的方向为正方向。速度、加速度、位移的方向与正方向相同时取正，相反时取负。
考向1 基本公式的应用
1.（23-24高三上·湖北·开学考试）一列复兴号动车进站时做匀减速直线运动，车头经过站台上三个立柱A、B、C，对应时刻分别为t1、t2、t3，其x-t图像如图所示。则下列说法正确的是（ ）
A．
B．车头经过立柱A的速度为
C．车头经过立柱B的速度为
D．车头经过立柱A、B过程中的平均速度为
【答案】D
【详解】A．根据初速度为0的匀加速直线运动的推导规律可知，只有初速度为0，连续通过相同位移所需时间的比为，动车做有一定初速度的匀减速运动，故A错误；
B．因为动车做匀减速直线运动，所以车头经过立柱A 的速度为不可能为时间的平均速度，故B错误；
C．时间段的平均速度为，只有匀变速直线运动中间时刻的平均速度等于该段位移内的平均速度，而B点属于该段的位移中点，故C错误；
D．车头经过立柱A、B过程中的平均速度为
故D正确。
故选D。
【题后感悟】
1．公式间的关系
2．公式选取技巧
涉及的物理量
未涉及的物理量
适宜选用公式
v0，v，a，t
x
v＝v0＋at
v0，a，t，x
v
x＝v0t＋eq \f(1,2)at2
v0，v，a，x
t
v2－v02＝2ax
v0，v，t，x
a
x＝eq \f(v＋v0,2)t
【巩固训练】．在女子直线400 m比赛中某段时间内，某同学从静止开始做匀加速直线运动，经t1＝4 s后速度达到v1＝8 m/s，然后匀速运动了t2＝10 s，接着经t3＝5 s匀减速运动到v2＝6 m/s。(该同学可以看作质点)求：
(1)该同学在加速运动阶段的加速度a1；
(2)该同学在第16 s末的速度v3；
(3)该同学这段时间内的位移x。
【答案】 (1)2 m/s2 (2)7.2 m/s (3)131 m
【解析】 (1)设匀加速阶段的加速度为a1，则
v1＝a1t1
解得a1＝2 m/s2。
(2)设减速运动阶段的加速度为a2，因为
v2＝v1＋a2t3
所以a2＝－0.4 m/s2
当t＝16 s时，质点已减速运动了t4＝2 s，此时质点的速度为v3＝v1＋a2t4＝7.2 m/s。
(3)匀加速直线运动的位移x1＝eq \f(1,2)a1teq \\al(2,1)＝16 m
匀速直线运动的位移x2＝v1t2＝80 m
匀减速直线运动的位移x3＝v1t3＋eq \f(1,2)a2teq \\al(2,3)＝35 m
则总位移x＝x1＋x2＋x3＝131 m。
考向2 两类特殊的匀减速直线运动对比
2.汽车在水平面上刹车,其位移与时间的关系是x=24t-6t2,则它在前3s内的平均速度为( ）
A．6 m/sB．8 m/sC．10 m/sD．12 m/s
【答案】B
【详解】由位移与时间的关系可知，
v0=24m/s；a=-12m/s2
则由v=v0+at可知，汽车在2s末即静止，故3s内的位移等于2s内的位移，故3s内汽车的位移
则汽车的平均速度
A．6m/s与分析不符，故A错误；
B．8m/s与分析相符，故B正确；
C．10m/s与分析不符，故C错误；
D．12m/s与分析不符，故D错误．
3．如图所示，一物块（可视为质点）以一定的初速度从一足够长的光滑固定斜面的底端开始上滑，在上滑过程中的最初5s内和最后5s内经过的位移之比为11：5．忽略空气阻力，则此物块从底端开始上滑到返回斜面底端一共经历的时间是（ ）
A．8sB．10sC．16sD．20s
【答案】C
【详解】设物体运动的加速度为a，上滑运动总时间为t，把物体上滑的运动看成反向的初速度为0的匀加速直线运动，则有：最后5s内位移为
s1＝a×52＝a
最初5s内位移为
又因为
s2：s1=11：5
解得
t=8s
由于斜面光滑，上滑和下滑的时间相同，则物块从底端开始上滑到返回斜面底端一共经历的时间是16s。
故选C。
【题后感悟】
两类特殊的匀减速直线运动分析
刹车类
(1)其特点为匀减速到速度为零后即停止运动，加速度a突然消失。
(2)求解时要注意确定其实际运动时间。
(3)如果问题涉及最后阶段(到停止运动)的运动，可把该阶段看成反向的初速度为零的匀加速直线运动。
双向可逆类
(1)示例：如沿光滑斜面上滑的小球，到最高点后仍能以原加速度匀加速下滑，全过程加速度大小、方向均不变。
(2)注意：求解时可分过程列式也可对全过程列式，但必须注意x、v、a等矢量的正负号及物理意义。
【巩固训练】．具有“主动刹车系统”的汽车遇到紧急情况时，会立即启动主动刹车。某汽车以28 m/s的速度匀速行驶时，前方50 m处突然出现一群羚羊横穿公路，“主动刹车系统”立即启动，汽车开始做匀减速直线运动，恰好在羚羊通过道路前1 m处停车。汽车开始“主动刹车”后第4 s内通过的位移大小为( )
A.0 B.1 m
C.2 m D.3 m
【答案】 B
【解析】 令x1＝50 m，x2＝1 m，汽车的刹车时间为t，刹车时的加速度大小为a，把刹车过程逆向处理，则有veq \\al(2,0)＝2a(x1－x2)，t＝eq \f(v0,a)，联立解得a＝8 m/s2，t＝3.5 s，所以汽车开始“主动刹车”后第4 s内通过的位移大小为3～3.5 s内通过的位移大小，有x4＝eq \f(1,2)aΔt2，解得x4＝1 m，故B正确。
考向3 匀变速直线运动中的多过程问题
4.因高铁的运行速度快，对制动系统的性能要求较高，高铁列车上安装有多套制动装置——制动风翼、电磁制动系统、空气制动系统、摩擦制动系统等。在一段直线轨道上，某高铁列车正以v0=288km/h的速度匀速行驶，列车长突然接到通知，前方x0=5km处道路出现异常，需要减速停车。列车长接到通知后，经过t1=2.5s将制动风翼打开，高铁列车获得a1=0.5m/s2的平均制动加速度减速，减速t2=40s后，列车长再将电磁制动系统打开，结果列车在距离异常处500m的地方停下来。
（1）求列车长打开电磁制动系统时，列车的速度的大小。
（2）求制动风翼和电磁制动系统都打开时，列车的平均制动加速度a2的大小。
【答案】（1）60m/s；（2）1.2m/s2
【详解】（1）打开制动风翼时，列车的加速度大小为a1=0.5m/s2，设经过t2=40s时，列车的速度为v1，根据速度-时间公式，有
代入数据解得
（2）列车长接到通知后，经过，列车行驶的距离
打开制动风翼到打开电磁制动系统的过程中，根据速度-位移公式
解得列车行驶的距离
打开电磁制动后，列车行驶的距离
根据速度-位移公式
可得
【题后感悟】
求解多过程运动问题的方法
(1)根据题意画出物体在各阶段的运动示意图，直观呈现物体的运动过程。
(2)明确物体在各阶段的运动性质，找出题目给定的已知量、待求量以及中间量。
(3)合理选择运动学公式，列出物体在各阶段的运动方程，同时列出物体各阶段间的关联方程，联立求解。
【注意】物体前一阶段的末速度是后一阶段的初速度，即速度是联系各阶段运动的桥梁。
考点二 匀变速直线运动的推论及应用
1．匀变速直线运动的常用推论
(1)平均速度公式：做匀变速直线运动的物体在一段时间内的平均速度等于这段时间内初、末时刻速度矢量和的一半，还等于中间时刻的瞬时速度。即：eq \x\t(v)＝eq \f(v0＋v,2)＝。此公式可以求某时刻的瞬时速度。
(2)位移差公式：连续相等的相邻时间间隔T内的位移差相等。
即：Δx＝x2－x1＝x3－x2＝…＝xn－xn－1＝aT2。
不相邻相等的时间间隔T内的位移差xm－xn＝(m－n)aT2，此公式可以求加速度。
2．初速度为零的匀加速直线运动的四个重要比例式
(1)T末、2T末、3T末、…、nT末的瞬时速度之比为v1∶v2∶v3∶…∶vn＝1∶2∶3∶…∶n。
(2)前T内、前2T内、前3T内、…、前nT内的位移之比为x1∶x2∶x3∶…∶xn＝1∶4∶9∶…∶n2。
(3)第1个T内、第2个T内、第3个T内、…、第n个T内的位移之比为xⅠ∶xⅡ∶xⅢ∶…∶xN＝1∶3∶5∶…∶(2n－1)。
(4)从静止开始通过连续相等的位移所用时间之比为t1∶t2∶t3∶…∶tn＝1∶(eq \r(2)－1)∶(eq \r(3)－eq \r(2))∶…∶(eq \r(n)－eq \r(n－1))。
考向1 平均速度公式的应用
1.(2023·山东卷，6)如图所示，电动公交车做匀减速直线运动进站，连续经过R、S、T三点，已知ST间的距离是RS的两倍，RS段的平均速度是10 m/s，ST段的平均速度是5 m/s，则公交车经过T点时的瞬时速度为( )
A.3 m/s B.2 m/s
C.1 m/s D.0.5 m/s
【答案】 C
【解析】 由题知，电动公交车做匀减速直线运动，设RS间的距离为x，公交车经过R、S、T点时瞬时速度为v1、v2、v3，经过RS间的时间为t1，经过ST间的时间为t2，有eq \f(v1＋v2,2)＝10 m/s，eq \f(v2＋v3,2)＝5 m/s，则v1－v3＝10 m/s，又eq \f(x,t1)＝10 m/s，eq \f(2x,t2)＝5 m/s，则t1＋t2＝eq \f(x,2)，全程的平均速度eq \(v,\s\up6(－))＝eq \f(3x,t1＋t2)＝6 m/s，即eq \f(v1＋v3,2)＝6 m/s，联立解得v3＝1 m/s，故C正确。
考向2 位移差公式的应用
2. (2024·辽宁鞍山市模拟)如图所示为一辆无人送货车正在做匀加速直线运动。某时刻起开始计时，在第一个4 s内位移为9.6 m，第二个4 s内位移为16 m，下列说法正确的是( )
A.计时时刻送货车的速度为0
B.送货车的加速度大小为1.6 m/s2
C.送货车在第1个4 s末的速度大小为3.2 m/s
D.送货车在第2个4 s内的平均速度大小为3.6 m/s
【答案】 C
【解析】 根据匀变速直线运动推论可得加速度大小为a＝eq \f(Δx,T2)＝eq \f(16－9.6,42) m/s2＝0.4 m/s2，B错误；根据匀变速直线运动中间时刻的瞬时速度等于该段内的平均速度可知送货车在第1个4 s末的速度大小为v1＝eq \f(x1＋x2,2T)＝eq \f(9.6＋16,8) m/s＝3.2 m/s，C正确；根据v＝v0＋at可得，计时时刻送货车的速度为v0＝v1－aT＝3.2 m/s－0.4×4 m/s＝1.6 m/s，A错误；送货车在第2个4 s内的平均速度大小为eq \(v,\s\up6(－))＝eq \f(x2,T)＝eq \f(16,4) m/s＝4 m/s, D错误。
考向3初速度为零的匀变速直线运动比例式的应用
3 (多选)如图所示，将完全相同的水球紧挨在一起水平排列，子弹在水球中沿水平方向视为做匀变速直线运动，某次实验中，子弹恰好能穿出第四个水球，则( )
A.由题目信息可以求得子弹穿过每个水球的时间之比(eq \r(4)－eq \r(3))∶(eq \r(3)－eq \r(2))∶(eq \r(2)－eq \r(1))∶1
B.子弹在每个水球中运动的平均速度相同
C.子弹在每个水球中速度变化量相同
D.子弹依次进入四个水球的初速度之比为eq \r(4)∶eq \r(3)∶eq \r(2)∶eq \r(1)
【答案】 AD
【解析】 将子弹的运动过程逆向来看，即看成从左到右做初速度为零的匀加速直线运动，根据初速度为零的匀加速运动在连续相等的位移所用时间之比为1∶(eq \r(2)－1)∶(eq \r(3)－eq \r(2))∶(2－eq \r(3))∶…可知，子弹从右到左穿过每个水球的时间之比为(eq \r(4)－eq \r(3))∶(eq \r(3)－eq \r(2))∶(eq \r(2)－eq \r(1))∶1，A正确；根据A项分析子弹在每个水球中运动的时间不同，位移大小相同，所以平均速度不同，B错误；根据公式Δv＝aΔt知，子弹在每个水球中运动的速度变化量不同，C错误；根据速度与位移的关系式有v2＝2ax，则v＝eq \r(2ax)，设在每个水球中的位移大小为x0，可得子弹从左到右每次射出水球的速度之比为eq \r(2ax0)∶eq \r(2a·2x0)∶eq \r(2a·3x0)∶eq \r(2a·4x0)＝1∶eq \r(2)∶eq \r(3)∶2，即子弹从右到左减速过程依次进入四个水球的初速度之比为eq \r(4)∶eq \r(3)∶eq \r(2)∶1，D正确。
考点三 自由落体和竖直上抛
一．自由落体运动
1．条件：物体只受重力，从静止开始下落。
2．运动性质：初速度为零、加速度为g 的匀加速直线运动。
3．基本规律：
(1)速度与时间的关系式：v＝gt。
(2)位移与时间的关系式：h＝eq \f(1,2)gt2。
(3)速度位移关系式：v2＝2gh。
二．竖直上抛运动
1．运动特点：初速度方向竖直向上，加速度为g，上升阶段做匀减速直线运动，下降阶段做自由落体运动。
2．运动性质：匀变速直线运动。
3．基本规律
(1)速度与时间的关系式：v＝v0－gt。
(2)位移与时间的关系式：x＝v0t－eq \f(1,2)gt2。
4．竖直上抛运动的对称性(如图所示)
(1)时间对称：物体上升过程中从A→C所用时间tAC和下降过程中从C→A所用时间tCA相等，同理tAB＝tBA。
(2)速度对称：物体上升过程经过A点的速度与下降过程经过A点的速度大小相等。
考向1 自由落体规律的应用
1.如图所示，一个小孩在公园里玩“眼疾手快”游戏。游戏者需接住从支架顶部随机落下的圆棒。已知支架顶部距离地面2.3 m，圆棒长0.4 m，小孩站在支架旁边，手能触及所有圆棒的下落轨迹的某一段范围AB，上边界A距离地面1.1 m，下边界B距离地面0.5 m。不计空气阻力，重力加速度。求：
（1）圆棒下落到A点所用的时间；
（2）圆棒通过AB所用的时间；
（3）结合轨迹反应时间（判断棒下落轨迹的时间）和握棒反应时间（棒经过某点的时间）应用自由落体运动知识简要分析在A点和B点接棒各自的优缺点。
【答案】（1）；（2）；（3）见解析
【详解】（1）圆棒底部距离A点高度
圆棒做自由落体运动下落到A点有
代入数据解得
（2）圆棒通过AB的过程即圆棒底部到达A点和圆棒顶端离开B点这一过程，可知圆棒底部到达A点的速度为
圆棒通过AB下落的高度为
圆棒通过AB过程由
代入数据解得
（3）A点握棒的优点：圆棒下落到A点时速度较小，通过A点所有的时间稍长，如果握棒反应时间较长，也利于抓住圆棒；
A点握棒的缺点：圆棒下落到A点所用时间较短，若反应速度较慢，很容易错过抓棒机会；
B点握棒的优点：圆棒下落到B点所用时间较长，即使反应速度较慢，也有足够的反应时间做好抓棒准备，可以提高抓棒的成功率；
B点握棒的缺点：圆棒下落到B点时速度较大，通过B点所有的时间较短，如果握棒反应时间较长，很难抓住圆棒。
【题后感悟】
1.运动特点
初速度为0，加速度为g的匀加速直线运动。
2.解题方法
(1)初速度为0的匀变速直线运动规律都适用。
①从开始下落，连续相等时间内下落的高度之比为1∶3∶5∶7∶…。
②由Δv＝gΔt知，相等时间内，速度变化量相同。
③连续相等时间T内下落的高度之差Δh＝gT2。
(2)物体由静止开始的自由下落过程才是自由落体运动，从中间截取的一段运动过程不是自由落体运动，等效于竖直下抛运动，应该用初速度不为零的匀变速直线运动规律去解决此类问题。
考向2 竖直上抛运动的处理方法
2．为测试一物体的耐摔性，在离地25 m高处，将其以20 m/s的速度竖直向上抛出，重力加速度g＝10 m/s2，不计空气阻力，求：
(1)经过多长时间到达最高点；
(2)抛出后离地的最大高度是多少；
(3)经过多长时间回到抛出点；
(4)经过多长时间落到地面；
(5)经过多长时间离抛出点15 m。
【答案 (1)2 s (2)45 m (3)4 s (4)5 s(5)1 s 3 s (2＋eq \r(7))s
【解析 (1)运动到最高点时速度为0，
由v＝v0－gt1得t1＝－eq \f(v－v0,g)＝eq \f(v0,g)＝2 s
(2)由v02＝2ghmax得hmax＝eq \f(v02,2g)＝20 m，
所以Hmax＝hmax＋h0＝45 m
(3)法一：分段，由(1)(2)知上升时间t1＝2 s，
hmax＝20 m，下落时，hmax＝eq \f(1,2)gt22，
解得t2＝2 s，故t＝t1＋t2＝4 s
法二：由对称性知返回抛出点时速度为20 m/s，方向向下，则由v1＝v0－gt，得t＝－eq \f(v1－v0,g)＝4 s
法三：由h＝v0t－eq \f(1,2)gt2，令h＝0，
解得t3＝0(舍去)，t4＝4 s
(4)法一：分段法
由Hmax＝eq \f(1,2)gt52，解得t5＝3 s，故t总＝t1＋t5＝5 s
法二：全程法
由－h0＝v0t′－eq \f(1,2)gt′2
解得t6＝－1 s(舍去)，t7＝5 s
(5)当物体在抛出点上方时，h＝15 m，
由h＝v0t－eq \f(1,2)gt2，解得t8＝1 s，t9＝3 s，
当物体在抛出点下方时，h＝－15 m，由h＝v0t－eq \f(1,2)gt2，得t10＝(2＋eq \r(7)) s，t11＝(2－eq \r(7)) s(舍去)。
【题后感悟】
1．竖直上抛运动的研究方法：
分段法
上升阶段：a＝g的匀减速直线运动
下降阶段：自由落体运动
全程法
初速度v0向上，加速度g向下的匀变速直线运动，v＝v0－gt，h＝v0t－eq \f(1,2)gt2(以竖直向上为正方向)
若v>0，物体上升，若v0，物体在抛出点上方，若h