

第14讲 抛体运动(讲义)(解析版)-2025年高考物理一轮复习讲练测(新教材新高考)
展开
这是一份第14讲 抛体运动(讲义)(解析版)-2025年高考物理一轮复习讲练测(新教材新高考),共29页。
\l "_Tc8419" 02、知识导图,思维引航 PAGEREF _Tc8419 \h 3
\l "_Tc916" 03、考点突破,考法探究 PAGEREF _Tc916 \h 3
\l "_Tc31522" 考点一 平抛运动规律及应用 PAGEREF _Tc31522 \h 3
\l "_Tc31110" 知识点1、平抛运动 PAGEREF _Tc31110 \h 3
\l "_Tc17245" 知识点2、平抛运动的规律 PAGEREF _Tc17245 \h 4
\l "_Tc31298" 知识点3、平抛运动时间和水平射程 PAGEREF _Tc31298 \h 4
\l "_Tc11782" 知识点4.速度和位移的变化规律 PAGEREF _Tc11782 \h 5
\l "_Tc2130" 考向1 单物体的平抛运动 PAGEREF _Tc2130 \h 5
\l "_Tc23511" 考点2 多物体的平抛运动 PAGEREF _Tc23511 \h 6
\l "_Tc12407" 考点二 与斜面或圆弧面有关的平抛运动 PAGEREF _Tc12407 \h 6
\l "_Tc10875" 考向1 与斜面有关的平抛运动 PAGEREF _Tc10875 \h 8
\l "_Tc15559" 考向2.与圆弧面有关的平抛运动 PAGEREF _Tc15559 \h 10
\l "_Tc31141" 考点三 平抛运动的临界、极值问题 PAGEREF _Tc31141 \h 11
\l "_Tc15224" 知识点1、常见的“临界术语” PAGEREF _Tc15224 \h 11
\l "_Tc20906" 知识点2、平抛运动临界、极值问题的分析方法 PAGEREF _Tc20906 \h 12
\l "_Tc27730" 考向1 物体达到最大位移、最小位移、最大初速度、最小初速度 PAGEREF _Tc27730 \h 12
\l "_Tc29758" 考向2 物体的速度方向恰好沿某一方向时 PAGEREF _Tc29758 \h 13
\l "_Tc7474" 考点四 斜抛运动 PAGEREF _Tc7474 \h 13
\l "_Tc12386" 知识点1、斜抛运动的基本概念 PAGEREF _Tc12386 \h 13
\l "_Tc7196" 知识点2、斜抛运动的基本规律 PAGEREF _Tc7196 \h 14
\l "_Tc1083" 考向1 斜抛运动规律的理解和应用 PAGEREF _Tc1083 \h 14
\l "_Tc5818" 考向2 三维空间内的斜抛运动 PAGEREF _Tc5818 \h 16
\l "_Tc13562" 考向3 斜抛运动与斜面结合问题 PAGEREF _Tc13562 \h 16
\l "_Tc12720" 04、真题练习,命题洞见 PAGEREF _Tc12720 \h 18
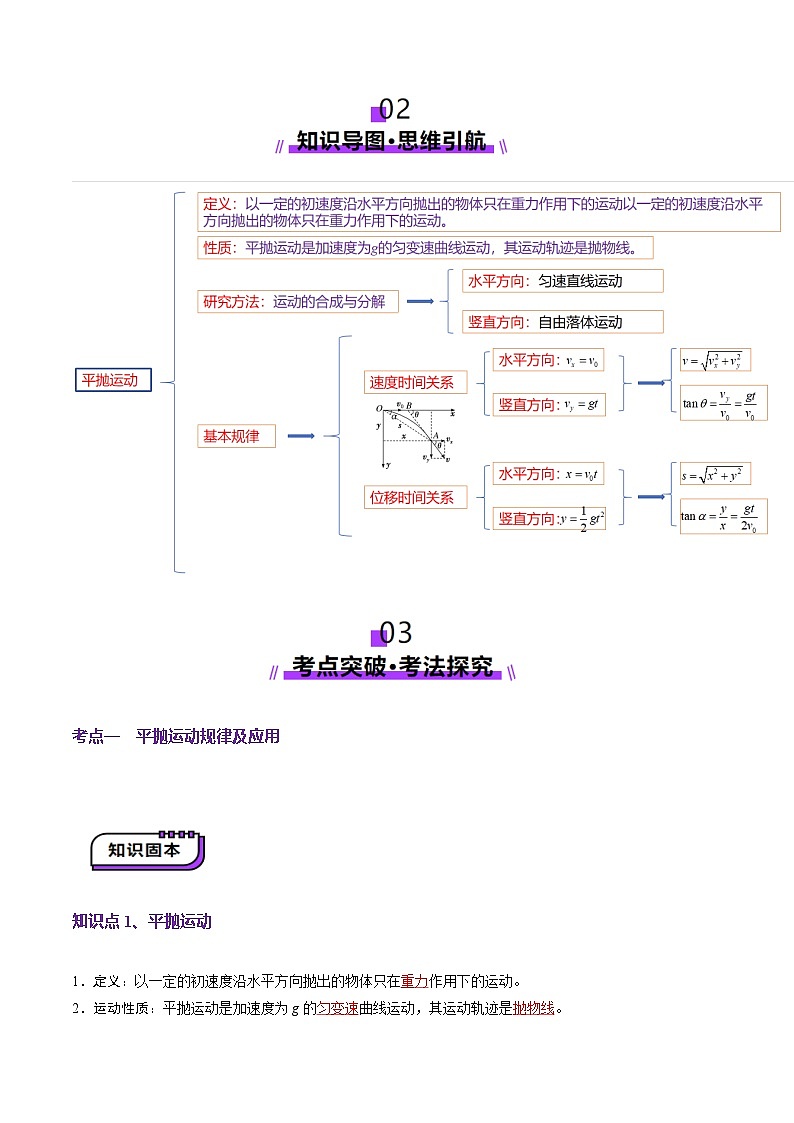
考点一 平抛运动规律及应用
知识点1、平抛运动
1.定义:以一定的初速度沿水平方向抛出的物体只在重力作用下的运动。
2.运动性质:平抛运动是加速度为g的匀变速曲线运动,其运动轨迹是抛物线。
3.研究方法——运动的合成与分解。
(1)水平方向:匀速直线运动;
(2)竖直方向:自由落体运动。
知识点2、平抛运动的规律
知识点3、平抛运动时间和水平射程
知识点4.速度和位移的变化规律
考向1 单物体的平抛运动
1 (多选)摩托车跨越表演是一项惊险刺激的运动,受到许多极限爱好者的喜爱。假设在一次跨越河流的表演中,摩托车离开平台时的速度为24 m/s,刚好成功落到对面的平台上,测得两岸平台高度差为5 m,如图3所示。若飞越中不计空气阻力,摩托车可以近似看成质点,g取10 m/s2,则下列说法正确的是( )
A.摩托车在空中的飞行时间为1 s
B.河宽为24 m
C.摩托车落地前瞬间的速度大小为10 m/s
D.若仅增加平台的高度(其他条件均不变),摩托车依然能成功跨越此河流
【答案】 ABD
【解析】 摩托车在竖直方向做自由落体运动,则有h=eq \f(1,2)gt2,解得摩托车在空中的飞行时间为t=1 s,故A正确;河流的宽度即摩托车水平方向位移为d=x=v0t=24×1 m=24 m,故B正确;竖直方向速度为vy=gt=10 m/s,则摩托车落地前瞬间的速度为v=eq \r(veq \\al(2,0)+veq \\al(2,y))=eq \r(242+102) m/s=26 m/s,故C错误;摩托车离开平台做平抛运动,仅增加平台的高度(其他条件均不变),则在空中的飞行时间增大,摩托车水平方向位移增大,所以摩托车依然能成功跨越此河流,故D正确。
考点2 多物体的平抛运动
2. 如图所示,A、B两个小球在同一竖直线上,离地高度分别为2h和h,将两球水平抛出后,不计空气阻力,两球落地时的水平位移分别为s和2s。重力加速度为g,则下列说法正确的是( )
A.A、B两球的初速度大小之比为1∶4
B.A、B两球的运动时间之比为1∶eq \r(2)
C.两小球运动轨迹交点的水平位移为eq \f(5,7)s
D.两小球运动轨迹交点的离地高度为eq \f(6,7)h
【答案】 D
【解析】 小球做平抛运动,竖直方向有H=eq \f(1,2)gt2,解得t=eq \r(\f(2H,g)),则A球运动时间tA=eq \r(\f(2×2h,g))=eq \r(\f(4h,g)),B球运动时间tB=eq \r(\f(2h,g)),所以tA∶tB=eq \r(2)∶1;由x=v0t得v0=eq \f(x,t),结合两球落地时位移之比xA∶xB=1∶2,可知A、B两球的初速度之比为1∶2eq \r(2),故A、B错误;两球相交时,水平方向位移相同,因此有vAtA′=vBtB′,B球下落高度hB=eq \f(1,2)gtB′2,A球下落的高度hA=eq \f(1,2)gtA′2,hA=h+hB,联立各式得hB=eq \f(1,7)h,tB′=eq \r(\f(2h,7g)),则两小球运动轨迹交点的高度为h-eq \f(1,7)h=eq \f(6,7)h,两小球运动轨
迹交点的水平位移xB′=vBtB′,2s=vBeq \r(\f(2h,g)),联立解得xB′=eq \f(2s,\r(7)),C错误,D正确。
考点二 与斜面或圆弧面有关的平抛运动
考向1 与斜面有关的平抛运动
1.近年来,国家大力开展冰雪运动进校园活动,蹬冰踏雪深受学生喜爱。如图所示,两名滑雪运动员(均视为质点)从跳台a处先后沿水平方向向左飞出,其速度大小之比为v1∶v2=2∶1,不计空气阻力,重力加速度为g,则两名运动员从飞出至落到斜坡(可视为斜面)上的过程中,下列说法正确的是( )
A.他们飞行时间之比为t1∶t1=1∶2
B.他们飞行的水平位移之比为x1∶x2=2∶1
C.他们速度变化之比为Δv1∶Δv2=2∶1
D.他们在空中离坡面的最大距离之比为s1∶s2=2∶1
【答案】 C
【解析】 运动员从跳台a处水平飞出,设初速度为v0,飞行时间为t,斜坡的倾角为θ,运动员在空中做平抛运动,落到斜坡上时有tan θ=eq \f(y,x)=eq \f(\f(1,2)gt2,v0t),解得t=eq \f(2v0tan θ,g),可得他们飞行时间之比为t1∶t2=v1∶v2=2∶1,A错误;运动员飞行的水平位移为x=v0t=eq \f(2veq \\al(2,0)tan θ,g),所以他们飞行的水平位移之比为x1∶x2=veq \\al(2,1)∶veq \\al(2,2)=4∶1,B错误;两运动员在水平方向的速度不变,在竖直方向的速度变化为Δvy=gt,因为他们飞行时间之比为t1∶t2=2∶1,则他们速度变化之比为Δv1∶Δv2=t1∶t2=2∶1,C正确;运动员在空中离坡面的最大距离为s=eq \f((v0sin θ)2,2gcs θ),他们在空中离坡面的最大距离之比为s1∶s2=veq \\al(2,1)∶veq \\al(2,2)=4∶1,D错误。
【题后反思】从斜面上某点水平抛出,又落到斜面上的平抛运动
两种
特殊
状态
落回斜面的时刻
速度与斜面平行的时刻
处理
方法
分解位移
分解速度
运动
特征
①位移偏转角度等于斜面倾角θ;
②落回斜面上时速度方向与斜面的夹角与初速度大小无关,只与斜面的倾角有关;
③落回斜面上时的水平位移与初速度的平方成正比,即x∝veq \\al(2,0)
①竖直分速度与水平分速度的比值等于斜面倾角的正切值;
②该时刻是运动全过程的中间时刻;
③该时刻物体距斜面最远
运动
时间
由tan θ=eq \f(y,x)=eq \f(gt,2v0)得t=eq \f(2v0tan θ,g)
由tan θ=eq \f(vy,vx)=eq \f(gt,v0)得t=eq \f(v0tan θ,g)
2. A、D分别是斜面的顶端、底端,B、C是斜面上的两个点,AB=BC=CD,E点在D点的正上方,与A等高,从E点水平抛出质量相等的两个小球,球1落在B点,球2落在C点,忽略空气阻力。关于球1和球2从抛出到落在斜面上的运动过程( )
A.球1和球2运动的时间之比为2∶1
B.球1和球2运动的时间之比为1∶2
C.球1和球2抛出时初速度之比为2∶1
D.球1和球2运动时单位时间内速度变化量之比为1∶1
【答案】 D
【解析】 因为AC=2AB,所以球2的竖直位移是球1竖直位移的2倍,根据h=eq \f(1,2)gt2得t=eq \r(\f(2h,g)),解得运动的时间之比为t1∶t2=1∶eq \r(2),故A、B错误;因为BD=2CD,所以球1的水平位移是球2水平位移的2倍,根据x=v0t得v0=xeq \r(\f(g,2h)),解得初速度之比为v01:v02=2eq \r(2)∶1,故C错误;单位时间内速度变化量即为加速度,而平抛运动的加速度都为g,相同,故D正确。
【题后反思】
方法总结 平抛运动与斜面结合的三种模型
模型
处理
方法
分解速度
分解速度
分解位移
运动
时间
由tan θ=eq \f(vx,vy)=eq \f(v0,gt)得t=eq \f(v0,gtan θ)
由tan θ=eq \f(vy,vx)=eq \f(gt,v0)得t=eq \f(v0tan θ,g)
由tan θ=eq \f(x,y)=eq \f(v0t,\f(1,2)gt2)=eq \f(2v0,gt)得t=eq \f(2v0,gtan θ)
考向2.与圆弧面有关的平抛运动
3.如图所示,半径为R的半球形碗固定于水平面上,碗口水平,O点为碗的圆心,A、B为水平直径的两个端点。将一弹性小球(可视为质点)从A点沿AB方向以初速度v1水平抛出,小球与碗内壁碰撞一次后恰好经过B点;若将该小球从离O点eq \f(\r(3),2)R处的C点以初速度v2水平抛出,小球与碗内壁碰撞一次后恰好返回C点。假设小球与碗内壁碰撞前后瞬间小球的切向速度不变,沿半径方向的速度等大反向,则v2与v1的比值为( )
A.2eq \r(3) B.eq \r(6)
C.eq \r(5) D.eq \r(3)
【答案】B
【解析】小球从A点以初速度v1向右平抛,反弹后经过B点,由对称性知小球与碗内壁的碰撞点应在碗的最低点,由平抛运动的规律有R=v1t1,R=eq \f(1,2)gt12,解得v1=eq \r(\f(1,2)gR);小球从C点以初速度v2向右平抛,要使小球能反弹回C点,小球必须垂直打在圆弧上,
如图所示
设碰撞点为D,连接OD,即为平抛轨迹过D点的切线,过D点作DE⊥AB于E,则O为小球平抛水平位移的中点,有ED=eq \f(1,2)gt22,CO=OE=eq \f(1,2)v2t2,在Rt△ODE中,有(ED)2+(OE)2=R2,解得v2=eq \r(3gR),可得eq \f(v2,v1)=eq \r(6),故选B。
4.如图所示,在竖直平面内有一曲面,曲面满足的数学关系式为y=x2(x>0),在y轴上有一点P,坐标为(0,6 m)。从P点将一可看成质点的小球水平抛出,初速度为1 m/s。则小球第一次打在曲面上的时间为(不计空气阻力,g取10 m/s2)( )
A.1 s B.eq \f(\r(5),5) s C.eq \f(\r(10),2) s D.eq \f(\r(2),2) s
【答案】 A
【解析】 设小球经过时间t打在曲面上M点,M点坐标为(x1,y1),小球水平抛出后做平抛运动,在水平方向上,有x1=v0t,在竖直方向上,有6 m-y1=eq \f(1,2)gt2,又小球打在曲面上,则满足数学关系式y1=x12,代入数据联立解得t=1 s,故A正确,B、C、D错误。
【题后反思】平抛运动与两类曲面结合问题
(1)物体平抛后落入圆弧内时,物体平抛运动的水平位移、竖直位移与圆弧半径存在一定的数量关系。
(2)物体平抛后落入抛物面内时,物体平抛运动的水平位移、竖直位移与抛物线方程结合可以建立水平方向和竖直方向的关系方程。
考点三 平抛运动的临界、极值问题
知识点1、常见的“临界术语”
(1)题目中有“刚好”“恰好”“正好”“取值范围”“多长时间”“多大距离”等词语,表明题述的过程中存在临界点。
(2)题目中有“最大”“最小”“至多”“至少”等字眼,表明题述的过程中存在着极值。
知识点2、平抛运动临界、极值问题的分析方法
(1)确定研究对象的运动性质;
(2)根据题意确定临界状态;
(3)确定临界轨迹,画出轨迹示意图;
(4)应用平抛运动的规律结合临界条件列方程求解。
考向1 物体达到最大位移、最小位移、最大初速度、最小初速度
1.(多选)“山西刀削面”堪称天下一绝,如图所示,小面圈(可视为质点)从距离开水锅高为h处被水平削离,与锅沿的水平距离为L,锅的半径也为L。忽略空气阻力,且小面圈都落入锅中,重力加速度为g,则下列关于所有小面圈在空中运动的描述正确的是( )
A.运动的时间都相同
B.速度的变化量不相同
C.落入锅中时,最大速度是最小速度的3倍
D.若小面圈刚被抛出时初速度为v0,则Leq \r(\f(g,2h))
相关试卷
这是一份第31讲 机械波(讲义)(解析版)-2025年高考物理一轮复习讲练测(新教材新高考),共32页。
这是一份第19讲 功与功率(讲义)(解析版)-2025年高考物理一轮复习讲练测(新教材新高考),共25页。
这是一份第14讲 抛体运动(练习)(原卷版)-2025年高考物理一轮复习讲练测(新教材新高考),共13页。










