人教版第二册下B空间向量复习ppt课件

这是一份人教版第二册下B空间向量复习ppt课件，共42页。PPT课件主要包含了简单几何体1，简单几何体2，简单几何体3，πrl，πr1＋r2l，πR2，切问题1，长方体与球，切问题2，棱锥与球等内容，欢迎下载使用。
第七章立体几何与空间向量
2.圆柱、圆锥、圆台的侧面展开图及侧面积公式
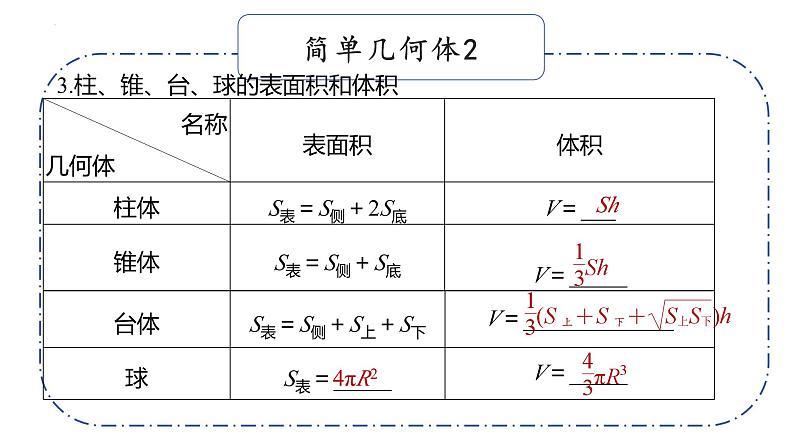
3.柱、锥、台、球的表面积和体积
4.求空间几何体的体积的常用方法
1.正方体与球①内切球：内切球直径2R＝正方体的 .②棱切球：棱切球直径2R＝正方体的 .③外接球：外接球直径2R＝正方体体的 .
②外接球:外接球球心在其高上，底面正多边形的外接圆圆心为E，半径为r，R2＝ (正棱锥外接球半径为R，高为h).
6.R2＝ (R是圆锥外接球的半径，h是圆锥的高，r是圆锥底面圆的半径).
1.正方体与球①内切球：内切球直径2R＝正方体棱长a.②棱切球：棱切球直径2R＝正方体的面对角线长③外接球：外接球直径2R＝正方体体对角线长
②外接球:外接球球心在其高上，底面正多边形的外接圆圆心为E，半径为r，R2＝(h－R)2＋r2(正棱锥外接球半径为R，高为h).
6.R2＝(h－R)2＋r2(R是圆锥外接球的半径，h是圆锥的高，r是圆锥底面圆的半径).
1.基本事实①过 的三个点，有且只有一个平面.②如果一条直线上的 在一个平面内，那么这条直线在这个平面内.③如果两个不重合的平面有一个公共点，那么它们有且只有 过该点的公共直线. ④平行于同一条直线的两条直线 .
2.“三个”推论推论1：经过一条直线和这条直线外一点， 个平面.推论2：经过两条 直线，有且只有一个平面.推论3：经过两条 直线，有且只有一个平面.
3.空间中直线与直线的位置关系
直线：在同一平面内，有且只有一个公共点； 直线：在同一平面内，没有公共点；
异面直线：不同在 一个平面内，没有公共点.
4.等角定理:若空间中两个角的两条边分别对应平行,那么这两个角 .5.异面直线所成的角的范围： .
6.异面直线所成角的求法:
2.“三个”推论推论1：经过一条直线和这条直线外一点，有且只有一个平面.推论2：经过两条 直线，有且只有一个平面.推论3：经过两条 直线，有且只有一个平面.
______________
____________________
___________________________
_______________________
常用结论1.垂直于同一条直线的两个平面 ，即若a⊥α，a⊥β，则 .2.平行于同一个平面的两个平面 ，即若α∥β，β∥γ，则 .3.垂直于同一个平面的两条直线 ，即若a⊥α，b⊥α，则 .4.若α∥β，a⊂α，则 .
常用结论1.垂直于同一条直线的两个平面平行，即若a⊥α，a⊥β，则α∥β.2.平行于同一个平面的两个平面平行，即若α∥β，β∥γ，则α∥γ.3.垂直于同一个平面的两条直线平行，即若a⊥α，b⊥α，则a∥b.4.若α∥β，a⊂α，则a∥β.
_____________________________
______________________
3.二面角(1)定义：从一条直线出发的 所组成的图形叫做二面角.(2)二面角的平面角：如图，在二面角α－l－β的棱l上任取一点O，以点O为垂足，在半平面α和β内分别作 的射线OA和OB，则射线OA和OB构成的∠AOB叫做二面角的平面角.
(3)二面角的范围： .
*常用结论1.三垂线定理平面内的一条直线如果和穿过这个平面的一条斜线在这个平面内的射影 ，那么它也和这条斜线 .2.三垂线定理的逆定理平面内的一条直线如果和穿过该平面的一条斜线垂直，那么它也和这条斜线在该平面内的射影 .3.两个相交平面同时垂直于第三个平面，它们的交线 于第三个平面.
3.二面角(1)定义：从一条直线出发的 所组成的图形叫做二面角.(2)二面角的平面角：如图，在二面角α－l－β的棱l上任取一点O，以点O为垂足，在半平面α和β内分别作 的射线OA和OB，则射线OA和OB构成的∠AOB叫做二面角的平面角.
*常用结论1.三垂线定理平面内的一条直线如果和穿过这个平面的一条斜线在这个平面内的射影垂直，那么它也和这条斜线垂直.2.三垂线定理的逆定理平面内的一条直线如果和穿过该平面的一条斜线垂直，那么它也和这条斜线在该平面内的射影垂直.3.两个相交平面同时垂直于第三个平面，它们的交线也垂直于第三个平面.
定理
性质
线面垂直的性质定理
1.空间向量基本定理如果三个向量a,b,c不共面,那么对任意一个空间向量p,存在唯一的有序实数组(x,y,z),使得p＝ .{a,b,c}叫做空间的一个基底.
2.空间位置关系的向量表示
1.若异面直线l1，l2所成的角为θ，其方向向量分别是u，v，则cs θ＝|cs|＝ .
2.直线AB与平面α相交于点B，设直线AB与平面α所成的角为θ，直线AB的方向向量为u,平面α的法向量为n,则sin θ＝|cs| ＝ .
3.若平面α,β的法向量分别是n1和n2,则平面α与平面β的夹角即为向量n1和n2的夹角或其补角.设平面α与平面β的夹角为θ,则cs θ＝|cs|＝ .
如图,已知平面α的法向量为n,A是平面α内的定点,P是平面α外一点.过点P作平面α的垂线l,交平面α于点Q,则n是直线l的方向向量,且点P到平面α的距离