甘肃省武威二十一中学教研片2024-2025学年八年级上学期期中质量检测数学试卷

这是一份甘肃省武威二十一中学教研片2024-2025学年八年级上学期期中质量检测数学试卷，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（每小题只有一个正确答案，每小题3分，共30分）
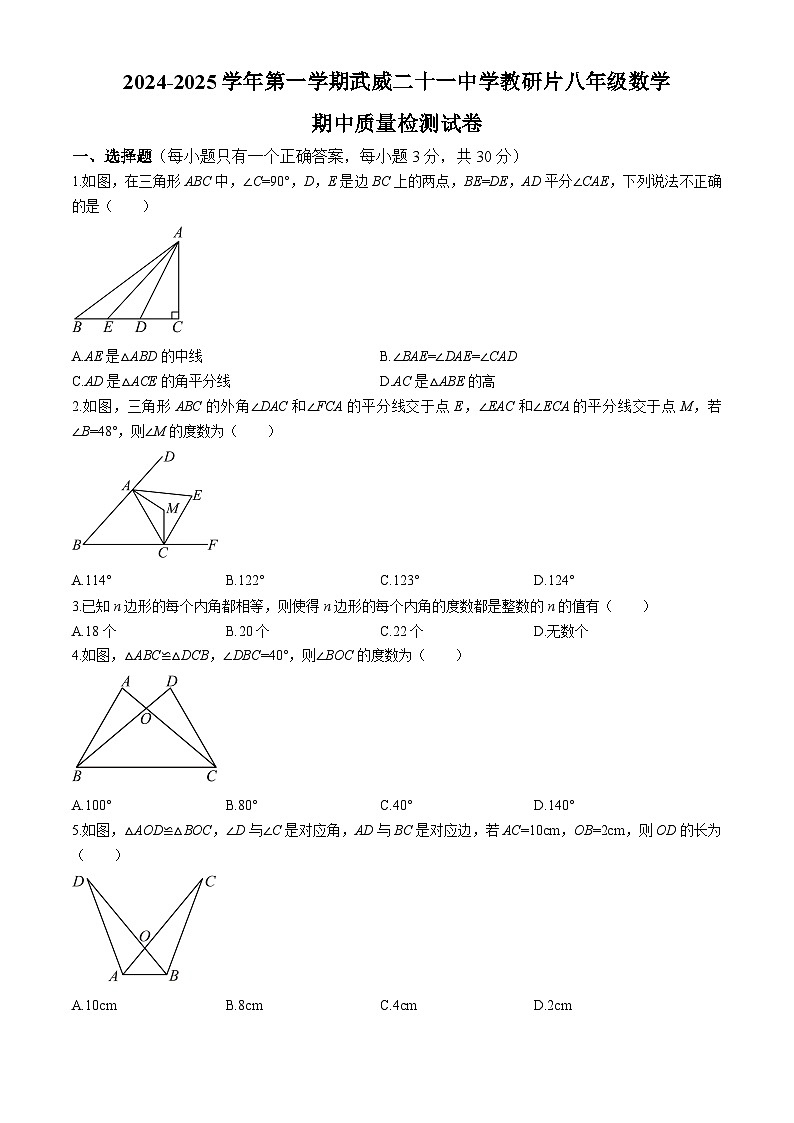
1.如图，在三角形ABC中，∠C=90°，D，E是边BC上的两点，BE=DE，AD平分∠CAE，下列说法不正确的是（ ）
A.AE是△ABD的中线B.∠BAE=∠DAE=∠CAD
C.AD是△ACE的角平分线D.AC是△ABE的高
2.如图，三角形ABC的外角∠DAC和∠FCA的平分线交于点E，∠EAC和∠ECA的平分线交于点M，若∠B=48°，则∠M的度数为（ ）
A.114°B.122°C.123°D.124°
3.已知n边形的每个内角都相等，则使得n边形的每个内角的度数都是整数的n的值有（ ）
A.18个B.20个C.22个D.无数个
4.如图，△ABC≌△DCB，∠DBC=40°，则∠BOC的度数为（ ）
A.100°B.80°C.40°D.140°
5.如图，△AOD≌△BOC，∠D与∠C是对应角，AD与BC是对应边，若AC=10cm，OB=2cm，则OD的长为（ ）
A.10cmB.8cmC.4cmD.2cm
6.如图，在三角形ABC和△DBE中，AC=DE，还需添加两个条件才能使△ABC≌△DBE，添加的一组条件不正确的是（ ）
A.AB=DB，BC=BEB.AB=DB，∠C=∠E
C.∠A=∠D，∠ABD=∠CBED.∠A=∠D，AB=DB
7.如图，∠ACB=90°，AC=BC.AD⊥CE，BE⊥CE，垂足分别是点D、E，AD=3，BE=1，则DE的长是（ ）
A.B.2C.D.
8.如图，AB∥CD，BP和CP分别平分∠ABC和∠DCB，AD过点P，且与AB垂直，若AD=8，则点P到BC的距离是（ ）
A.8B.6C.4D.2
9.在三角形内，到三角形三个顶点的距离都相等的点是这个三角形的（ ）
A.三条中线的交点B.三条高的交点C.三条角平分线的交点D.三条边的垂直平分线的交点
10.如图，在三角形ABC中，∠ACB=90°，AC=BC，AD平分∠BAC，CE⊥AD交AB于E，点G是AD上的一点，且∠ACG=45°，连BG交CE于P，连DP，下列结论：①AC=AE，②CD=BE，③BG+2DP=AD，④PG=PE，其中正确的有（ ）
A.①②③B.①②④C.①③④D.①②③④
二、填空题（每小题3分，共24分）
11.如图，CD是△ABC的中线，BE是△BCD的中线，△ABC的面积为10，则△BDE的面积为________.
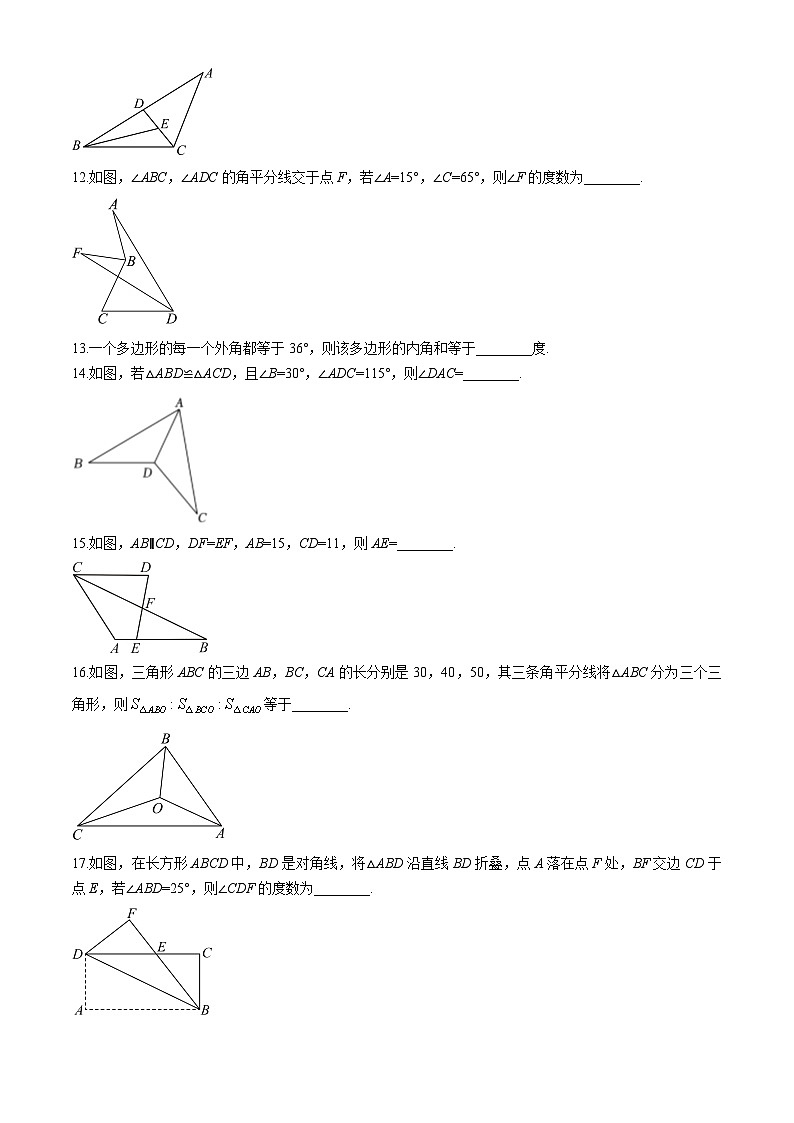
12.如图，∠ABC，∠ADC的角平分线交于点F，若∠A=15°，∠C=65°，则∠F的度数为________.
13.一个多边形的每一个外角都等于36°，则该多边形的内角和等于________度.
14.如图，若△ABD≌△ACD，且∠B=30°，∠ADC=115°，则∠DAC=________.
15.如图，AB∥CD，DF=EF，AB=15，CD=11，则AE=________.
16.如图，三角形ABC的三边AB，BC，CA的长分别是30，40，50，其三条角平分线将△ABC分为三个三角形，则等于________.
17.如图，在长方形ABCD中，BD是对角线，将△ABD沿直线BD折叠，点A落在点F处，BF交边CD于点E，若∠ABD=25°，则∠CDF的度数为________.
18.如图15，在Rt△ABC中，∠C=90°，BD平分∠ABC交AC于点D，过点D作DE∥BC交AB于点E，∠ABC=30°，DC=3.动点P从点B出发，沿着B→C→A运动，当时，则∠PEB的度数为________.
三、解答题（共66分）
19.（6分）如图16，在平面直角坐标系中，三角形ABC的三个顶点坐标分别是A（-2，-4），B（0，-4），C（2，-1）.
（1）请在图中作出关于x轴对称的图形；
（2）写出，，三点坐标；
（3）求的面积.
20.（6分）已知三角形的三边长分别为a、b、c，化简：.
21.（6分）如图，在三角形ABC中，BD为AC边上的中线，已知BC=8，AB=5，△BCD的周长为20，求△ABD的周长.
22.（6分）若一个n边形的内角和的比它的外角和少150°，求n的值.
23.（8分）如图，已知在三角形ABC、三角形ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C、D、E三点在同一直线上，连接BD.求证：△BAD≌△CAE.
24.（8分）如图，在四边形ABCD中，∠B=∠C=90°，点E在BC边上，DE平分∠ADC，∠AED=90°.
（1）求证：AE是∠DAB的平分线；
（2）求证：BE=CE.
25.（8分）如图，三角形ABC中，AD是∠BAC的角平分线，DE⊥AB于点E，DF⊥AC于点F，连接EF交AD于点G.
（1）求证：AD直平分EF；
（2）已知AB+AC=19，DE=2，求三角形ABC的面积.
26.（8分）如图，在等腰Rt△ABC中，∠ACB=90°，D为BC的中点，DE⊥AB，垂足为E，过点B作BF∥AC交DE的延长线于点F，连接CF.
（1）求证：AD⊥CF；
（2）连接AF，试判断△ACF的形状，并说明理由.
27.（10分）（1）（3分）如图1，△ABD，△AEC都是等边三角形.BE与CD交于点O，试猪想BE与CD之间的数量关系，并证明.

【深入研究】
（2）（3分）在（1）的条件下，证明OA平分∠DOE.
【探究应用】
（3）（4分）如图2，△AEC，△ABD都是等腰直角三形，∠BAD=∠CAE=90°，AD=AB，AC=AE连接BC，DE，点M是BC的中点，判断AM与DE之间的关系，并证明.
答案
1-5 BCCAB 6-10 BBCDC
11.2.5；12.25°；13.1440；14.35°；15.4；16.3：4：5；17.40；18.75°或150°
19.（1）如图所示：即为所求；
（2）由图可得，，，；（3）.
20.
21.的周长为17.
22.
23.，
，
即：，
在和中，
，
.
24.（1）过点作于点，则，
平分，
，
在和中，
，
，
，
，
，，
，
，
，
是的平分线；
（2）由（1）知：，
，
，
，
是的平分线，，，
，
.
25.（1）是的角平分线，于点，于点，
，
在和中，
，
，
，
又，
垂直平分；
（2）由（1）可知.
，，，
.
26.（1）三角形ABC是等腰直角三角形，
，，
，即，
，
，，
，
，
三角形BDF是等腰直角三角形，则，
点为的中点，
，
在，中，
，
，
，
，
，
，
；
（2）三角形ACF是等腰三角形，理由如下，
如图所示，连接，
由（1）可知，，三角形BDF是等腰直角三角形，，
，平分，点是的中点，即是的垂直平分线，
，
，
是等腰三角形.
27.（1），证明如下：
和都是等边三角形，
，，，
，
即.
在和中
，
，
；
（2）过点A分别作，，垂足为点，.
由（1）知：，
点A在的平分线上，
即平分；
（3），且，证明如下：
延长到，使，连接，延长交于，如图：
点是的中点，
，
，，
，
，，
，
，
，
，
，
，
，
，
，
，，
，
，
，
，
，
；