2023-2024学年福建省龙岩市永定区七年级（上）期末数学试卷

这是一份2023-2024学年福建省龙岩市永定区七年级（上）期末数学试卷，共10页。试卷主要包含了本试题分为第Ⅰ卷和第Ⅱ卷两部分，下列运算正确的是，若，则下列变形错误的是，若与是同类项，则的值为等内容，欢迎下载使用。

（答题时间：120分钟，满分：150分）
注意：1．本试题分为第Ⅰ卷和第Ⅱ卷两部分．
2．请把所有答案填涂或书写到答题卡上！在本试题上答题无效．
第Ⅰ卷
一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，
只有一项是符合题目要求的，把答案填涂在答题卡的相应位置．
1．2024的相反数是（ ）
A．2024B．C．D．
2．中国人民解放军海军福建舰（舷号：18，简称福建舰），是中国完全自主设计建
造的首艘弹射型航空母舰，采用平直通长飞行甲板，配置电磁弹射和阻拦装置，
满载排水量8万余吨．将数字8万用科学记数法表示为（ ）
A．B．C．D．
3．下列运算正确的是（ ）
A．B．
C．D．
4．若，则下列变形错误的是（ ）
A．B．
C．D．
5．若与是同类项，则的值为（ ）
A．B．C．D．
第6题图
①
②
③
④
6．如图，方格纸上每个小正方形的边长都相同，若剪掉一个
小正方形阴影部分能折叠成一个正方体，则剪掉的小正方
形不可以是（ ）
A．①B．②
C．③D．④
7．小咏用现金买了8支相同的签字笔，找回了（）元，有下列两种说法：
说法Ⅰ：若小咏原有现金50元，则每支签字笔元；
说法Ⅱ：若每支签字笔元，则小咏原有现金元．
则下面判断正确的是（ ）
A．Ⅰ对Ⅱ错B．Ⅰ错Ⅱ对C．Ⅰ与Ⅱ都对D．Ⅰ与Ⅱ都错
8．某网店店家为迎接“庆元旦·迎新春”促销活动，在A批发市场以每件元的价
格进了40件童装，又在B批发市场以每件元（）的价格进了同样的60件
童装．如果店家以每件元的价格卖出这款童装，卖完后，这家商店（ ）
A．盈利了B．亏损了C．不赢不亏D．盈亏不能确定
第9题图
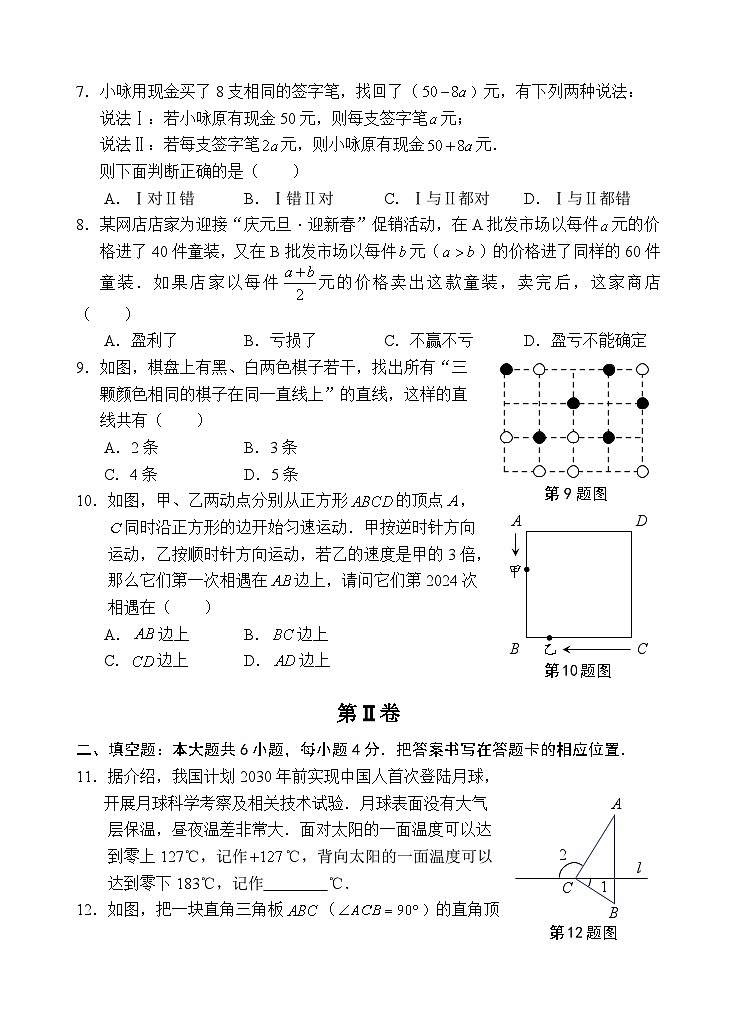
9．如图，棋盘上有黑、白两色棋子若干，找出所有“三
颗颜色相同的棋子在同一直线上”的直线，这样的直
线共有（ ）
A．2条B．3条
C．4条D．5条
甲
A
B
C
D
乙
第10题图
10．如图，甲、乙两动点分别从正方形的顶点，
同时沿正方形的边开始匀速运动．甲按逆时针方向
运动，乙按顺时针方向运动，若乙的速度是甲的3倍，
那么它们第一次相遇在边上，请问它们第2024次
相遇在（ ）
A．边上B．边上
C．边上D．边上
第Ⅱ卷
二、填空题：本大题共6小题，每小题4分．把答案书写在答题卡的相应位置．
11．据介绍，我国计划2030年前实现中国人首次登陆月球，
1
2
A
B
C
l
第12题图
开展月球科学考察及相关技术试验．月球表面没有大气
层保温，昼夜温差非常大．面对太阳的一面温度可以达
到零上127℃，记作℃，背向太阳的一面温度可以
达到零下183℃，记作 ℃．
12．如图，把一块直角三角板（）的直角顶
点放在直线上，若，则的度数为 ．
13．下列生活、生产现象：
①把弯曲的公路改直，就能缩短路程；
②用两颗钉子就可以把一根木条固定在墙上；
③从到铺设水管，总是尽可能沿线段铺设；
④植树时，只要栽下两棵树，就可以把同一行树栽在同一直线上．
可用“两点之间，线段最短”来解释的现象有 ．
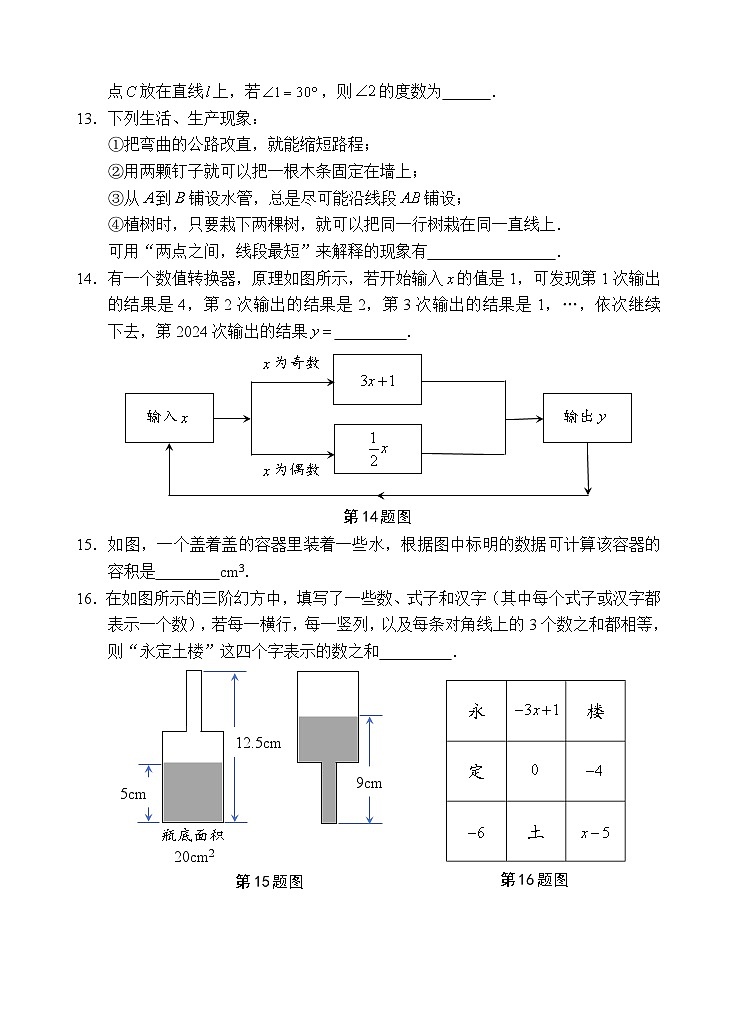
14．有一个数值转换器，原理如图所示，若开始输入的值是1，可发现第1次输出
的结果是4，第2次输出的结果是2，第3次输出的结果是1，…，依次继续
下去，第2024次输出的结果 ．
为奇数
输入
输出
为偶数
第14题图
15．如图，一个盖着盖的容器里装着一些水，根据图中标明的数据可计算该容器的
容积是 cm3．
16．在如图所示的三阶幻方中，填写了一些数、式子和汉字（其中每个式子或汉字都
表示一个数），若每一横行，每一竖列，以及每条对角线上的3个数之和都相等，
则“永定土楼”这四个字表示的数之和 ．
第15题图
9cm
5cm
瓶底面积20cm2
12.5cm
第16题图
永
定
土
楼
三、解答题：本大题共9小题，共86分．解答应写出文字说明、证明过程或演算步
骤．把答案书写在答题卡的相应位置．
17．（本题满分8分）
计算：．
18．（本题满分8分）
解方程：．
19．（本题满分8分）
先化简，再求值：，其中．
20．（本题满分8分）
我国古代名著《增删算法统宗》中有一题：“林下牧童闹如簇，不知人数不知竹．每人六竿多十四，每人八竿恰齐足．其大意是：“牧童们在树下拿着竹竿高兴的玩耍，不知有多少人和竹竿．每人6竿，多14竿；每人8竿，恰好用完．”请用列方程的方法求出这个问题中的牧童人数．
21．（本题满分8分）
如图，点是线段的中点，点为线段延长线上一点，且．
（1）用尺规作图将图形补充完整（保留作图痕迹，不写做法）；
（2）当时，求线段的长．
A
C
B
第21题图
22．（本题满分10分）
给出如下定义：我们把有序实数对（，，）叫做关于的二次多项式的附属系数对，把关于的二次多项式叫做有序实数对（，，）的附属多项式．
（1）关于的二次多项式的附属系数对为 ；
（2）有序实数对（，，）的附属多项式与有序实数对（，，）的附属多项式的差中不含二次项，求的值．
23．（本题满分10分）
已知关于的一元一次方程，其中为常数．
（1）若是该方程的解，求的值；
（2）若该方程的解为正整数，求满足条件的所有整数的值．
24．（本题满分12分）
在数学兴趣小组中，同学们从书上学到了很多有趣的数学知识．其中有一个数学知识引起了同学们的兴趣．根据，知道，可以求的值．如果知道，可以求的值吗？他们为此进行了研究，规定：若，那么（，）．例如：，则（3，27）．
（1）填空：（2，4） ，（4，64） ；
（2）计算：（，81）（5，125）；
（3）若（，）5，（4，）3，求（，）的值．
25．（本题满分14分）
将一副三角板（含有角的直角三角板和含有角的直角三角板）按如图-1摆放在直线上，平分，平分．
（1）求的度数；
（2）如图-2，将三角板绕着点以每秒的速度顺时针旋转，设旋转时间为秒（），平分．
①在旋转过程中，的度数是否发生改变？若不变，求出的度数，若改变，请说明理由；
②在旋转过程中，是否存在某个时刻，与中，其中一个角是另一个角的两倍？若存在，求出所有满足题意的值，若不存在，请说明理由．
N
F
C
D
B
A（E）
M
G
图-1
H
N
F
C
D
B
E
M
G
A
图-2
第25题图
永定区2023~2024学年度第一学期初中阶段期末质量监测
七年级数学参考答案
一、选择题（本大题共10小题，每小题4分，共40分）
二、填空题（本大题共6小题，每小题4分）
11． ﹣183 ． 12． 120° ． 13． ① ③ ．
14． 2 ． 15． 170 ． 16． 20 ．
三、解答题（本大题共9小题，共86分）
17．（8分）
解：原式
………………………………………………………………………… 6分
………………………………………………………………………… 8分

；
18．（8分）
………………………………………………………………… 2分
解：，
………………………………………………………………… 4分
，
………………………………………………………………… 6分
，
，
………………………………………………………………… 8分
．
19．（8分）
解：原式
…………………………………………………………………………… 5分
．
当时，
原式
…………………………………………………………………………… 8分
．
……………………………………………………… 1分
20．（8分）
……………………………………………………… 4分
解：设这个问题中的牧童人数为，根据题意，
得
A
C
B
第21题图
D
……………………………………………………… 7分
解得 ．
……………………………………………………… 8分
答：这个问题中的牧童人数为7．
21．（8分）
解：（1）图形补充完整如图所示；
……………………………… 4分
（2）因为点是线段的中点，
所以，，
因为，
所以，
…………………………………………………………… 8分
所以．
22．（10分）
…………………………………………………………… 3分
解：（1） （1，，3） ；
（2）依题意，
得
…………………………………………………………… 7分
．
…………………………………………………………… 9分
因为差中不含二次项，
所以，
…………………………………………………………… 10分
解得 ．
23．（10分）
解：（1）因为，
所以，
，

因为是该方程的解，
…………………………………………………………… 5分
所以，
解得 ；
（2）由（1）可知，
因为方程的解为正整数，的值为整数，
所以 ，
…………………………………………………………… 10分
或2或3或6，
解得 或0或1或4．
24．（12分）
………………………………………………………… 4分
解：（1） 2 ， 3 ．
（2）因为，
所以（，81），
因为，
所以（5，125），
………………………………………………………… 8分
所以原式．
（3）因为，
所以，
因为，
所以，
所以（，）（，64），
因为，
………………………………………………………… 12分
所以（，64）．
25．（14分）
N
F
C
D
B
A（E）
M
G
图-1
解：（1）由题意可知：，，
所以，，
因为平分，平分，
所以，
，
………………………………………… 4分
所以；
H
N
F
C
D
B
E
M
G
A
图-2
（2）①不变，理由如下：
由题意可知：，
所以
，

，
因为平分，平分，
所以，
，
所以

………………………………………… 8分

；
②由①可知：
H
N
F
C
D
B
E
M
G
A
图-2-1
，

，
1）当时（如图-2-1），
，解得，
H
N
F
C
D
B
E
M
G
A
图-2-2
2）当时（如图-2-2），
…………… 14分
，解得，
综上所述，满足题意的值为7或17．
题号
1
2
3
4
5
6
7
8
9
10
答案
B
C
D
C
A
D
C
A
B
D