2023-2024学年山东省临沂市罗庄区八年级下学期期末数学试题及答案

这是一份2023-2024学年山东省临沂市罗庄区八年级下学期期末数学试题及答案，共7页。试卷主要包含了8，9，代入得，1500；分，△PCF是等腰直角三角形．分等内容，欢迎下载使用。
2.答题时，端正心态，认真审题，认真书写，规范作图，保持卷面整洁！
一、选择题（本大题共10小题，每小题3分，共30分）
1．计算等于（ ）
A．B．2C．4D．
2．在同一平面直角坐标系中，和（k为常数，）的图象可能是（ ）
A． B． C． D．
3．如图，将一副直角三角板和一把宽度为1cm的直尺按如图方式摆放：先把和角
的顶点及它们的直角边重合，再将此直角边垂直于直尺的上沿，重合的顶点落在直尺下
沿上，这两个三角板的斜边分别交直尺上沿于A，B两点，则AB的长是（ ）
A．B．C．1D．
4．某位运动员在一次射击训练中，次射击的成绩如图，则这10次成绩的平均数和中
位数分别是（ ）
A．9.8，9.5B．9.8，9.6C．9.8，9.7D．9.7，9.8
5．已知，则的化简结果是（ ）
A．-1B．-3C．-1-2kD．2k-3
6．如图，矩形ABCD中，对角线BD的垂直平分线MN分别交AD，BC于点M，N．若
AM=2，BN=4，则BD的长为（ ）
第3题图
第4题图
第6题图
A．B．C．D．
7．如图，在正方形ABCD中，点E，F分别是AB，CD的中点，AF，DE相交于点M，
G为BC上一点，N为EG的中点．若BG=4，CG=1，则线段MN的长度为（ ）
A．B．C．2D．
8．如图，点A、B、C在同一条线上，点B在点A，C之间，点D，E在直线AC同侧，，∠A=∠C= 90，△EAB≌△BCD，连接DE，设AB=a，，BC=b，DE=c，给出下面三个结论：①；②；③；所有正确结论个数是（ ）
A．0个B．1个C．2个D．3个
第7题图
第8题图
9.折返跑是一种跑步的形式．如图，在一定距离的两个标志物①、②之间，从①开始，沿
直线跑至②处，用手碰到②后立即转身沿直线跑至①处，用手碰到①后继续转身跑至②
处，循环进行，全程无需绕过标志物．小华练习了一次的折返跑，用时在整
个过程中，他的速度大小v（）随时间t（）变化的图像可能是（ ）
A． B． C． D．
10.如图，在菱形ABCD中，∠C＝120°，M是AB的中点，N是对角线BD上一动点，设
DN长为x，线段MN与AN长度的和为y，图2是y关于x的函数图象，图象右端点F的坐标为，则图象最低点E的坐标为（ ）
A．B．C．D．
第10题图
第9题图
二、填空题（本题共6个小题，每小题3分，共18分）
11.（1）在函数中，自变量x的取值范围是
（2）如图，在正方形ABCD中，AB=12，点E，F分别在边BC，CD上，AE与BF相交于点P，若BE=CF=5，则BP的长为
（3）如图，菱形ABCD的边长为4，，对角线AC与BD交于点O，E为OB中点，F为AD中点，连接EF，则EF的长为
（4）如图，在△ABC中，∠C=90，AC=BC=5．P为边AB上一动点，作PD⊥BC于点D，PE⊥AC于点E，则的最小值为
（5）规定：如果两个函数的图象关于y轴对称，那么称这两个函数互为“Y函数”．已知一次函数，则它的“Y函数”解析式为
第11（2）题图
第11（3）题图
第11（4）题图
第11（6）题图
（6）如图，在平面直角坐标系中，直线l:y=x+2交x轴于点A，交y轴于点A1，点A2，A3，…在直线l上，点B1，B2，B3，…在x轴的正半轴上，若△A1OB1，△A2B1B2，△A3B2B3，…，依次均为等腰直角三角形，直角顶点都在x轴上，则第n个等腰直角三角形△AnBn-1Bn顶点An的横坐标为
三、解答题（本大题共7小题，共72分）
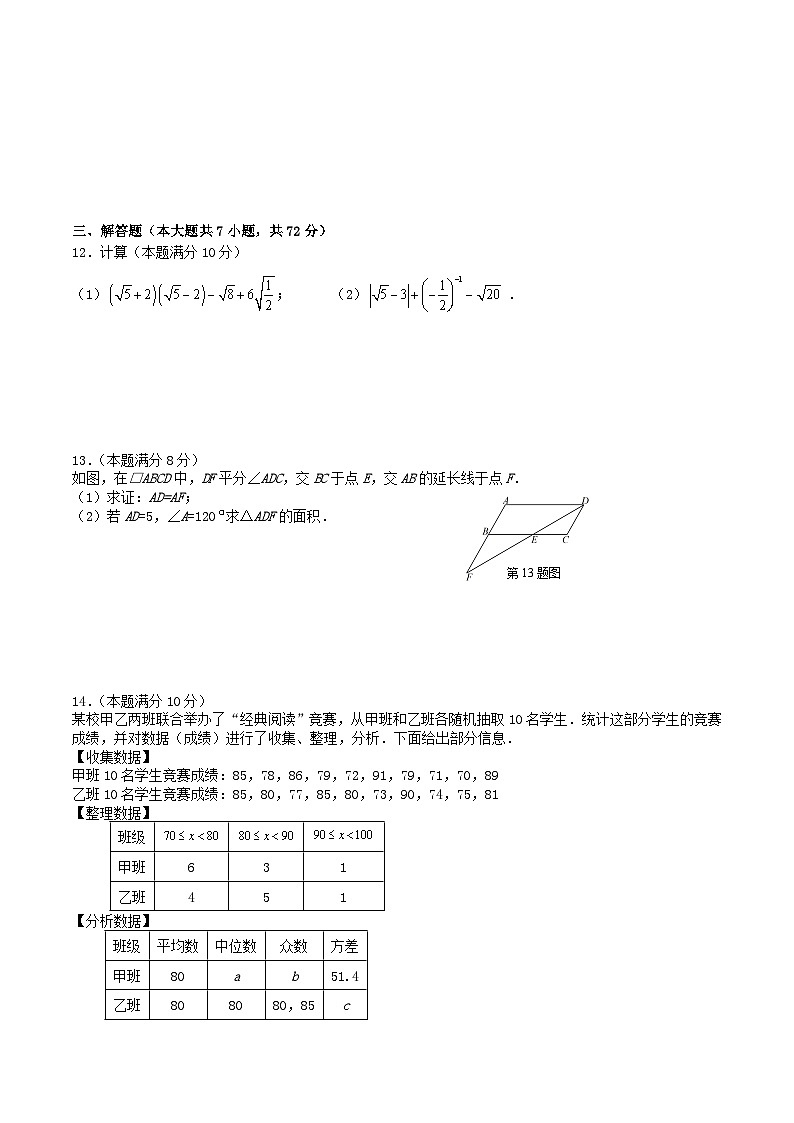
12．计算（本题满分10分）
（1）； （2） .
13．（本题满分8分）
如图，在□ABCD中，DF平分∠ADC，交BC于点E，交AB的延长线于点F．
（1）求证：AD=AF；
（2）若AD=5，∠A=120求△ADF的面积．
第13题图
14．（本题满分10分）
某校甲乙两班联合举办了“经典阅读”竞赛，从甲班和乙班各随机抽取10名学生．统计这部分学生的竞赛成绩，并对数据（成绩）进行了收集、整理，分析．下面给出部分信息．
【收集数据】
甲班10名学生竞赛成绩：85，78，86，79，72，91，79，71，70，89
乙班10名学生竞赛成绩：85，80，77，85，80，73，90，74，75，81
【整理数据】
【分析数据】
【解决问题】根据以上信息，回答下列问题：
（1）填空：_________，_________，_________；
（2）请你根据【分析数据】中的信息，判断哪个班成绩比较好，简要说明理由：
（3）甲班共有学生40人，乙班共有学生45人．按竞赛规定，80分及80分以上的学生可以获奖，估计这两个班可以获奖的总人数是多少？
15．（本题满分10分）
在平面直角坐标系中，函数y=kx+b（k≠0）的图象经过点A（0，1）和B（1，3），与过点（0，5）且平行于x轴的线交于点C．
（1）求该函数的解析式及点C的坐标；
（2）当时，对于x的每一个值，函数的值大于函数的值且小于5，请判断出n是个取值范围还是个确定的值，若n是个取值范围，直接写出n的取值范围，若n是个确定的值，直接写出n的值．
16.（本题满分10分）
如图，在□ABCD中，对角线AC与BD相交于点O，AC平分∠DAB，过点B作BE⊥AB交AC于点E．
（1）求证：AC⊥BD；
（2）若AB=5，AC =8，求OE的长．
第16题图
17．（本题满分12分）
临沂外卖市场竞争激烈，美团、饿了么等公司订单大量增加，某公司负责招聘外卖送餐员，方案如下：每月不超出750单，每单收入元；超出750单的部分每单收入m元．
（1）若某“外卖小哥”某月送了450单，收入 元；
（2）若“外卖小哥”每月收入为y（元），每月送单量为x单，y与x之间的关系如图所示，求y与x之间的函数关系式；
（3）若“外卖小哥”甲和乙在某个月内共送单1600单，且甲送单量低于乙送单量，共收入5920元，问：甲、乙送单量各是多少？
第17题图
18．（本题满分12分）
如图1，点P是线段AB上与点A，点B不重合的任意一点，在AB的同侧分别以A，P，B为顶点作，其中与的一边分别是射线AB和射线BA，的两边不在直线AB上，我们规定这三个角互为等联角，点P为等联点，线段AB为等联线．
如图2，在Rt△APC中，∠A =90，，延长AP至点B，使AB=AC，作∠A的等联角∠CPD和∠PBD．将△APC沿PC折叠，使点A落在点M处，得到△MPC，再延长PM交BD的延长线于E，连接CE并延长交PD的延长线于F，连接BF．
（1）确定△PCF的形状，并说明理由；小明通过研究发现，过点C作CN⊥BE交BE的延长线于点N，可以解决，请你帮小明完成说理；
（2）若，，求等联线AB的长；
（3）在（2）的条件下，求线段PE的长.
（注意：本题分步给分，若第一问做不出，可用第一问的结论做二三问，同样给分）
备用图
第18题图
图2
图1
参考答案
一、选择题（本大题共10小题，每小题3分，共30分）
二、填空题（本题共6个小题，每小题3分，共18分）
11（1）且 （2） （3） （4） （5） （6）
三、解答题（本大题共7小题，共72分）
12．（本题满分10分）解：（1）原式 …（5分）
（2）原式 …（10分）
13．（本题满分8分）（1）证明：在□ABCD中，AB∥CD，∴，∵平分，∴，∴，∴．分
（2）解：过D作交的延长线于H，∵∠A=120, AD=AF=5，∴，∴，∴，∴，
∴的面积．分
14．（本题满分10分）（1）分,分,分;
（2）乙班成绩比较好分理由：乙班成绩与甲班平均数相同，中位数、众数高于甲班，方差小于甲班，总体乙班成绩比较好．分（一条理由即可）
（3）获奖人数：（人）．答：获奖人数为43人．分
15.（本题满分10分）（1）解：把点A（0，1），B（1，3）代入得：，解得：，∴该函数的解析式为，分
由题意知点C的纵坐标为5，当时，解得：，∴C（2，5）；分
（2）．分
16．（本题满分10分）（1）证明：∵AC平分∠DAB，∴∠DAC=∠BAC, ∵四边形是平行四边形，∴AD∥CB , ∴∠DAC=∠ACB ∴∠CAB=∠ACB ∴AB=CB，∴四边形是菱形，∴AC⊥BD．分
（2）解：四边形是平行四边形，，，，
，，分
设OE=x，则解得： ∴分
17.（本题满分12分）（1）1500；分
（2）当0≤x≤750时，y＝x,当x＝750时，y＝分
当x>750时，设y＝kx+b，根据题意得，解得，
∴y＝6x﹣2000,综上：分（不合在一起不扣分）
（3）750×2=1500750时，则6a-2000+6（1600﹣a）-2000＝5600≠5920，不合题意，分;当0