

辽宁省大连市金普新区2024-2025学年九年级上学期期中考试数学试卷
展开
这是一份辽宁省大连市金普新区2024-2025学年九年级上学期期中考试数学试卷,共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
1.(3分)下列方程中,是关于x的一元二次方程的是( )
A.3x﹣1=0B.x+2y=3C.x2+2x﹣1=0D.x4﹣1=0
2.(3分)在平面直角坐标系中,点(1,3)关于原点对称的点的坐标是( )
A.(﹣1,﹣3)B.(﹣1,3)C.(1,﹣3)D.(3,1)
3.(3分)下面用数学家名字命名的图形中,既是轴对称图形,又是中心对称图形的是( )
A. 赵爽弦图B. 笛卡尔心形线
C. 科克曲线D. 斐波那契螺旋线
4.(3分)已知⊙O的半径为5,点P在⊙O外,则OP的长可能是( )
A.3B.4C.5D.6
5.(3分)若关于x的一元二次方程x2﹣2x+k=0有两个不相等的实数根,则k的值可以是( )
A.﹣1B.1C.2D.3
6.(3分)“读万卷书,行万里路.”某校为了丰富学生的阅历知识,坚持开展课外阅读活动,学生人均阅读量从七年级的每年100万字增加到九年级的每年121万字.设该校七至九年级人均阅读量年均增长率为x,则可列方程为( )
A.100(1+x)2=121
B.100(1+x%)2=121
C.100(1+2x)=121
D.100+100(1+x)+100(1+x)2=121
7.(3分)如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,若⊙O的半径为13,CD=24,则AE的长为( )
A.5B.6C.7D.8
8.(3分)二次函数y=2x2+bx+1的图象关于直线对称,且经过点(1,k),则k的值为( )
A.3B.﹣3C.6D.﹣6
9.(3分)如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=4,将△CAB绕点C按逆时针方向旋转得到△CDE,点D恰好在AB边上,连接BE,则BE的长为( )
A.8B.C.D.6
10.(3分)如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点A出发以1cm/s的速度向点B运动,点Q从点B出发以2cm/s的速度向点C运动,设经过的时间为xs,△PBQ的面积为ycm2,则下列图象能反映y与x之间的函数关系的是( )
A.B.
C.D.
二、填空题(本题共5小题,每小题3分,共15分)
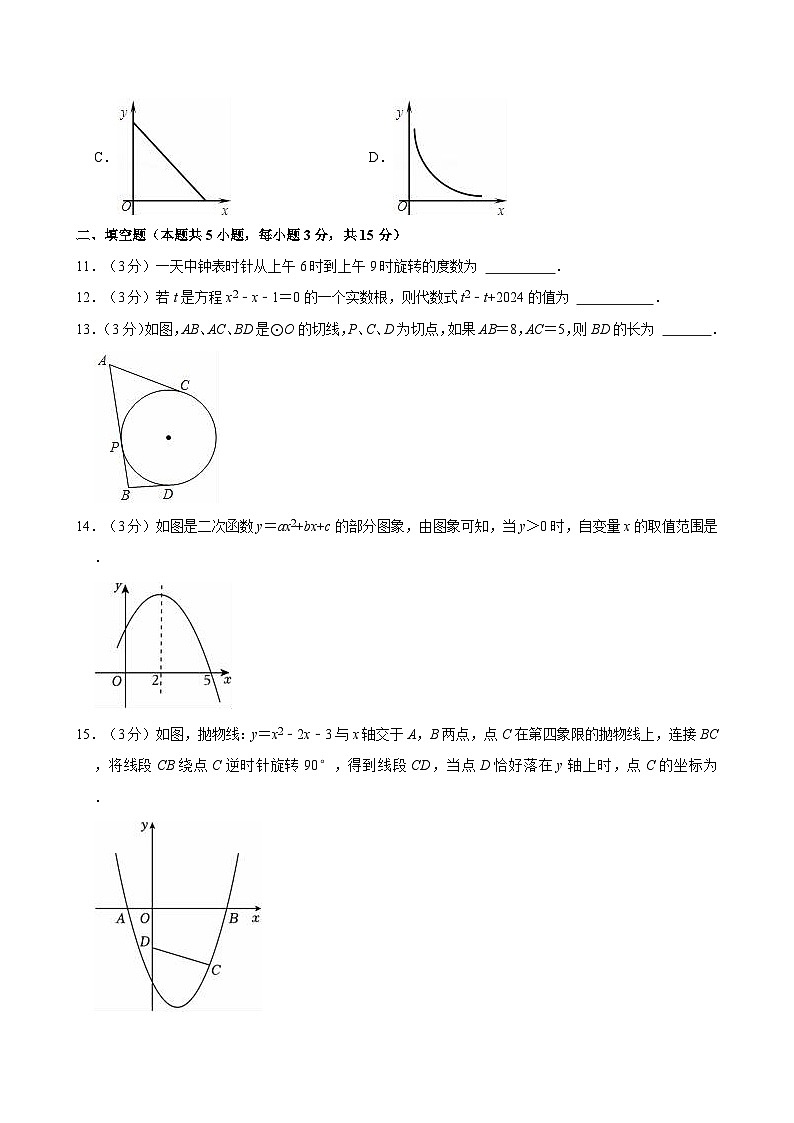
11.(3分)一天中钟表时针从上午6时到上午9时旋转的度数为 .
12.(3分)若t是方程x2﹣x﹣1=0的一个实数根,则代数式t2﹣t+2024的值为 .
13.(3分)如图,AB、AC、BD是⊙O的切线,P、C、D为切点,如果AB=8,AC=5,则BD的长为 .
14.(3分)如图是二次函数y=ax2+bx+c的部分图象,由图象可知,当y>0时,自变量x的取值范围是 .
15.(3分)如图,抛物线:y=x2﹣2x﹣3与x轴交于A,B两点,点C在第四象限的抛物线上,连接BC,将线段CB绕点C逆时针旋转90°,得到线段CD,当点D恰好落在y轴上时,点C的坐标为 .
三、解答题(本题共8小题,共75分.解答应写出文字说明,演算步骤或推理过程)
16.(10分)(1)用配方法解方程:x2﹣6x=﹣9;
(2)用公式法解方程:2x2+3x﹣4=0.
17.(8分)如图所示,在正方形网格中,△ABC的顶点均在格点上,请在所给平面直角坐标系中按要求作图.
(1)以A点为旋转中心,将△ABC绕点A顺时针旋转90°得△AB1C1,画出△AB1C1,并写出B1,C1的坐标:
(2)直接写出线段BC与B1C1的关系: .
18.(8分)如图,已知四边形ABCD是⊙O的内接四边形,延长DC,AB相交于点E,且∠ABC=2∠E.求证:△ADE是等腰三角形.
19.(8分)如图,矩形画框由边框和内衬组成,其中画框的边框宽度相等,画框外框长为32cm,宽为20cm,且边框的面积为整个画框面积的,求这个矩形画框的边框宽度是多少厘米?
20.(8分)某商场以每件20元的价格购进一种商品,规定这种商品每件售价不低于进价,又不高于36元,经市场调查发现:该商品每天的销售量y(件)与每件售价x(元)之间符合一次函数关系,如图所示.
(1)求y与x之间的函数关系式,并直接写出自变量x的取值范围;
(2)设商场销售这种商品每天获利w(元),当每件商品的售价定为多少元时,每天销售利润最大?最大利润是多少?
21.(8分)如图1,AB是⊙O的直径,AC是弦,D是的中点,CD与AB交于点E,点F在AB延长线上,且CF=EF.
(1)求证:CF为⊙O的切线;
(2)如图2,连接BD,若CF=8,BF=4,求BD的长.
22.(12分)如图1,在△ABC中,AC=BC,∠ACB=90°,点D是线段AB上一点(不与点A,B重合),∠ACD=α(0°<α<45°),以D为旋转中心,将线段DC顺时针旋转90°得到线段DE,连接EB.
(1)求∠EDB(用含α的式子表示);
(2)求证;BE⊥CB;
(3)如图2,当AD=2,时,求△BCD的面积.
23.(13分)已知y1是自变量x的函数,当y2=xy1+3时,称函数y2为函数y1的“相关函数”.
例如:函数y1=2x,当时,则函数是函数y1=2x的“相关函数”.
(1)点A(m,n)在函数y1=3x的图象上,判断点B(m,mn+3)是否在函数y1的“相关函数”y2的图象上,并说明理由;
(2)函数y1=﹣x+2的“相关函数”为y2,y1与y2的图象交于A,B两点,点A在点B的左侧,y2的图象与y轴交于点C,点P在y2的图象上,其横坐标为t.
①当点P在第一象限时,过点P作PQ⊥AB,垂足为点Q,当t为何值时,线段PQ的长度最大?最大值是多少?
②当t>0时,在y2的图象上,点C与点P之间部分(含点C和点P)的最大值与最小值之差为h,求h关于t的函数解析式,并直接写出自变量t的取值范围;
③在②的条件下,函数h图象上的点到直线h=4的距离为时,直接写出自变量t的值.
2024-2025学年辽宁省大连市金普新区九年级(上)期中数学试卷
参考答案与试题解析
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.【分析】根据一元二次方程的定义逐个判断即可.
【解答】解:A.3x﹣1=0,是一元一次方程,故本选项不符合题意;
B.x+2y=3,是二元一次方程,故本选项不符合题意;
C.x2+2x﹣1=0,是一元二次方程,故本选项符合题意;
D.x4﹣1=0,是一元四次方程,故本选项不符合题意.
故选:C.
【点评】本题考查了一元二次方程的定义,能熟记一元二次方程的定义(只含有一个未知数,并且所含未知数的项的最高次数是2的整式方程叫一元二次方程)是解此题的关键.
2.【分析】直接利用关于原点对称点的性质得出答案.
【解答】解:点A(1,3)关于原点O对称的点A1的坐标是:(﹣1,﹣3).
故选:A.
【点评】此题主要考查了关于原点对称点的性质,正确记忆横纵坐标关系是解题关键.
3.【分析】根据轴对称图形和中心对称图形的定义即可作答.
【解答】解:A.是中心对称,但不是轴对称;不符合题意;
B.是轴对称,但不是中心对称;不符合题意;
C.既是轴对称,也是中心对称;符合题意;
D.既不是轴对称,也不是中心对称;不符合题意;
故选:C.
【点评】本题主要考查了轴对称图形和中心对称图形的定义,熟练地掌握定义并能够区分轴对称图形和中心对称图形是解题的关键.
4.【分析】根据题意可以求得OP的取值范围,从而可以解答本题.
【解答】解:∵O的半径为5,点P在⊙O外,
∴OP>5,
故选:D.
【点评】本题考查点和圆的位置关系,解答本题的关键是明确题意,求出OP的取值范围.
5.【分析】根据方程的系数结合根的判别式Δ>0,可得出关于k的一元一次不等式,解之即可得出k的取值范围,对照四个选项即可得出结论.
【解答】解:∵关于x的一元二次方程x2﹣2x+k=0有两个不相等的实数根,
∴Δ=(﹣2)2﹣4×1×k=4﹣4k>0,
解得:k<1,故A正确.
故选:A.
【点评】本题主要考查了根的判别式,解题的关键是牢记“当Δ>0时,方程有两个不相等的实数根”.
6.【分析】增长率问题,一般用增长后的量=增长前的量×(1+增长率),如果设该校七至九年级人均阅读量年均增长率为x,根据题意即可列出方程求解.
【解答】解:设该校七至九年级人均阅读量年均增长率为x,
根据题意得100(1+x)2=121.
故选:A.
【点评】本题考查了一元二次方程的应用,掌握为增长率问题的一般形式为a(1+x)2=b,a为起始时间的有关数量,b为终止时间的有关数量是解决问题的关键.
7.【分析】连接OC,先根据垂径定理得出CE的长,再由勾股定理得出OE的长,进而可得出结论.
【解答】解:连接OC,
∵AB为⊙O的直径,弦CD⊥AB,垂足为点E,CD=24,
∴CE=CD=12,
∵⊙O的半径为13,
∴OE===5,
∴AE=OA﹣OE=13﹣5=8.
故选:D.
【点评】本题考查的是垂径定理和勾股定理,根据题意作出辅助线,构造出直角三角形是解题的关键.
8.【分析】先根据题意可得该二次函数的对称轴为直线,则由对称轴计算公式可得b=﹣6,据此得到二次函数解析式,再把(1,k)代入解析式中求解即可.
【解答】解:∵二次函数y=2x2+bx+1的图象关于直线对称,
∴该二次函数的对称轴为直线,
∴,
∴b=﹣6,
∴二次函数解析式为y=2x2﹣6x+1,
把(1,k)代入y=2x2﹣6x+1中得:k=2×12﹣6×1+1=﹣3,
故选:B.
【点评】本题主要考查了二次函数的性质,二次函数 图象上点的坐标特征,二次函数图象与几何变换,关键是二次函数性质的熟练应用.
9.【分析】由旋转的性质,可证△ACD、△BCE都是等边三角形,再根据含30度角的直角三角形的性质求出AB,由勾股定理求出BC的长,即可得到BE.
【解答】解:将△ABC绕点C按逆时针方向旋转得到△CDE,
则∠BCE=∠ACD,CB=CE,CA=CD,
∵∠A=60°,∠ACB=90°,
∴△ACD是等边三角形,∠ABC=30°,
∴∠ACD=60°,
∴∠BCE=60°,
∴△BCE是等边三角形,
∴BE=BC,
在Rt△ABC中,∠ABC=30°,
则AB=2AC=8,
∴,
∴,
故选:C.
【点评】本题主要考查了旋转的性质,等边三角形的判定与性质,含30度角的直角三角形,勾股定理,熟练掌握旋转的性质,证明等边三角形是解题的关键.
10.【分析】本题应读懂题意,写出函数解析式,根据实际问题列出函数关系式后判断函数的图象即可.
【解答】解:当Q在BC上时,△PBQ的面积为(4﹣x)×2x=4x﹣x2;函数图象为开口向下的二次函数,排除B,C、D.
故选:A.
【点评】本题考查了动点问题的函数图象,根据实际情况采用排除法求解.
二、填空题(本题共5小题,每小题3分,共15分)
11.【分析】钟表上的刻度把一个圆平均分成12等份,根据题意知,时针运行了圆周,即可得到答案.
【解答】解:根据题意,从上午6时到上午9时,共3个小时,
∴时针旋转了圆周,旋转的角度为.
故答案为:90°.
【点评】本题考查了钟表上角的认识的问题,知道钟表上的刻度把一个圆平均分成12等份是解题的关键.
12.【分析】先根据一元二次方程解的定义得到t2﹣t=1,然后利用整体代入的方法计算代数式的值.
【解答】解:∵t是方程x2﹣x﹣1=0的一个实数根,
∴t2﹣t﹣1=0,
∴原式=1+2024=2025.
故答案为:2025.
【点评】本题考查了解一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.
13.【分析】由AB、AC、BD是⊙O的切线,则AC=AP,BP=BD,求出BP的长即可求出BD的长.
【解答】解:∵AC、AP为⊙O的切线,
∴AC=AP,
∵BP、BD为⊙O的切线,
∴BP=BD,
∴BD=PB=AB﹣AP=8﹣5=3.
故答案为:3.
【点评】本题考查了切线长定理,两次运用切线长定理并利用等式的性质是解题的关键.
14.【分析】先求出抛物线与x轴的交点坐标,根据图象即可解决问题.
【解答】解:由图象可知,抛物线与x轴的交点坐标分别为(﹣1,0)和(5,0),
∴y>0时,x的取值范围为﹣1<x<5.
故答案为:﹣1<x<5.
【点评】本题考查抛物线与x轴的交点,对称轴等知识,解题的关键是学会根据图象确定自变量的取值范围.
15.【分析】证明△CND≌△BMC(AAS),则BM=CN,即﹣(﹣m2+2m+3)=m,即可求解.
【解答】解:过点C作x轴的平行线交过点B和y轴的平行线于点M,交y轴于点N,
设点C(m,m2﹣2m﹣3),
由题意得,CD=BC,∠BCD=90°,
则∠BCM+∠DCN=90°,∠DCN+∠CDN=90°,
∴∠BCM=∠CDN,
∵∠CND=∠BMC=90°,
∴△CND≌△BMC(AAS),
则BM=CN,即﹣(m2﹣2m﹣3)=m,
解得:m=(舍去负值),
则点C(,﹣),
故答案为:(,﹣).
【点评】本题考查的是抛物线与x轴的交点,全等三角形的判定与性质,熟练的利用方程思想解题是关键.
三、解答题(本题共8小题,共75分.解答应写出文字说明,演算步骤或推理过程)
16.【分析】(1)配方,开方,即可得出两个一元一次方程,求出方程的解即可;
(2)求出b2﹣4ac的值,再代入公式求出即可.
【解答】解:(1)x2﹣6x=﹣9,
x2﹣6x+9=﹣9+9,即(x﹣3)2=0,
∴x﹣3=0,
∴x1=x2=3;
(2)2x2+3x﹣4=0,
∵a=2,b=3,c=﹣4,
∴b2﹣4ac=32﹣4×2×(﹣4)=41>0,
∴x==,
∴x1=,x2=.
【点评】本题考查了解一元二次方程,能选择适当的方法解方程是解此题的关键.
17.【分析】(1)将点B、C绕点A顺时针旋转90°得其对应点,再首尾顺次连接即可得出答案;
(2)根据旋转的性质,结合图形可得答案.
【解答】解:(1)如图所示,△AB1C1即为所求.
由图知,B1的坐标为(﹣3,1),C1的坐标为(﹣2,3);
(2)结合图形知,BC⊥B1C1,且BC=B1C1,
故答案为:BC⊥B1C1,且BC=B1C1.
【点评】本题主要考查作图—旋转变换,解题的关键是掌握旋转变换的定义与性质.
18.【分析】根据圆内接四边形的性质和等腰三角形的判定定理证明.
【解答】证明:∵四边形ABCD是⊙O的内接四边形,
∴∠A=∠BCE,
∵∠ABC=2∠E,∠ABC=∠E+∠BCE,
∴∠BCE=∠BEC,
∴∠A=∠BEC,
∴DA=DE,
即△ADE是等腰三角形.
【点评】本题考查的是圆内接四边形的性质、等腰直角三角形的判定,掌握圆内接四边形的任意一个外角等于它的内对角是解题的关键,解答时,注意方程思想的灵活运用.
19.【分析】设这个矩形画框的边框宽度是x厘米,根据边框的面积为整个画框面积的,列出一元二次方程,解之取符合题意的值即可.
【解答】解:设这个矩形画框的边框宽度是x厘米,
由题意得:(32﹣2x)(20﹣2x)=(1﹣)×32×20,
整理得:x2﹣26x+48=0,
解得:x1=2,x2=24(不符合题意,舍去),
答:这个矩形画框的边框宽度是2厘米.
【点评】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
20.【分析】(1)设y与x之间的函数关系式为y=kx+b(k≠0),利用待定系数法即可求解;
(2)根据题意得w=﹣2(x﹣40)2+800,进而可得抛物线的对称轴为直线x=40,且开口向下,则当x<40时,y随x的增大而增大,当x=36时,w有最大值,代入函数即可求解.
【解答】解:(1)设y与x之间的函数关系式为y=kx+b(k≠0),
由所给函数图象可知:,
解得:,
∴y与x之间的函数关系式为y=﹣2x+120;
(2)∵y=﹣2x+120,
∴w=(x﹣20)y=(x﹣20)(﹣2x+120)=﹣2(x﹣40)2+800,
∴抛物线的对称轴为直线x=40,且开口向下,
∴当x<40时,y随x的增大而增大,
∵x≤36,
∴当x=36时,w有最大值,最大值为,
∴售价定38元/件时,每天最大利润为768元.
【点评】本题考查了一元二次方程的应用、二次函数的应用,理清题意,能从图象中获取相关信息来解决问题是解题的关键.
21.【分析】(1)根据垂径定理,等腰三角形的性质以及切线的判定方法进行解答即可;
(2)根据切割线定理可得FC2=FB•FA,依据切割线定理求出直径AB,再根据等腰直角三角形的性质进行计算即可.
【解答】(1)证明:如图1,连接OC,OD,
∵D是的中点,
∴=,
∴OD⊥AB,
∴∠ODE+∠OED=90°,
∵BC=BE,
∴∠BCE=∠BEC,
∵∠BEC=∠OED,
∴∠OCE+∠BCE=90°,
即OC⊥BC,
∵OC是⊙O的半径,
∴FC是⊙O的切线;
(2)解:如图2,连接BC,
∵CF是切线,FBA是割线,
∴FC2=FB•FA,
设直径AB为y,由64=4×FA,
解得AF=16,
∴AB=AF﹣FB=16﹣4=12,
连接AD,BD,
∵D是的中点,
∴=,
∴AD=BD,
∵AB是O的直径,
∴∠ADB=90°,
在Rt△ABD中,AD=BD,AB=12,
∴BD=AB=6.
【点评】本题考查切线的判定,圆周角定理,垂径定理,掌握垂径定理,圆周角定理以及切线的判定方法是正确解答的关键.
22.【分析】(1)由等腰直角三角形的性质得∠A=∠ABC=45°,再由三角形的外角性质得∠CDB=∠A+∠ACD=45°+α,即可得出结论;
(2)过点D作DM⊥AB,交AC于点F,交BC的延长线于点M,证明∠M=∠MBD=45°.得DM=DB.再证明△DCM≌△DEB(SAS),得∠M=∠DBE,则可得出答案;
(3)过点C作CH⊥BD于点H,设DH=x,则AH=CH=2+x,由勾股定理得出,求出x=1,求出BD和CH的长,则可得出答案.
【解答】(1)解:∵AC=BC,∠ACB=90°,
∴∠A=∠ABC=45°,
∴∠CDB=∠A+∠ACD=45°+α,
∵∠CDE=90°,
∴∠EDB=∠CDE﹣∠CDB=45°﹣α;
(2)证明:过点D作DM⊥AB,交AC于点F,交BC的延长线于点M,
则∠MDB=∠CDE=90°,
∴∠MDB﹣∠BDC=∠CDE﹣∠BDC,
即∠CDM=∠EDB,
∵∠MBD=45°,
∴∠M=∠MBD=45°,
∴DM=DB,
由旋转的性质得:DC=DE,
∴△DCM≌△DEB(SAS),
∴∠M=∠DBE=45°,
∴∠EBM=45°+45°=90°,
∴BE⊥BC;
(3)解:过点C作CH⊥BD于点H,
设DH=x,则AH=CH=2+x,
∵DH2+CH2=CD2,
∴,
∴x1=1,x2=﹣3(舍),
∴DH=1,CH=3,
∴BD=DH+BH=4,
∴=6.
【点评】本题是三角形综合题,考查了等腰直角三角形的性质,旋转的性质,全等三角形的判定和性质,勾股定理等知识点,熟练掌握相关知识点,添加辅助线,构造全等三角形是解题的关键.
23.【分析】(1)由新定义即可求解;
(2)由PQ=PH,即可求解;
②当0<t<1时,则在顶点处取得最大值4,在点C处取得最小值3,则h=4﹣3=1;当t≥1时,则抛物线的最小值为:﹣t2+2t+3,最大值为4,即可求解;
③显然此时,t>1,即|t2﹣2t+1﹣4|=,即可求解.
【解答】解:(1)点B(m,mn+3)在函数y1的“相关函数”y2的图象上,理由:
点A(m,n)在函数y1=3x的图象上,则n=3m,
由题意得,y2=xy1+3=x•3x+3,
当x=m时,y2=3m2+3=3m•m+3=mn+3,
即点B(m,mn+3)在函数y1的“相关函数”y2的图象上;
(2)由题意得,y2=xy1+3=﹣x2+2x+3,函数的大致图象如下:
①设点P(t,﹣t2+2t+3),过点P作PH∥y轴交AB于点H,则点H(t,﹣t+2),
由直线AB的表达式知,直线AB和x轴夹角为45°,
则PQ=PH=(﹣t2+2t+3+t﹣2)=(﹣t2+3t+1),
∵,
故PQ有最大值,
当t=时,PQ的最大值为:;
②由抛物线的表达式知,其对称轴为直线x=1,则顶点坐标为:(1,4),
当0<t<1时,则在顶点处取得最大值4,在点C处取得最小值3,
则h=4﹣3=1;
当t≥1时,
则抛物线的最小值为:﹣t2+2t+3,最大值为4,
即h=4﹣(﹣t2+2t+3)=t2﹣2t+1,
综上,h=;
③函数h的图象如下:
显然此时,t>1,
即|t2﹣2t+1﹣4|=,
解得:t=1+或1+(不合题意的值已舍去).
【点评】本题考查的是一次函数综合运用,涉及到二次函数的图象和性质,理解新定义和数形结合是解题的关键.
相关试卷
这是一份辽宁省大连市金普新区2024-2025学年九年级上学期10月月考数学卷,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份辽宁省大连市金普新区2023-2024学年八年级上学期期中数学试卷,共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份辽宁省大连市金普新区2023-2024学年九年级上学期期中数学试题,共13页。试卷主要包含了11等内容,欢迎下载使用。










