浙江省宁波市余姚市子陵教育集团2024-2025学年八年级上学期期中数学试卷

这是一份浙江省宁波市余姚市子陵教育集团2024-2025学年八年级上学期期中数学试卷，共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（3分）下面四个图形分别是节能、节水、低碳和绿色食品标志，在这四个标志中，是轴对称图形的是（ ）
A．B．C．D．
2．（3分）若a＜b，则下列不等式中成立的是（ ）
A．a﹣3＞b﹣3B．a+3＞b+3C．﹣3a＞﹣3bD．
3．（3分）等腰三角形的底角等于50°，则这个等腰三角形顶角的度数是（ ）
A．50°B．65°C．80°D．100°
4．（3分）如图，点E、H、G、N共线，∠E＝∠N，EF＝NM，添加一个条件，不能判断△EFG≌△NMH的是（ ）
A．EH＝NGB．∠F＝∠MC．FG＝MHD．FG∥HM
5．（3分）如图，△ABC中，D为AB中点，E在AC上，且BE⊥AC．若DE＝5，AE＝8，则BE的长度是（ ）
A．5B．5.5C．6D．6.5
6．（3分）给出下列命题：①三角形任何两边之和大于第三边；②三角形任何一外角等于两内角之和；③两边和一角对应相等的两个三角形全等，下列属于真命题的是（ ）
A．①③B．②③C．①②D．①
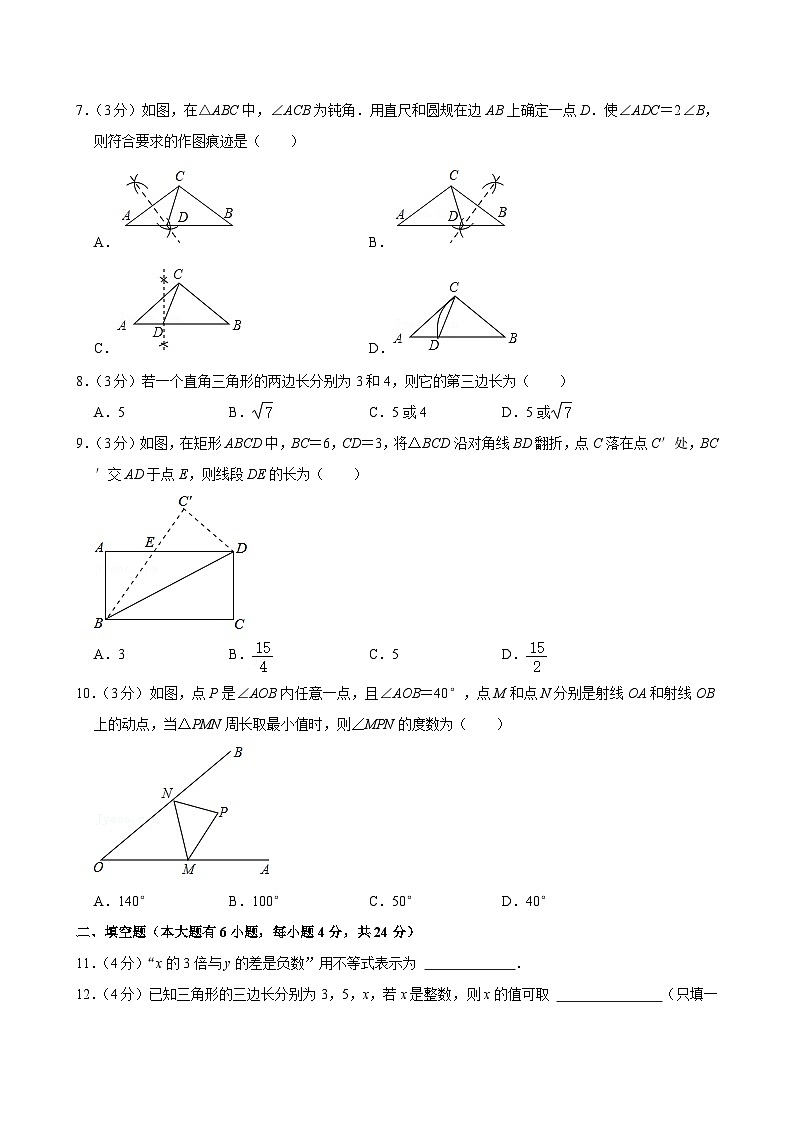
7．（3分）如图，在△ABC中，∠ACB为钝角．用直尺和圆规在边AB上确定一点D．使∠ADC＝2∠B，则符合要求的作图痕迹是（ ）
A．B．
C．D．
8．（3分）若一个直角三角形的两边长分别为3和4，则它的第三边长为（ ）
A．5B．C．5或4D．5或
9．（3分）如图，在矩形ABCD中，BC＝6，CD＝3，将△BCD沿对角线BD翻折，点C落在点C′处，BC′交AD于点E，则线段DE的长为（ ）
A．3B．C．5D．
10．（3分）如图，点P是∠AOB内任意一点，且∠AOB＝40°，点M和点N分别是射线OA和射线OB上的动点，当△PMN周长取最小值时，则∠MPN的度数为（ ）
A．140°B．100°C．50°D．40°
二、填空题（本大题有6小题，每小题4分，共24分）
11．（4分）“x的3倍与y的差是负数”用不等式表示为 ．
12．（4分）已知三角形的三边长分别为3，5，x，若x是整数，则x的值可取 （只填一个）．
13．（4分）“内错角相等，两直线平行”的逆命题是 ．
14．（4分）在△ABC中，∠A，∠B，∠C的对边分别是a，b，c，且满足（a﹣b）2+|b﹣c|2＝0，则△ABC是 三角形．
15．（4分）如图，△ABC的周长为24，AC的垂直平分线交BC于点D，垂足为E，若AE＝3，则△ADB的周长是 ．
16．（4分）如图，△ABC中，AB＝AC，∠B＝40°，点D是BC上一动点，将△ABD沿AD折叠得到△ADE，当△ADE与△ABC重叠部分是直角三角形时，∠BAD的度数为 ．
三、解答题（本大题共有8小题，共66分）
17．（8分）解不等式（组），把解集在数轴上表示出来．
（1）3﹣x＜2x+6；
（2）．
18．（6分）如图，在正方形网格中，点A、B、C、M、N都在格点上．
（1）作△ABC关于直线MN对称的图形△A′B′C′；
（2）在直线MN上找一点P，使PA+PC的值最小，标出点P的位置（保留作图痕迹）．
19．（6分）如图，在四边形ABCD中，∠A＝90°，AD＝AB＝4，BC＝6，CD＝2，求∠ADC的度数．
20．（6分）2如图，AB＝AE，∠B＝∠E，∠BCA＝∠EDA，AF⊥CD．
（1）求证：△ABC≌△AED；
（2）试说明∠BAF与∠EAF的数量关系．
21．（8分）如图，在△ABC中，AE是边BC上的高．
（1）若AD是∠BAC的平分线，∠B＝40°，∠C＝50°，求∠DAE的度数；
（2）若AD是BC边上的中线，，，求S△AEC．
22．（10分）某电器超市销售A、B两种型号的电风扇，A型号每台进价为200元，B型号每台进价为150元，下表是近两天的销售情况：
（进价、售价均保持不变，利润＝销售收入﹣进货成本）
（1）求A、B两种型号的电风扇的销售单价；
（2）若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台，求A种型号的电风扇最多能采购多少台？
（3）在（2）的条件下，超市销售完这30台电风扇能否实现利润不少于1060元的目标？若能，请给出相应的采购方案；若不能，请说明理由．
23．（10分）对m、n定义一种新运算“⊗”，规定：m⊗n＝am﹣bn+5．（a，b均为非零常数），等式右边的运算是通常的四则运算，例如：5⊗6＝5a﹣6b+5．
（1）已知2⊗3＝1，3⊗（﹣1）＝10．
①求a、b的值；
②若关于x的不等式组有且只有两个整数解，求字母t的取值范围；
（2）若运算“⊗”满足加法交换律，即对于我们所学过的任意数m、n，结论“m⊗n＝n⊗m”都成立，试探究a、b应满足的关系．
24．（12分）如图1，△ABC和△CDE均为等腰三角形，AC＝BC，CD＝CE，AC＞CD，∠ACB＝∠DCE＝α，且点A、D、E在同一直线上，连接BE．
（1）求证：AD＝BE．
（2）如图2，若α＝90°，CM⊥AE于M．若CM＝7，BE＝10，试求AB的长．
（3）如图3，若α＝120°，CM⊥AE于M，BN⊥AE于N，，CM＝b，直接写出AE的值（用a，b的代数式表示）．
2024-2025学年浙江省宁波市余姚市子陵教育集团八年级（上）期中数学试卷
参考答案与试题解析
一、选择题（本大题有10小题，每小题3分，共30分）
1．（3分）下面四个图形分别是节能、节水、低碳和绿色食品标志，在这四个标志中，是轴对称图形的是（ ）
A．B．C．D．
【分析】根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．
【解答】解：选项A、C、D的图形不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形．
选项B的图形能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形．
故选：B．
2．（3分）若a＜b，则下列不等式中成立的是（ ）
A．a﹣3＞b﹣3B．a+3＞b+3C．﹣3a＞﹣3bD．
【分析】根据不等式的性质进行分析判断．
【解答】解：A、在不等式a＜b的两边都减3，不等号的方向不变，即a+1＞b+1，原变形错误，故本选项不符合题意；
B、在不等式a＜b的两边同时都加3，不等号的方向不变，即a+3＜b+3，原变形错误，故本选项不符合题意；
C、在不等式a＜b的两边同时乘以﹣3，不等号的方向改变，即﹣3a＞﹣3b，原变形正确，故本选项符合题意；
D、在不等式a＜b的两边同时乘以，不等号的方向不变，即，原变形错误，故本选项不符合题意；
故选：C．
3．（3分）等腰三角形的底角等于50°，则这个等腰三角形顶角的度数是（ ）
A．50°B．65°C．80°D．100°
【分析】根据等腰三角形的性质和三角形内角和定理即可确定．
【解答】解：∵等腰三角形的底角等于50°，
∴180°﹣50°﹣50°＝80°，
∴等腰三角形的顶角为80°，
故选：C．
4．（3分）如图，点E、H、G、N共线，∠E＝∠N，EF＝NM，添加一个条件，不能判断△EFG≌△NMH的是（ ）
A．EH＝NGB．∠F＝∠MC．FG＝MHD．FG∥HM
【分析】根据三角形全等的判定方法即可求解．
【解答】解：在△EFG与△NMH中，已知，∠E＝∠N，EF＝NM，
A．由EH＝NG可得EG＝NH，所以添加条件EH＝NG，根据SAS可证△EFG≌△NMH，故本选项不符合题意；
B．添加条件∠F＝∠M，根据ASA可证△EFG≌△NMH，故本选项不符合题意；
C．添加条件FG＝MH，不能证明△EFG≌△NMH，故本选项符合题意；
D．由FG∥HM可得∠EGF＝∠NHM，所以添加条件FG∥HM，根据AAS可证△EFG≌△NMH，故本选项不符合题意；
故选：C．
5．（3分）如图，△ABC中，D为AB中点，E在AC上，且BE⊥AC．若DE＝5，AE＝8，则BE的长度是（ ）
A．5B．5.5C．6D．6.5
【分析】根据直角三角形斜边上的中线求出AB长，根据勾股定理求出BE即可．
【解答】解：∵BE⊥AC，
∴∠BEA＝90°，
∵DE＝5，D为AB中点，
∴AB＝2DE＝10，
∵AE＝8，
∴由勾股定理得：BE＝＝6，
故选：C．
6．（3分）给出下列命题：①三角形任何两边之和大于第三边；②三角形任何一外角等于两内角之和；③两边和一角对应相等的两个三角形全等，下列属于真命题的是（ ）
A．①③B．②③C．①②D．①
【分析】利用三角形的三边关系、外角的性质、全等三角形的判定方法等知识分别判断后即可确定正确的选项．
【解答】解：①三角形任何两边之和大于第三边，正确，是真命题，符合题意；
②三角形任何一外角等于不相邻的两内角之和，故原命题错误，是假命题，不符合题意；
③两边和夹角对应相等的两个三角形全等，故原命题错误，是假命题，不符合题意．
真命题有①，
故选：D．
7．（3分）如图，在△ABC中，∠ACB为钝角．用直尺和圆规在边AB上确定一点D．使∠ADC＝2∠B，则符合要求的作图痕迹是（ ）
A．B．
C．D．
【分析】由∠ADC＝2∠B且∠ADC＝∠B+∠BCD知∠B＝∠BCD，据此得DB＝DC，由线段的中垂线的性质可得答案．
【解答】解：∵∠ADC＝2∠B且∠ADC＝∠B+∠BCD，
∴∠B＝∠BCD，
∴DB＝DC，
∴点D是线段BC中垂线与AB的交点，
故选：B．
8．（3分）若一个直角三角形的两边长分别为3和4，则它的第三边长为（ ）
A．5B．C．5或4D．5或
【分析】分为两种情况：①斜边是4有一条直角边是3，②3和4都是直角边，根据勾股定理求出即可．
【解答】解：分为两种情况：①斜边是4有一条直角边是3，由勾股定理得：第三边长是＝；
②3和4都是直角边，由勾股定理得：第三边长是＝5；
即第三边长是5或，
故选：D．
9．（3分）如图，在矩形ABCD中，BC＝6，CD＝3，将△BCD沿对角线BD翻折，点C落在点C′处，BC′交AD于点E，则线段DE的长为（ ）
A．3B．C．5D．
【分析】首先根据题意得到BE＝DE，然后根据勾股定理得到关于线段AB、AE、BE的方程，解方程即可解决问题．
【解答】解：设ED＝x，则AE＝6﹣x，
∵四边形ABCD为矩形，
∴AD∥BC，
∴∠EDB＝∠DBC；
由题意得：∠EBD＝∠DBC，
∴∠EDB＝∠EBD，
∴EB＝ED＝x；
由勾股定理得：
BE2＝AB2+AE2，
即x2＝9+（6﹣x）2，
解得：x＝3.75，
∴ED＝3.75．
故选：B．
10．（3分）如图，点P是∠AOB内任意一点，且∠AOB＝40°，点M和点N分别是射线OA和射线OB上的动点，当△PMN周长取最小值时，则∠MPN的度数为（ ）
A．140°B．100°C．50°D．40°
【分析】分别作点P关于OA、OB的对称点P1、P2，连P1、P2，交OA于M，交OB于N，△PMN的周长＝P1P2，然后得到等腰△OP1P2中，∠OP1P2+∠OP2P1＝100°，即可得出∠MPN＝∠OPM+∠OPN＝∠OP1M+∠OP2N＝100°．
【解答】解：分别作点P关于OA、OB的对称点P1、P2，连接P1P2，交OA于M，交OB于N，则
OP1＝OP＝OP2，∠OP1M＝∠MPO，∠NPO＝∠NP2O，
根据轴对称的性质，可得MP＝P1M，PN＝P2N，则
△PMN的周长的最小值＝P1P2，
∴∠P1OP2＝2∠AOB＝80°，
∴等腰△OP1P2中，∠OP1P2+∠OP2P1＝100°，
∴∠MPN＝∠OPM+∠OPN＝∠OP1M+∠OP2N＝100°，
故选：B．
二、填空题（本大题有6小题，每小题4分，共24分）
11．（4分）“x的3倍与y的差是负数”用不等式表示为 3x﹣y＜0 ．
【分析】根据用字母表示数或数量关系及书写规程即可求解．
【解答】解：x的3倍表示为3x，
∴根据题意得，3x﹣y＜0，
故答案为：3x﹣y＜0．
12．（4分）已知三角形的三边长分别为3，5，x，若x是整数，则x的值可取 3（答案不唯一） （只填一个）．
【分析】根据三角形的三边关系解答即可．
【解答】解：由三角形三边关系定理得5﹣3＜x＜5+3，即2＜x＜8．
∵x是整数，
∴x可以取3．
故答案为：3（答案不唯一）．
13．（4分）“内错角相等，两直线平行”的逆命题是 两直线平行，内错角相等 ．
【分析】把一个命题的条件和结论互换就得到它的逆命题．
【解答】解：“内错角相等，两直线平行”的条件是：内错角相等，结论是：两直线平行．
将条件和结论互换得逆命题为：两条直线平行，内错角相等．
故答案为：两直线平行，内错角相等．
14．（4分）在△ABC中，∠A，∠B，∠C的对边分别是a，b，c，且满足（a﹣b）2+|b﹣c|2＝0，则△ABC是 等边 三角形．
【分析】根据非负数的性质求出a﹣b＝0，且b﹣c＝0，进而判断出△ABC的形状．
【解答】解：∵（a﹣b）2+|b﹣c|2|＝0，
∴a﹣b＝0，且b﹣c＝0，
∴a＝b＝c，
∴△ABC是等边三角形，
故答案为：等边．
15．（4分）如图，△ABC的周长为24，AC的垂直平分线交BC于点D，垂足为E，若AE＝3，则△ADB的周长是 18 ．
【分析】根据线段垂直平分线得出AD＝DC，AC＝2AE＝8，根据△ABC的周长求出AB+BC＝16，求出△ABD的周长＝AB+BC，代入求出即可．
【解答】解：∵AC的垂直平分线交BC于点D，垂足为E，AE＝3，
∴AD＝DC，AC＝2AE＝6，
∵△ABC的周长为24，
∴AB+BC+AC＝24，
∴AB+BC＝24﹣6＝18，
∴△ADB的周长是AB+AD+BD＝AB+CD+BD＝AB+BC＝18，
故答案为：18．
16．（4分）如图，△ABC中，AB＝AC，∠B＝40°，点D是BC上一动点，将△ABD沿AD折叠得到△ADE，当△ADE与△ABC重叠部分是直角三角形时，∠BAD的度数为 25°或50°或75° ．
【分析】分三种情况：当∠ADC＝90°时；当∠AFD＝90°时；当∠AHD＝90°时；分别求解即可得出答案．
【解答】解：如图，当∠ADC＝90°时，
，
∵∠B＝40°，
∴∠BAD＝90°﹣∠B＝90°﹣40°＝50°；
如图，当∠AFD＝90°时，
，
由折叠的性质可得：△ABD≌△AED，∠BAD＝∠EAD，
∵∠B＝40°，
∴∠BAF＝90°﹣∠B＝50°，
∴；
如图，当∠AHD＝90°时，
，
由折叠的性质可得：∠B＝∠E＝40°，∠ADB＝∠ADE，
∵AB＝AC，
∴∠B＝∠C＝40°，
∴∠HDC＝90°﹣∠C＝50°，
∴，
∴∠BAD＝180°﹣∠B﹣∠ADB＝75°；
综上所述，∠BAD的度数为25°或50°或75°，
故答案为：25°或50°或75°．
三、解答题（本大题共有8小题，共66分）
17．（8分）解不等式（组），把解集在数轴上表示出来．
（1）3﹣x＜2x+6；
（2）．
【分析】（1）根据移项、合并同类项、系数化为1的步骤求出不等式的解集，然后根据在数轴上表示不等式解集的方法画出数轴即可；
（2）分别求出不等式组中两个不等式的解集，进而得到不等式组的解集，然后根据在数轴上表示不等式解集的方法画出数轴即可．
【解答】解：（1）移项得：﹣x﹣2x＜6﹣3，
合并同类项得：﹣3x＜3，
系数化为1得：x＞﹣1，
在数轴上表示解集为：
（2），
解不等式①得：x＜3，
解不等式②得：x≥﹣1，
所以不等式组的解集为：﹣1≤x＜3，
在数轴上表示解集为：
18．（6分）如图，在正方形网格中，点A、B、C、M、N都在格点上．
（1）作△ABC关于直线MN对称的图形△A′B′C′；
（2）在直线MN上找一点P，使PA+PC的值最小，标出点P的位置（保留作图痕迹）．
【分析】（1）利用轴对称的性质分别作出A，B，C的对应点A1，B1，C1即可；
（2）连接A1C交直线MN于点P，可得A1P＝AP，即得△PAC的周长＝AP+CP+AC＝A1P+CP+AC＝A1P+AC，根据两点之间线段最短可知此时△PAC的周长最小，故点P即为所求．
【解答】解：（1）如图所示，即为所求；
（2）如图所示，点P即为所求．
19．（6分）如图，在四边形ABCD中，∠A＝90°，AD＝AB＝4，BC＝6，CD＝2，求∠ADC的度数．
【分析】连接BD，根据勾股定理求出BD，根据勾股定理的逆定理判断∠CDB＝90°，计算即可．
【解答】解：连接BD，
∵∠A＝90°，AD＝AB＝4，
∴∠ADB＝45°，
在Rt△ADB中，BD2＝AD2+AB2＝16+16＝32，
在△CDB中，CB2﹣DC2＝62﹣22＝32，
∴CB2﹣DC2＝BD2，
∴∠CDB＝90°，
∴∠ADC＝∠ADB+∠CDB＝135°．
20．（6分）2如图，AB＝AE，∠B＝∠E，∠BCA＝∠EDA，AF⊥CD．
（1）求证：△ABC≌△AED；
（2）试说明∠BAF与∠EAF的数量关系．
【分析】（1）根据AAS即可证明△ABC≌△AED；
（2）根据全等三角形的性质得出AC＝AD，∠BAC＝∠EAD，运用等腰三角形性质及角的和差解答问题．
【解答】（1）证明：在△ABC和△AED中，
，
∴△ABC≌△AED（AAS）；
（2）解：∠BAF＝∠EAF，理由如下：
∵△ABC≌△AED，
∴AC＝AD，∠BAC＝∠EAD，
∵AF⊥CD，
∴∠CAF＝∠DAF，
∴∠BAC+∠CAF＝∠EAD+∠DAF，
∴∠BAF＝∠EAF．
21．（8分）如图，在△ABC中，AE是边BC上的高．
（1）若AD是∠BAC的平分线，∠B＝40°，∠C＝50°，求∠DAE的度数；
（2）若AD是BC边上的中线，，，求S△AEC．
【分析】（1）利用三角形内角和先求∠BAC，再用外角性质和直角三角形性质求出∠DAE；
（2）利用三角形中线定义及三角形面积公式求解即可．
【解答】解：（1）∵∠B＝40°，∠C＝50°，
∴∠BAC＝180°﹣∠B﹣∠C＝180°﹣40°﹣50°＝90°，
∵AD平分∠BAC，
∴∠BAD＝∠BAC＝45°，
∴∠ADE＝∠B+∠BAD＝85°，
∵AE是边BC上的高，
∴∠DAE+∠ADE＝90°，
∴∠DAE＝5°．
（2）∵AD是BC边上的中线，，
∴S△ABD＝S△ACD＝6cm2，
∵，S△ACD＝S△ADE+S△AEC，
∴S△AEC＝4cm2．
22．（10分）某电器超市销售A、B两种型号的电风扇，A型号每台进价为200元，B型号每台进价为150元，下表是近两天的销售情况：
（进价、售价均保持不变，利润＝销售收入﹣进货成本）
（1）求A、B两种型号的电风扇的销售单价；
（2）若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台，求A种型号的电风扇最多能采购多少台？
（3）在（2）的条件下，超市销售完这30台电风扇能否实现利润不少于1060元的目标？若能，请给出相应的采购方案；若不能，请说明理由．
【分析】（1）设A种型号电风扇的销售单价为x元，B种型号电风扇的销售单价为y元，根据近两天的销售情况表，即可得出关于x，y的二元一次方程组，解之即可得出结论；
（2）设采购A种型号电风扇a台，则采购B种型号电风扇（30﹣a）台，根据总价＝单价×数量结合总价不超过5400元，即可得出关于a的一元一次不等式，解之取其中的最大值即可得出结论；
（3）根据总利润＝每台利润×数量结合总利润不少于1060元，即可得出关于a的一元一次不等式，解之即可得出a的取值范围，结合（2）的结论及a为整数，即可得出各采购方案．
【解答】解：（1）设A种型号电风扇的销售单价为x元，B种型号电风扇的销售单价为y元，
依题意，得：，
解得：．
答：A种型号电风扇的销售单价为240元，B种型号电风扇的销售单价为180元．
（2）设采购A种型号电风扇a台，则采购B种型号电风扇（30﹣a）台，
依题意，得：200a+150（30﹣a）≤5400，
解得：a≤18．
答：A种型号的电风扇最多能采购18台．
（3）依题意，得：（240﹣200）a+（180﹣150）（30﹣a）≥1060，
解得：a≥16．
∵a≤18，
∴16≤a≤18．
∵a为整数，
∴a＝16，17，18．
∴共有三种采购方案，方案1：采购A种型号电风扇16台，B种型号电风扇14台；方案2：采购A种型号电风扇17台，B种型号电风扇13台；方案3：采购A种型号电风扇18台，B种型号电风扇12台．
23．（10分）对m、n定义一种新运算“⊗”，规定：m⊗n＝am﹣bn+5．（a，b均为非零常数），等式右边的运算是通常的四则运算，例如：5⊗6＝5a﹣6b+5．
（1）已知2⊗3＝1，3⊗（﹣1）＝10．
①求a、b的值；
②若关于x的不等式组有且只有两个整数解，求字母t的取值范围；
（2）若运算“⊗”满足加法交换律，即对于我们所学过的任意数m、n，结论“m⊗n＝n⊗m”都成立，试探究a、b应满足的关系．
【分析】（1）①依据题意，由2⊗3＝1，3⊗（﹣1）＝10，可得，进而计算可以得解；
②依据题意，结合（1）可得，，即，又不等式组有且只有两个整数解，从而可得2≤＜3，进而计算可以得解；
（2）依据题意，由m⊗n＝n⊗m，从而ma﹣nb+5＝na﹣mb+5，变形为（a+b）（m﹣n）＝0，又m，n为任意数，故m﹣n不一定等于0，进而可得a+b＝0，即可得解．
【解答】解：（1）①由题意，∵2⊗3＝1，3⊗（﹣1）＝10，
∴可得方程组．
∴解得．
∴a＝1，b＝2．
②由题意，∵a＝1，b＝2，
∴不等式组可化为．
∴．
又∵上面的不等式组有且只有两个整数解，
∴2≤＜3．
∴23≤t＜26．
（2）由m⊗n＝n⊗m，
∴ma﹣nb+5＝na﹣mb+5．
∴ma﹣nb﹣na+mb＝0．
∴m（a+b）﹣n（a+b）＝0．
∴（a+b）（m﹣n）＝0．
又∵m，n为任意数，
∴（m﹣n）不一定等于0．
∴a+b＝0．
24．（12分）如图1，△ABC和△CDE均为等腰三角形，AC＝BC，CD＝CE，AC＞CD，∠ACB＝∠DCE＝α，且点A、D、E在同一直线上，连接BE．
（1）求证：AD＝BE．
（2）如图2，若α＝90°，CM⊥AE于M．若CM＝7，BE＝10，试求AB的长．
（3）如图3，若α＝120°，CM⊥AE于M，BN⊥AE于N，，CM＝b，直接写出AE的值（用a，b的代数式表示）．
【分析】（1）证明△ACD≌△BCE（SAS），即可得出AD＝BE；
（2）设AE交BC于点H，由全等三角形的性质得出∠CAD＝∠CBE，AD＝BE＝10，证出∠AEB＝∠ACH＝90°，△CDE是等腰直角三角形，得出CM＝DM＝ME＝7，得出DE＝2CM＝14，求出AE＝24，由勾股定理即可得出答案；
（3）由等腰三角形的性质和三角形内角和定理得出∠CDM＝∠CEM＝30°．∠CMD＝90°，DM＝EM．由直角三角形的性质求出DE＝2DM＝2b．BE＝2a．即可得出答案．
【解答】（1）证明：∵∠ACB＝∠DCE，
∴∠ACB﹣∠DCB＝∠DCE﹣∠DCB，
∴∠ACD＝∠BCE，
在△ACD和△BCE中，
，
∴△ACD≌△BCE（SAS），
∴AD＝BE；
（2）解：设AE交BC于点H，如图2，
由（1）得：△ACD≌△BCE，
∴∠CAD＝∠CBE，AD＝BE＝10，
∵∠AHC＝∠BHE，
∴∠AEB＝∠ACH＝90°，
∵∠ACB＝∠DCE＝α＝90°，CD＝CE，
∴△CDE是等腰直角三角形，
∵CM⊥DE，
∴CM＝DM＝ME＝7，
∴DE＝2CM＝14，
∵AE＝AD+DE＝10+14＝24，∠AEB＝90°，
∴AB＝＝＝26；
（3）解：AE＝2a+2b；理由如下：
∵△ACB和△DCE均为等腰三角形，且∠ACB＝∠DCE＝120°，
∴∠CDM＝∠CEM＝×（180°﹣120°）＝30°．
∵CM⊥DE，
∴∠CMD＝90°，DM＝EM．
在Rt△CMD中，∠CMD＝90°，∠CDM＝30°，
∴CD＝2CM＝2b，
∴DM＝＝＝b，
∴DE＝2DM＝2b．
∵∠BEC＝∠ADC＝180°﹣30°＝150°，∠BEC＝∠CEM+∠AEB，
∴∠AEB＝∠BEC﹣∠CEM＝150°﹣30°＝120°，
∴∠BEN＝180°﹣120°＝60°．
在Rt△BNE中，∠BNE＝90°，∠BEN＝60°，
∴∠NBE＝90°﹣∠BEN＝30°，
∴BE＝2NE，
∴BN＝＝NE＝a，
∴NE＝a，
∴BE＝2a．
∵AD＝BE，AE＝AD+DE，
∴AE＝BE+DE＝2a+2b．销售时段
销售数量
销售收入
A种型号
B种型号
第一天
3台
5台
1620元
第二天
4台
10台
2760元
销售时段
销售数量
销售收入
A种型号
B种型号
第一天
3台
5台
1620元
第二天
4台
10台
2760元