湖北省鄂北六校（宜城一中、枣阳一中等）2024-2025学年高三上学期期中考试数学试卷（Word版附解析）

这是一份湖北省鄂北六校（宜城一中、枣阳一中等）2024-2025学年高三上学期期中考试数学试卷（Word版附解析），文件包含湖北省鄂北六校宜城一中枣阳一中等2024-2025学年高三上学期期中考试数学试题Word版含解析docx、湖北省鄂北六校宜城一中枣阳一中等2024-2025学年高三上学期期中考试数学试题Word版无答案docx等2份试卷配套教学资源，其中试卷共23页， 欢迎下载使用。

2024—2025学年上学期期中考试
高三数学试题
时间：120分钟 主命题学校：曾都一中
分值：150分 命题老师：姜华红 徐士勇 董建勇
注意事项：
1.答题前，先将自己的姓名、准考证号、考场号、座位号填写在试卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置.
2.选择题的作答：每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑.写在试卷、草稿纸和答题卡上的非答题区域均无效.
3.非选择题的作答：用黑色签字笔直接答在答题卡上对应的答题区域内.写在试卷、草稿纸和答题卡上的非答题区域均无效.
一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一个选项是正确的.请把正确的选项填涂在答题卡相应的位置上.
1. 已知集合，，则（ ）
A. B. C. D.
2. 若，则（ ）
A. B. C. D.
3. 已知x，y是任意实数，则是且的（ ）
A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件
4. 设均为非零向量，且，，则与的夹角为（ ）
A. B. C. D.
5. 若，，，则a，b，c的大小关系为（ ）.
A. B. C. D.
6. 已知等比数列的前3项和为28，且，则（ ）
A. 28B. 56C. 64D. 128
7. 已知，，，则（ ）
A. B. C. D.
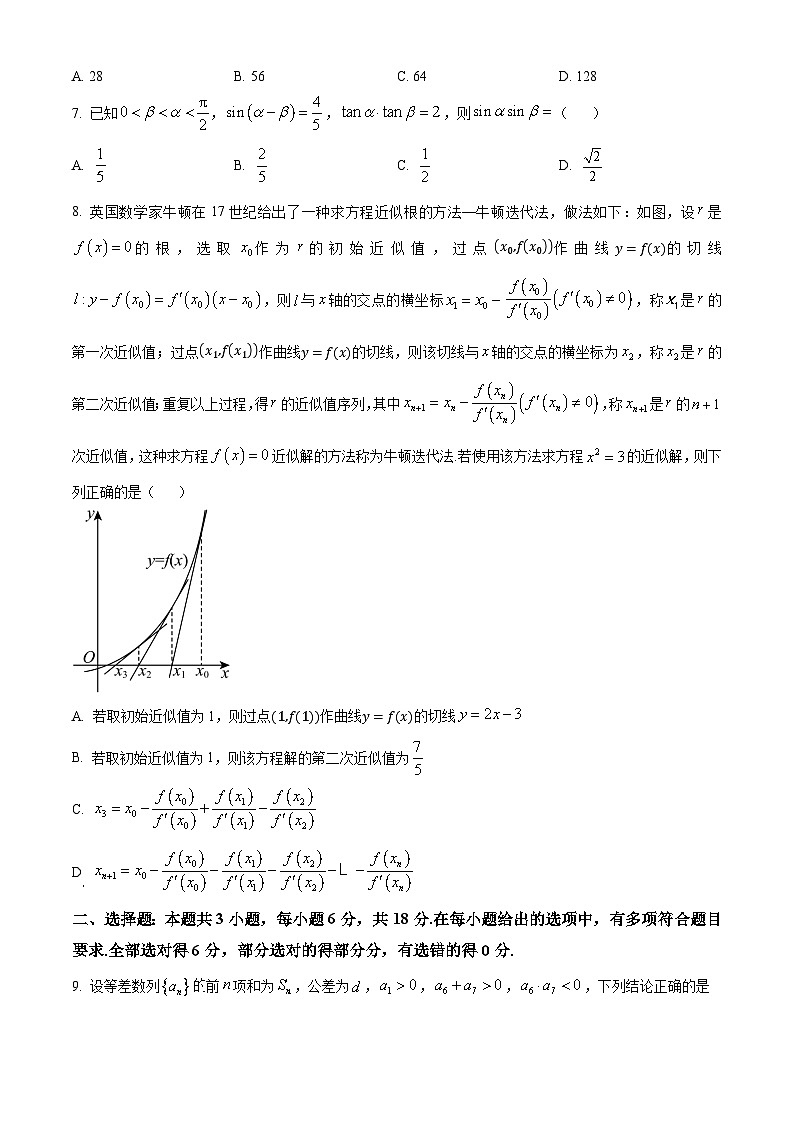
8. 英国数学家牛顿在17世纪给出了一种求方程近似根的方法—牛顿迭代法，做法如下：如图，设是的根，选取作为的初始近似值，过点x0,fx0作曲线y=fx的切线，则与轴的交点的横坐标，称是的第一次近似值；过点x1,fx1作曲线y=fx的切线，则该切线与轴的交点的横坐标为，称是的第二次近似值；重复以上过程，得的近似值序列，其中，称是的次近似值，这种求方程近似解的方法称为牛顿迭代法.若使用该方法求方程的近似解，则下列正确的是（ ）

A. 若取初始近似值为1，则过点1,f1作曲线y=fx的切线
B. 若取初始近似值为1，则该方程解的第二次近似值为
C.
D
二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对得6分，部分选对的得部分分，有选错的得0分.
9. 设等差数列前项和为，公差为，，，，下列结论正确的是( ).
A ，B. C. D. 当时，最大
10. 已知实数满足，则下列结论正确的是（ ）
A. 的最小值为9B. 的最大值为
C. 的最大值为D. 的最小值为
11. 函数的图象过原点，且无限接近直线但又不与该直线相交，则下列结论正确的是（ ）
A.
B.
C 若，则
D. 方程有3个实数根
三、填空题：本大题共3小题，每小题5分，共15分.
12. 已知函数y=fx，x∈R，且，，， ，，，则______.
13. 如图，函数的部分图象如图所示，已知点A，D为的零点，点B，C为的极值点，，则______.

14. 若，，记数列的前项和为，则的最小值为______.
四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知函数.
（1）求的单调减区间；
（2）将函数y=fx的图象向左平移个单位长度，再将所得图象上各点的横坐标变为原来的2倍（纵坐标不变），得到函数y=gx的图象.若对任意，，求实数的最小值.
16. 已知函数在点处的切线方程为
（1）求函数的解析式；
（2）若，且过点可作曲线的三条切线，求实数的取值范围.
17. 在中，角，，所对边分别为，，，且
（1）求角的大小；
（2）设是边AC上一点，BD为角平分线且，求的值.
18. 已知函数.
（1）若，求极值；
（2）求函数的单调区间；
（3）若函数有两个极值点，，求证：.
19. 把满足任意，总有的函数称为“类余弦型”函数.
（1）已知为“类余弦型”函数，，求f1的值；
（2）在（1）的条件下，定义数列：，求的值；
（3）若为“类余弦型”函数，且g0>0，对任意非零实数，总有gt>1.设有理数，满足，判断与的大小关系，并给出证明.