陕西省西安市长安区2024-2025学年上学期九年级期中数学试题

这是一份陕西省西安市长安区2024-2025学年上学期九年级期中数学试题，共9页。试卷主要包含了本试卷分为第一部分等内容，欢迎下载使用。
注意事项：
1．本试卷分为第一部分（选择题）和第二部分（非选择题）。全卷共4页，总分120分。考试时间120分钟。
2．领到试卷和答题卡后，请用0.5毫米黑色墨水签字笔，分别在试卷和答题卡上填写姓名和准考证号。
3．请在答题卡上各题的指定区域内作答，否则作答无效。
4．作图时，先用铅笔作图，再用规定签字笔描黑。
5．考试结束，本试卷和答题卡一并交回。
第一部分（选择题共30分）
一、选择题（共10小题，每小题3分，计30分．每小题只有一个选项是符合题意的）
1．从长度分别为3，5，7，10的四根小木棒中任选三根，能构成三角形的概率为（ ）
A．B．C．D．
2．如图，某同学用带有刻度的直尺在数轴上作图，若图中的虚线互相平行，则点P表示的数是（ ）
（第2题图）
A．1B．C．D．5
3．下面四条线段a，b，c，d是成比例线段的是（ ）
A．，，，B．，，，
C．，，，D．，，，
4．将方程化成的形式，则的值为（ ）
A．－6B．－4C．0D．2
5．如图，已知，则下列说法不正确的是（ ）
（第5题图）
A．当时，是矩形B．当时，是菱形
C．当时，是正方形D．当时，是菱形
6．若m、n是关于x的一元二次方程的两根，则的值为（ ）
A．－5B．－3C．－2D．－1
7．甲乙两个不透明的袋子中分别装有除标记数字外完全相同的卡片，甲袋内装有4张卡片分别标记数字1、2、3、4，乙袋内装有3张卡片分别标记数字2、3、4．小红从两袋中各取出一张卡片，其数字和大于6的概率为（ ）
A．B．C．D．
8．某水果批发商以每千克5元的价格对外批发红富士苹果，为了减少库存，决定对苹果降价销售，经过两次降价后，批发价为每千克3.6元．设平均每次降价的百分率为x，则可列方程为（ ）
A．B．C．D．
9．如图，在菱形ABCD中摆放了一副三角板，等腰直角三角板DEF的一条直角边DE在菱形边AD上，直角顶点E为AD的中点，含30°角的直角三角板的斜边GB在菱形ABCD的边AB上，此时两三角板直角边恰好紧贴在一起，连接AC，若，则AC的长为（ ）
（第9题图）
A．8B．C．D．
10．如图，在正方形ABCD中，边长为2的等边的顶点E、F分别在BC和CD上，下列结论：①；②；③；④；⑤．其中正确的个数为（ ）
（第10题图）
A．5B．4C．3D．2
第二部分（非选择题共90分）
二、填空题（共8小题，每小题3分，计24分）
11．若关于x的方程的一个根是，则k的值是______．
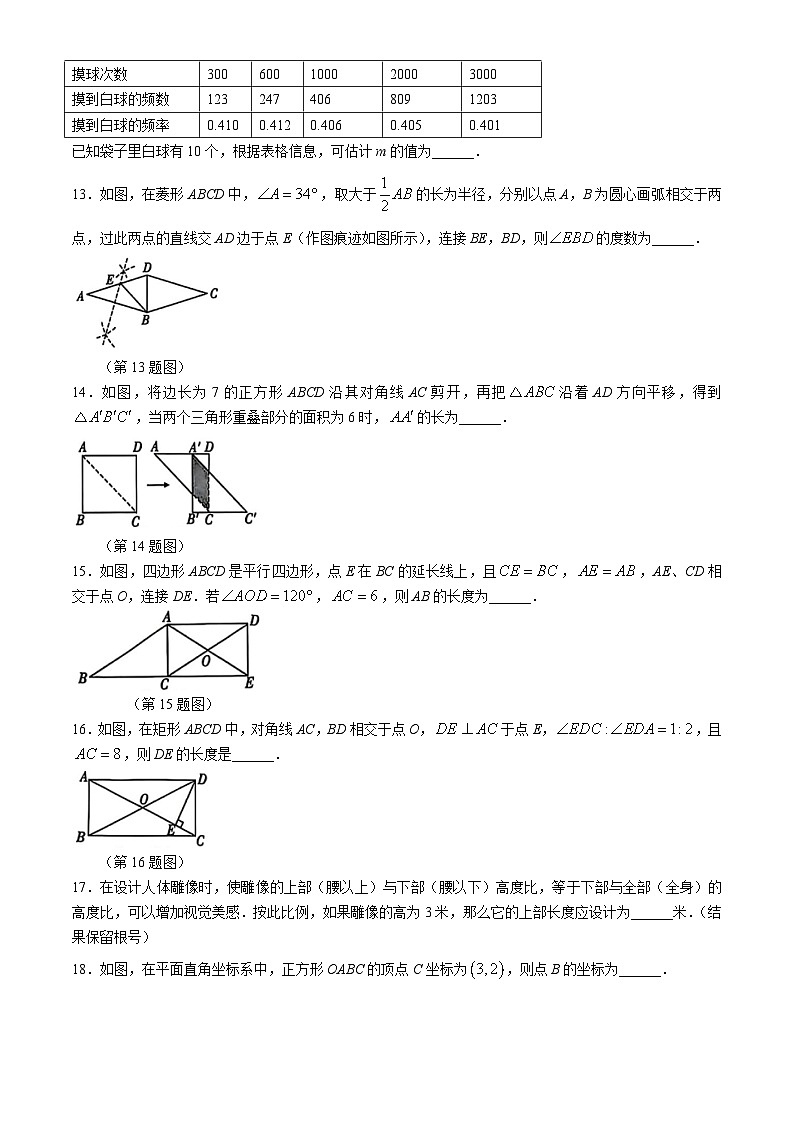
12．一个不透明的袋子里装有红球和白球共m个，它们除颜色外完全相同，每次搅匀后从中随机摸出一个球并记下颜色，再放回袋中，不断重复，统计汇总数据如下表：
已知袋子里白球有10个，根据表格信息，可估计m的值为______．
13．如图，在菱形ABCD中，，取大于的长为半径，分别以点A，B为圆心画弧相交于两点，过此两点的直线交AD边于点E（作图痕迹如图所示），连接BE，BD，则的度数为______．
（第13题图）
14．如图，将边长为7的正方形ABCD沿其对角线AC剪开，再把沿着AD方向平移，得到，当两个三角形重叠部分的面积为6时，的长为______．
（第14题图）
15．如图，四边形ABCD是平行四边形，点E在BC的延长线上，且，，AE、CD相交于点O，连接DE．若，，则AB的长度为______．
（第15题图）
16．如图，在矩形ABCD中，对角线AC，BD相交于点O，于点E，，且，则DE的长度是______．
（第16题图）
17．在设计人体雕像时，使雕像的上部（腰以上）与下部（腰以下）高度比，等于下部与全部（全身）的高度比，可以增加视觉美感．按此比例，如果雕像的高为3米，那么它的上部长度应设计为______米．（结果保留根号）
18．如图，在平面直角坐标系中，正方形OABC的顶点C坐标为，则点B的坐标为______．
（第18题图）
三、解答题（共8小题，共66分）
19．（本小题12分）解方程：
（1）；（2）；
（3）（用配方法）；（4）．
20．（本小题6分）已知．
（1）如果，求a的值；
（2）求代数式的值．
21．（本小题6分）用图中两个可自由转动的转盘做“配紫色”游戏（其中一个转出红色，另一个转出蓝色即可配成紫色），其中A转盘被分成相等的六个扇形，B转盘被分成相等的三个扇形．
（第21题图）
（1）求转动A转盘，指针指向蓝色的概率；
（2）同时转动两个转盘，求转盘停止时指针所指的颜色可配成紫色的概率．
22．（本小题7分）已知a、b、c是等腰的三边长，其中，b和c是关于x的方程的两根，求m的值及的周长．
23．（本小题8分）如图，的对角线AC、BD相交于点O，AC平分，过点D作，过点C作，DP、CP交于点P，连接OP．
（第23题图）
（1）求证：四边形ABCD是菱形；
（2）若，，求OP的长．
24．（本小题8分）某民宿有60间客房供游客居住，在旅游旺季，当客房的定价为每天150元时，所有客房都可以住满，根据以往经验，客房定价每提高10元，就会有1间客房空闲．
（1）若客房定价提高20元，求该民宿每天收入；
（2）若该民宿希望每天收入为11000元且能吸引更多的游客，则每间客房的定价应为多少元？
25．（本小题9分）如图，四边形ABCD是正方形，点G为边CD上一点，连接AG并延长，交BC的延长线于点F，连接BD交AF于点E，连接EC．
（第25题图）
（1）求证：；
（2）求证：；
（3）已知，求的值．
26．（本小题10分）如图，在中，，，cm，点D以4cm/秒的速度从点C出发沿CA向A点运动，同时点E以2cm/秒的速度从点A出发沿AB向B点运动，当其中一个点到达终点时，另一个点也随之停止运动．过点D作于点F，连接DE，EF，设运动的时间为t秒．
（第26题图）
（1）当t为何值时，四边形ADFE为菱形？
（2）当t为何值时，的面积为cm2？
（3）当t为何值时，以A、D、E为顶点的三角形与相似？
2024～2025学年度第一学期期中学习评价
九年级数学纸笔测试参考答案及评分标准
一、选择题（共10小题，每小题3分，计30分．每小题只有一个选项是符合题意的）
1．A 2．D 3．C 4．B 5．C 6．B 7．C 8．A 9．D 10．B
二、填空题（每小题3分，共24分）
11． 12．25 13．39° 14．1或6（只填一个且正确2分）
15．12 16． 17． 18．
三、解答题（共8小题，共66分）
19．解：（1）两边开平方得：，
即或，
∴，．
（2）方程可化为：，
或，
∴，．
（3）方程可化为：，
，，
∴，．
（4）方程可化为：，即，
这里，，．
∵，
∴，
∴，．
20．解：（1）∵，∴，
∴，即．
（2）∵，∴，
∴．
∵，∴，∴，
∴．
21．解：（1）转动A转盘，指针指向蓝色的概率为．
（2）列表为：
共有18种等可能的结果数，其中一个转出红色另一个转出蓝色的结果数为5，
所以可配成紫色的概率为：．
22．解：（1）当a为腰长时，4是的根，
∴，∴，
即方程为，
∴，，
此时的周长为10．
当a为底边长时，方程有两个相等的根，
∴，
∴，
即方程为，∴，
此时不能构成三角形，
综上所述，的周长为10．
23．（1）证明∵四边形ABCD是平行四边形，∴．
∵AC平分，∴，
∴四边形ABCD是菱形．
（2）解：∵在菱形ABCD中，，，
∴．
∵，，∴四边形OCPD是平行四边形．
∵，∴四边形OCPD是矩形，
∴．
24．解：（1）客房定价提高20元，客房定价为每天（元），客房入住（间）
所以该民宿每天收入为：（元）．
（2）设每间客房的定价提高了x元，则客房定价为每天元，客房入住间
根据题意可列方程：，
解这个方程得：，，
所以该民宿希望每天收入为11000元且能吸引更多的游客，则每间客房的定价应为（元）．
25．（1）证明：∵四边形ABCD是正方形，∴，．
∵，∴．
（2）证明：∵，
∴．
∵四边形ABCD是正方形，∴，
∴，∴．
∵，∴．
（3）解：∵，∴，∴．
设，则，，∴，
∵，∴．
∵，∴，∴．
26．解：（1）由题意，．
∵，，cm，
∴，cm．
∵，∴，，∴，
∴四边形ADFE为平行四边形，
∴当时，四边形ADFE为菱形，
∴，即，
∴当时，四边形ADFE为菱形．
（2）由（1）知四边形ADFE为平行四边形，
∴，，
∴，
∴，，
∴，
解得：，，
∴当或时，的面积为cm2．
（3）当时，，
∴，解得：．
当时，，∴，解得：，
∴当或时，以A、D、E为顶点的三角形与相似．摸球次数
300
600
1000
2000
3000
摸到白球的频数
123
247
406
809
1203
摸到白球的频率
0.410
0.412
0.406
0.405
0.401
黄
蓝
红
红
红，黄
红，蓝
红，红
红
红，黄
红，蓝
红，红
蓝
蓝，黄
蓝，蓝
蓝，红
红
红，黄
红，蓝
红，红
黄
黄，黄
黄，蓝
黄，红
蓝
蓝，黄
蓝，蓝
蓝，红